0584

Spontaneous Muscular Activities and Estimating their Influence on Derived Diffusion Tensor Parameters

Martin Schwartz^1,2, Petros Martirosian¹, Günter Steidle¹, Bin Yang², and Fritz Schick¹
¹Section on Experimental Radiology, University Hospital of Tuebingen, Tuebingen, Germany, ²Institute of Signal Processing and System Theory, University of Stuttgart, Stuttgart, Germany

Synopsis

Estimation of diffusion tensor parameters in healthy subjects and patients suffering from neuromuscular disease can be markedly affected by a high rate of spontaneous muscular activities during the MR examination. Therefore, a concept for realistic simulation of spontaneous muscular activities in diffusion tensor imaging and the estimation of their influence on derived parameters is given in this work. The degradation of the derived parameters depends strongly on the robustness of the chosen approach for tensor estimation.

Introduction

A major issue in the measurement of diffusion tissue properties is the influence of signal outliers^1-5 as a result of spontaneous mechanical activities of resting musculature (SMAM) which are visible as signal dropouts in diffusion weighted images.^6,7 In patients suffering from neuromuscular disease, the activity rate of spontaneous muscular activities can be increased^8,9 which hampers the estimation of diffusion parameters like axial and radial diffusivity.

In this work, a new concept for realistic simulation of SMAMs in undistorted diffusion tensor imaging (DTI) data sets of the lower leg and the estimation of their influence on diffusion parameters is given by simulating SMAMs with a model-based approach. The influence on the derived diffusion parameters by applying standard approaches and a model-based preprocessing is given in dependence of the SMAM activity rate.

Methods

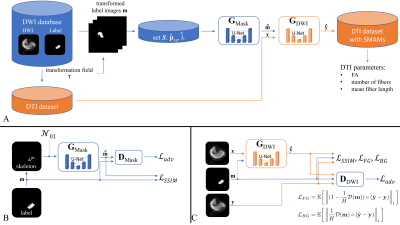
The simulation of spontaneous muscular activities in resting musculature is achieved by a model-based approach which enables the insertion of realistic signal dropouts into undistorted DTI data sets. The concept is depicted in Fig. 1A. SMAM simulation: SMAMs can be described by their activity rate, location of occurrence in the muscular region and shape. The activity rate was estimated by a Poisson distribution since fasciculations measurable in surface electromyography, which have shown high correlation to these signal dropouts⁷, can also be modelled as a Poisson distribution^10-12. The local position of the SMAMs was randomly drawn from a 2D probabilistic distribution estimated by the summation of events over time. Subsequently, the shape of the SMAMs was modelled by the two generator (G_Mask, G_DWI) networks. Diffusion weighted imaging (DWI) data from 25 healthy subjects was utilized to train two generative adversarial networks^13,14 (G_Mask, G_DWI) to generate realistic segmentation masks and natural-looking SMAMs in undistorted DTI of three healthy subjects. MR measurements were conducted on 3 T MR systems (MAGNETOM Skyra, Prisma^fit, Siemens Healthcare, Erlangen). The DWI data sets were non-rigid registered^15,16 on the three DTI data sets to transfer the SMAM masks. Only the central slice of the DTI data set was synthetically distorted due to the 2D limitation of SMAM imaging. A shallow 2D U-Net¹⁷ was utilized for both generators and a conventional convolutional encoder structure for the discriminators. A combined loss composed of a structural similarity loss¹⁸ (SSIM) and separated L1-loss (weighted with a Euclidean distance map¹⁹) was used for the preservation of the background and foreground information (Fig. 1B/C). For mask generation, a skeleton was calculated from the original mask and Gaussian noise was added to generate more random SMAM masks. 5382 paired DW images were used for training. The DWI and DTI sequence parameters are given in Fig. 2. Evaluation: The influence of SMAMs on DTI parameters was investigated by applying different diffusion tensor estimators: linear least squares (LLS)²⁰, nonlinear least squares (NLS)²¹, weighted LLS (WLLS)^22-24, robust iterative reweighted LLS (IRLLS)³ and a combination of a model-based²⁵ and cluster-based²⁶ preprocessing of the data for SMAM detection and segmentation (DL preproc. IRLLS). Following DTI parameters were calculated: fractional anisotropy (FA), axial diffusivity (AD), radial diffusivity (RD), fiber angle (θ), number of fibers and mean fiber length (MFL). Fiber tracts were calculated based on the deterministic streamline tracking^27,28 with FA <0.1 or >0.5 and angular threshold >30° as stopping criterion^29,30.

Results & Discussion

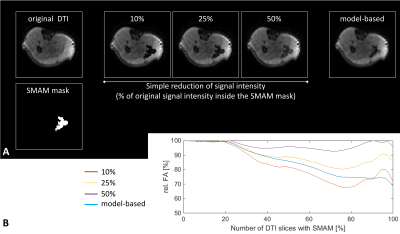
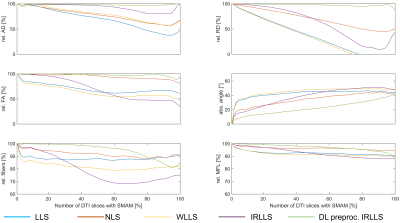
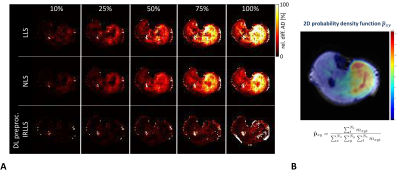
A comparison of a simple signal intensity adaption and the generator approach is given in Fig. 3. FA values are differing between both approaches and the generated SMAM of the model-based procedure looks more realistic. A Sørensen-Dice³¹ coefﬁcient of 87.7±7.6 % (3-fold cross-validation) was achieved for SMAM mask generation. The influence of derived parameters on the amount of SMAM-affected DTI is given in Fig. 4. It is visible that previous detection and segmentation of SMAMs lead to more stable results (up to an amount of 80% SMAM-affected DTI). Fig. 5A shows the AD maps calculated by LLS, NLS and DL preproc. IRLLS. Clear differences are visible in the region of m. soleus and m. gastrocnemius medialis for all three approaches. The 2D probabilistic density map for the SMAM locations of this subject is given in Fig. 5B reflecting the enhanced activity rate in these muscular regions.

Conclusion

The presented concept generates realistic SMAM-affected DTI data sets from undistorted DTI. It was shown that model-based preprocessing and exclusion of SMAMs in DTI data sets in conjunction with a robust diffusion tensor estimation approach leads to more stable results even at high activity rates.
In further studies, this concept should be able to estimate the influence of SMAMs in DTI data sets and potentially enables the interpretation of the differences in derived DTI parameters between healthy subjects and patients suffering from neuromuscular disease.

Acknowledgements

This work was supported and funded by the German Research Foundation (DFG) under Grants SCHI 498/11‐1 and YA 28/16‐1.

References

[1]: Chang LC, Jones DK, Pierpaoli C. RESTORE: Robust Estimation of Tensors by Outlier Rejection. Magnetic Resonance in Medicine 53:1088-1095. 2005.

[2]: Chang LC, Walker L, Pierpaoli C. Informed RESTORE: A Method for Robust Estimation of Diffusion Tensor from Low Redundancy Datasets in the Presence of Physiological Noise Artifacts. Magnetic Resonance in Medicine 68:1654-1663. 2012.

[3]: Collier Q, Veraart J, Jeurissen B, den Dekker AJ, Sijbers J. Iterative Reweigted Linear Least Squares for Accurate, Fast, and Robust Estimation of Diffusion Magnetic Resonance Paramters. Magnetic Resonance in Medicine 73:2174-2184. 2015.

[4]: Giraudo C, Motyka S, Weber M, Resinger C, Feiweier T, Traxler H, Trattnig S, Bogner W. Weighted Mean of Signal Intensity for Unbiased Fiber Tracking of Skeletal Muscles. Investigative Radiology 52(8). 2017.

[5]: Karampinos D, Banerjee S, King KF, Link TM, Majumdar S. Considerations in high resolution skeletal muscle DTI using single-shot EPI with stimulated echo preparation and SENSE. NMR Biomed 25(5):766-778. 2012.

[6]: Steidle G, Schick F. Addressing spontaneous signal voids in repetitive single-shot DWI of musculature: spatial and temporal patterns in the calves of healthy volunteers and consideration of unintended muscle activities as underlying mechanism. NMR Biomed 28(7):801-10, 2015.

[7]: Schwartz M, Steidle G, Martirosian P, Ramos-Murguialday A, Preißl H, Stemmer A, Yang B, Schick F. Spontaneous mechanical and electrical activities of human calf musculature at rest assessed by repetitive single-shot diffusion-weighted MRI and simultaneous surface electromyography. Magnetic Resonance in Medicine 79:2784-2794. 2018.

[8]: Whittaker R, Porcari P, Braz L, Williams TL, Schofield IS, Blamire A. Functional magnetic resonance imaging of human motor unit fasciculation in amyotrophic lateral sclerosis. Annals of Neurology 85(3). 2019.

[9]: Schwartz M, Martirosian P, Steidle G, Küstner T, Yang B, Stemmer A, Feiweier T, Schöls L, Synofzik M, Schick F. Measuring Spontaneous Muscular Activities in Neuromuscular Disease: Preliminary Results. Proc. ISMRM 2020.

[10]: Fitzurka MA, Tam DC. A joint interspike interval difference stochastic spike train analysis: detecting local trends in the temporal ﬁring patterns of single neurons. Biological Cybernetics 80:309–326. 1999.

[11]: Kleine BU, Stegeman DF, Schelhaas HJ, Zwarts MJ. Firing pattern of fasciculations in ALS: evidence for axonal and neuronal origin. Neurology 70:353–359. 2008.

[12]: Bashford J, Wickham A, Iniesta R, Drakakis E, Boutelle M, Mills K, Shaw CE. Preprocessing surface EMG data removes voluntary muscle activity and enhances SPiQE fasciculation analysis. Clinical Neurophysiology 131:265–273. 2020.

[13]: Goodfellow I, Pouget-Abadie J, Mirza M, Xu B, Warde-Farley D, Ozair S, Courville A, Bengio Y. Generative Adversarial Networks. NIPS. 2014.

[14]: Mirza M, Osindero S. Conditional Generative Adversarial Nets. arXiv:1411.1784. 2014.

[15]: Gilliam C, Küstner T, Blu T. 3D Motion Flow Estimation using Local All-Pass Filters. Proc. IEEE Int. Symp. Biomed. Imag. (ISBI). 2016.

[16]: Küstner T, Neumann V, Schwartz M, Würslin C, Martirosian P, Gatidis S, Schwenzer NF, Schick F, Yang B, Schmidt H. An MR Motion Correction toolbox for registration and evaluation. ISMRM 2016.

[17]: Ronneberger O, Fischer P, Brox T. U-net: Convolutional Networks for Biomedical Image Segmentation. Medical Image Computing and Computer-Assisted Intervention (MICCAI). Springer, LCNS, Vol.9351:234-241. 2015.

[18]: Wang Z, Bovik AC, Sheikh HR, Simoncelli EP. Image quality assessment: from error visibility to structural similarity. IEEE Transactions on Image Processing 13(4):600–612. 2004.

[19]: Maurer C, Rensheng Q, Raghavan V. A Linear Time Algorithm for Computing Exact Euclidean Distance Transforms of Binary Images in Arbitrary Dimensions. IEEE Transactions on Pattern Analysis and Machine Intelligence 25(2):265-270. 2003.

[20]: Koay CG. Least squares approaches to diffusion tensor estimation. In: Jones D, editor. Diffusion MRI. New York: Oxford University Press:281–343. 2011.

[21]: Koay CG, Chang LC, Carew JD, Pierpaoli C, Basser PJ. A unifying theoretical and algorithmic framework for least squares methods of estimation in diffusion tensor imaging. Journal of Magnetic Resonance 182:115–125. 2006.

[22]: Basser PJ, Mattiello J, Le Bihan D. Estimation of the effective self-diffusion tensor from the NMR spin echo. Journal of Magnetic Resonance 103: 247–254. 1994.

[23]: Salvador R, Pena A, Menon DK, Carpenter TA, Pickard JD, Bullmore ET. Formal characterization and extension of the linearized diffusion tensor model. Hum Brain Mapp 24:144–155. 2005.

[24]: Veraart J, Sijbers J, Leemans A, Jeurissen B. Weighted linear least squares estimation of diffusion MRI parameters: strengths, limitations, and pitfalls. NeuroImage 81:335–346. 2013.

[25]: Schwartz M, Küstner T, Martirosian P, Machann J, Steidle G, Yang B, Schick F. Robust Quantification of Spontaneous Muscular Activities by Simultaneous Interpretation of sEMG Data. ESMRMB 2019.

[26]: Schwartz M, Martirosian P, Steidle G, Erb M, Stemmer A, Yang B, Schick F. Volumetric assessment of spontaneous mechanical activities by simultaneous multi-slice MRI techniques with correlation to muscle fiber orientation. NMR Biomed 31(11). 2018.

[27]: Basser PJ, Pajevic S, Pierpaoli C, Duda J, Aldroubi A. In vivo ﬁber tractography using DT-MRI data. Magnetic Resonance in Medicine 44:625–632. 2000.

[28]: Yeh FC, Verstynen TD, Wang Y, Fernandez‐Miranda JC, Tseng WY. Deterministic diffusion fiber tracking improved by quantitative anisotropy. PLoS ONE 8(11):e80713. 2013.

[29]: Lansdown DA, Ding Z, Wadington M, Hornberger JL, Damon BM. Quantitative diffusion tensor MRI‐based fiber tracking of human skeletal muscle. J Appl Physiol 103(2):673‐681. 2007.

[30]: Damon BM, Froeling M, Buck AK, Oudeman J, Ding Z, Nederveen AJ, Bush EC, Strijkers GJ. Skeletal muscle diffusion tensor‐MRI fiber tracking: rationale, data acquisition and analysis methods, applications and future directions. NMR Biomed 30(3):e3563. https://doi.org/10.1002/nbm.3563. 2017.

[31]: Lee R. Dice. Measures of the amount of ecologic association between species. Ecology 26:297–302, 1945.

Figures

Figure 1: A: Concept for SMAM generation and insertion into an undistorted DTI data set. SMAM activity rate and location can be estimated from DWI and transferred on the DTI data sets. B: Training of the mask generator with a skeletonized label mask m and Gaussian noise. C: Training of the generator for SMAM insertion with a separated background and foreground loss to preserve background signal intensity.

Figure 2: MR sequence parameters of the DWI and DTI data sets.

Figure 3: A: Original DTI with a new SMAM mask for insertion. Simple reduction of the signal intensity by multiplication leads to unrealistic images in comparison to the model-based output. B: Differences in FA between model-based and simple SMAM generation are visible.

Figure 4: Relative change of median AD, RD, FA, number of fibers, MFL and absolute angle deviation in relation to the relative amount of SMAM-affected DTI slices. Preprocessing by SMAM detection and segmentation leads to a more robust estimation of DTI parameters in most cases up to an amount of 80% of SMAM-affected DTI.

Figure 5: A: Axial diffusivity maps for LLS, NLS and the model-based preprocessing approach and for different amounts of SMAM-affected DTI (from 10% to 100%). B: 2D probability density function for the location of the SMAM occurrences in the right lower leg. The high activity rate is reflected by large deviations in the AD maps in the region of m. soleus and m. gastrocnemius medialis.

Proc. Intl. Soc. Mag. Reson. Med. 29 (2021)

0584