Introduction

Motion poses a major challenge in clinical brain MRI. Nearly 30% of inpatient scans suffer from motion artifacts¹. Numerous efforts have been made to address brain motion^2-4, but no one solution has been generalizable enough to tackle all motion types⁵. Quantitative multiparametric mapping, which measures biomarkers offering complementary tissue information for disease evaluation^6-7, is especially prone to motion artifacts due to prolonged scan times. Here, we introduce a stand-alone motion-resolved approach to quantitative multiparametric mapping using Multitasking, which is generalizable to translation, rotation, discrete motion, and periodic motion without explicit need for motion correction/compensation.

Methods

Image model:
Multitasking conceptualizes overlapping image dynamics as different time dimensions⁸, leading to an underlying image $$$x\left(\mathbf{r},t_{1},t_{2},\ldots,t_{N},s\right)$$$ with spatial index $$$\mathbf{r}$$$, motion state index $$$s$$$, and $$$N$$$ time index $$$t_{i}$$$ related to quantifiable parameters of interest (e.g., T1/T2/T1$$$\rho$$$/T2*/ADC). This image can be rearranged into an ($$$N$$$+2)-way low-rank⁹ tensor $$$\mathcal{X}$$$, which can be decomposed as¹⁰:
$$\mathcal{X}=\mathcal{V}\times_{1}\mathbf{U}_{r},$$
$$\mathcal{V}=\mathcal{C}\times_{2}\mathbf{U}_{t_{1}}\times_{3}\mathbf{U}_{t_{2}}\times_{4}\ldots\times_{N+1}\mathbf{U}_{t_{N}}\times_{N+2}\mathbf{U}_{s},$$
where $$$\mathcal{C}$$$ denotes the core tensor, each $$$\mathbf{U}$$$ is the factor matrix for the corresponding dimension, and $$$\times_{i}$$$ denotes $$$i$$$-mode tensor product¹¹.

Image reconstruction:
Fig. 1 shows the image reconstruction pipeline.

First, an image with a single time dimension $$$t$$$ representing elapsed time, denoted as $$$\mathbf{X_{\mathrm{rt}}}$$$, is reconstructed using low-rank matrix strategy^9,12.

Second, the last recovery time of each shot is extracted from $$$\mathbf{X_{\mathrm{rt}}}$$$, denoted as $$$\mathbf{X_{s}}$$$. Feature matrix $$$\mathbf{F}=\left(\mathbf{f}_{1},\mathbf{f}_{2},\ldots,\mathbf{f}_{N_{s}}\right)$$$ is extracted from $$$\mathbf{X_{s}}$$$ via PCA ($$$N_{s}$$$ denotes the number of recovery periods). To identify different motion states, k-means clustering is performed on $$$\mathbf{F}$$$. To select the number of motion states/clusters $$$K$$$, the algorithm is performed for $$$K$$$=1,2,…,20. Euclidean distance is calculated for each $$$K$$$:
$$d_{K}=\sum_{k=1}^{K}\sum_{\mathrm{f}_{s}\in{C_{k}}}\left\|\mathbf{f}_{s}-\mathbf{c}_{k}\right\|^{2},s\in\left\{1,2,\ldots,N_{s}\right\}$$
where $$$\mathbf{c}_{k}$$$ is the centroid of the $$$k$$$th cluster $$$C_{k}$$$. We choose $$$K$$$ from the elbow of $$$(K, d_{K})$$$ plot.

Third, the multidimensional factor $$$\hat{\mathcal{V}}$$$ is recovered from Bloch-constrained small-scale low-rank tensor completion of subspace training data $$$\mathbf{D_{\mathrm{tr}}}$$$^8,12-13.

Fourth, to reduce the effect of outlier motion, a diagonal weighting matrix $$$\mathbf{W}$$$ is calculated from the residual comparing $$$\mathbf{D_{\mathrm{tr}}}$$$ to $$$\hat{\mathbf{V_{\mathrm{rt}}}}$$$ (i.e., $$$\hat{\mathcal{V}}$$$ mapped back to single-time domain):
$$\mathbf{R}=\mathbf{D}_{\mathrm{tr}}-\mathbf{D}_{\mathrm{tr}}\widehat{\mathbf{V}}_{\mathrm{rt}}^{\dagger}\widehat{\mathbf{V}}_{\mathrm{rt}},$$
$$W_{jj}=\left(\sum_{i}\left|R_{ij}\right|^{2}\right)^{-1/2}.$$

Fifth, $$$\mathbf{U}_{r}$$$ is estimated by solving:
$$\mathbf{U}_{r}=\arg\min_{\mathbf{U}_{r}}\left\|\mathbf{W}\left[\mathbf{d}_{\mathrm{img}}-E\left(\hat{\mathcal{V}}\times_{1}\mathbf{U}_{r}\right)\right]\right\|^{2}+R_{s}\left(\mathbf{U}_{r}\right),$$
where $$$\mathbf{d}_{\mathrm{img}}$$$ represents the vectorized imaging data^8,12-13, $$$E$$$ combines multichannel encoding and sampling, and $$$R_{s}(\cdot)$$$ performs spatial regularization.

Lastly, multiparametric fitting^8,12-13 is performed on $$$\mathcal{X}$$$ selecting the most-populous motion state.

Motion simulation:
3D whole-brain T1/T2/T1$$$\rho$$$ maps¹³ were used to generate a numerical motion phantom which was used to simulate 15min Multitasking scan¹³. Two motion schemes were investigated including 8 scenarios:

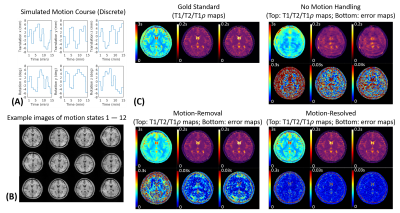
Discrete motion: 6 scenarios were simulated with 2,3,4,5,6,12 discrete motion states. For each scenario, three translations and three rotations along and around xyz axis were selected from [-8mm,8mm] and [-8°,8°] following Gaussian distribution for each motion state.

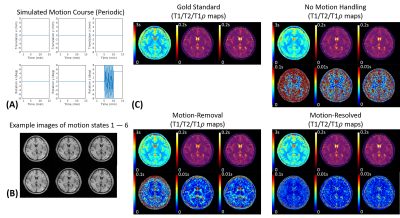
Periodic motion: 2 scenarios were simulated where z-rotation from [-8°,8°] (simulating head shaking) were periodically added during the middle 5min of the simulated scan. For one scenario, the head returned to the original 0° position after motion; for the other, the head rotated to a different 5° position after motion.

For each scenario, we went through the estimation of $$$K$$$ and motion state clustering.

In vivo experiments:
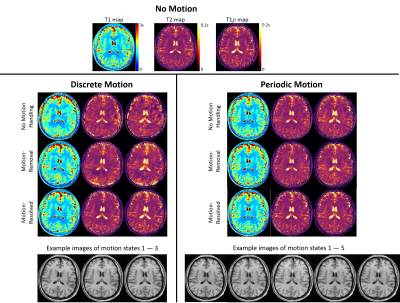
Data were collected on $$$n$$$=2 healthy subjects on Siemens Biograph mMR scanner. A Multitasking T1/T2/T1$$$\rho$$$ mapping sequence¹³ was implemented with FOV=240x240x140mm³, resolution=1.0x1.0x3.5mm³, scan time=7min. For each subject, one motion-free scan was performed followed by two motion scans: one containing discrete motion for at least 2 movements, the other containing periodic motion for at least 2min. Each subject was given instructions of the motion type and the minimum amount of motion to be performed.

Evaluations:
Three reconstructions were compared: i) no motion-handling, where all k-space data were used for reconstruction assuming a single motion state ($$$K$$$=1); ii) motion-removal, where k-space data outside of the most-populous state were discarded; iii) motion-resolved, as described above. For the simulations, RMSE of reconstructed T1/T2/T1$$$\rho$$$ maps compared to phantom ground truth were calculated for evaluation.

Results

Fig.2A shows the simulated motion pattern for the discrete motion scenario with 12 states. Our algorithm correctly determined $$$K$$$=12, and all those states were successfully identified (Fig.2B). The motion-resolved solution produced substantially reduced absolute difference errors compared to no motion-handling and motion-removal (Fig.2C).

Fig.3A shows the motion pattern for the periodic motion scenario with 5 ending position. $$$K$$$=6 motion states were binned by our algorithm (Fig.3B). Again, the motion-resolved solution produced substantially reduced absolute difference errors against the gold standards (Fig.3C).

Fig.4 shows the RMSE of the reconstructed T1/T2/T1$$$\rho$$$ maps against the gold standards for all 8 simulated scenarios. The proposed solution substantially reduced RMSE for T1/T2/T1$$$\rho$$$.

Fig.5 shows example in vivo results for discrete and periodic motion. Three motion states were identified for discrete motion, and 5 motion states were identified for periodic motion. For both experiments, the motion-resolved solution produced T1/T2/T1$$$\rho$$$ maps with the best image quality with less ghosting/blurring artifacts and sharper tissue structures.

Discussion and Conclusion

We introduced a motion-resolved solution for quantitative brain multiparametric mapping, which outperformed no motion-handling and motion-removal. Feasibility was demonstrated for T1/T2/T1$$$\rho$$$ mapping, with extension to other quantifiable tissue parameters straightforward using Multitasking. The proposed solution works as a stand-alone approach which is generalizable to translation, rotation, discrete motion, and periodic motion, with no explicit need for motion correction/compensation.

Acknowledgements

This work was supported by NIH 1R01EB028146.