Introduction

Diffusion time-dependence can be used to infer microstructural information from the diffusion-weighted signal.^1,2 Measurement strategies that independently probe restricted diffusion and exchange yield estimates of cell size and permeability. ^3–6 The restriction-exchange framework by Nilsson et al.⁷ uses free gradient waveforms described by two experiment parameters which capture restriction and exchange weighting. The framework is based on a second-order cumulant expansion which fails to capture signal decay at high b-values, and it relies on assumptions that only hold for short diffusion times and low frequencies in the diffusion spectrum.
Here, we propose a two-compartment restriction-exchange model that accommodates arbitrary gradient waveforms and is valid at all b-values, encoding times and frequencies in the diffusion spectrum. We validate the theory by using Monte-Carlo simulations of restricted diffusion and water exchange on a synthetic substrate.

Theory

We begin with the Kärger equations describing signal evolution between two spin ensembles (S1 and S2)
$$ \frac{\partial}{\partial t} \bigg ( \begin{matrix} S_1 \\ S_2 \end{matrix} \bigg) = [K - Dq(t)^2] \bigg ( \begin{matrix} S_1 \\ S_2 \end{matrix} \bigg) \hspace{24pt} (1)$$
where $$$K$$$ and $$$D$$$ are matrices of exchange rates and intrinsic diffusivities,

$$K = \begin{bmatrix}-k_{12} & k_{21} \\k_{12} & -k_{21} \\\end{bmatrix} \hspace{12pt}; \hspace{12pt} D = \begin{bmatrix}D_1 & 0 \\0& D_2\\\end{bmatrix}$$

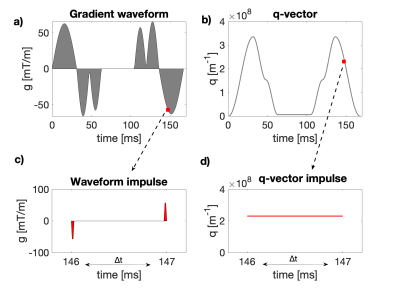
and $$$q(t)$$$ is the dephasing vector as a function of time. When q is piecewise constant in time (e.g. SDE or DDE with short gradient pulses), Eq.1 has closed-form solutions. We derive a solution for any $$$q(t)$$$ by treating a gradient waveform as comprising a pair of impulses in every time-step $$$\Delta t$$$ (Fig.1).⁹ This results in a constant q-vector in every $$$\Delta t$$$, allowing us to solve Eq.1 and arrive at the generalized solution

$$ S(q, \Delta t, N) = \boldsymbol{1}\cdot \prod_{i=1}^{N} \exp([K - Dq_i^2]\Delta t )\cdot F \hspace{24pt} (2)$$

where $$$ \boldsymbol{1} = [1 \hspace{6pt} 1]$$$, $$$F = [f_1 \hspace{6pt} f_2]'$$$ is a vector of signal fractions and $$$N = T/\Delta t$$$ for a total diffusion encoding time $$$T$$$. This places no restriction on $$$q(t)$$$ and is thus applicable for arbitrary gradient waveforms. Eq.1 can be shown to adhere to previous theory ⁸ by taking its cumulant expansion to arrive at

$$S/S_0 \approx \exp(-\bar{D}b + \frac{1}{2}\text{Var}(D)\cdot (1 - k\cdot \Gamma)b^2) \hspace{24pt} (3)$$
where $$$\bar{D}$$$ and Var(D) are the mean and variance of diffusivities, and
$$\Gamma = \frac{Q_4}{3b^2}$$
where
$$ Q_4:= \sum_{i=1}^{N} (q_i^4 \Delta t^2)\Delta t + \sum_{j=1}^{N-1} \bigg( 6j\cdot \sum_{i=1}^{N-j}q_i^2q_{i+j}^2 \Delta t ^2 \bigg)\Delta t$$

Eqn.2 describes exchange in a two-component free diffusion setting, which does not address our goal of developing a two-compartment model. Following previous work ¹⁰, we account for restriction by introducing geometry-dependent apparent diffusivities given by
$$D(\cdot) = \frac{1}{2\pi b}\int_{-\infty}^{\infty} D(\omega)|Q(\omega)|^2d\omega \hspace{24pt} (4)$$
where $$$D(\omega)$$$ is the diffusion spectrum and $$$|Q(\omega)|^2$$$ is the encoding power spectrum. Here, $$$D(\omega)$$$ refers to the full spectrum, in contrast to its Taylor expansion used in previous work ¹⁰. Our final restriction-exchange model is then defined by
$$ S(q, \Delta t, N) = \boldsymbol{1}\cdot \prod_{i=1}^{N} \exp([K - \hat{D} q_i^2]\Delta t )\cdot F \hspace{24pt} (5)$$

where
$$\hat{D} = \begin{bmatrix}D(\cdot) & 0 \\0& D_2\\ \end{bmatrix}$$

Methods

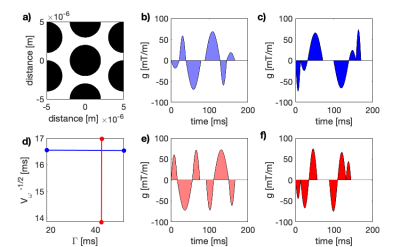
Random walkers were simulated on a continuous 2D synthetic substrate consisting of regularly distributed circular permeable cells (Fig.2a). Exchange was implemented as described by Szafer ¹¹. Simulation parameters were:

$$N_{particles} = 10^5, \Delta t = 10 \hspace{4pt} \mu\text{s}, f_1 = 0.7, D_1 = D_2 = 1.2 \hspace{4pt} \mu\text{m}^2/\text{ms}$$
$$k = [0, 2, 4, 6, 8, 10] \hspace{4pt} \text{ s}^{-1} \text{ at } d = 10 \hspace{4pt} \mu\text{m}, d = [4, 8, 12, 16, 20] \hspace{4pt}\mu\text{m at } k = 10 \text{ s}^{-1}, \hspace{4pt} T = 300 \text{ ms}.$$
Signals were generated using a protocol with different exchange- and restriction weightings as previously proposed by us (Figure 2b). The signals featured maximum b-values between 5 and 30 ms/µm$$$^ 2$$$ arrived at in 10 steps. Eq.5 was fitted by nonlinear-least-squared fitting to the signals to evaluate accuracy of estimates. Noise was added at $$$SNR = 100$$$ to investigate precision.

Results

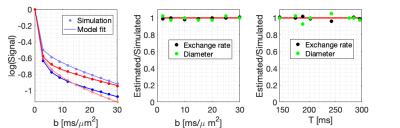
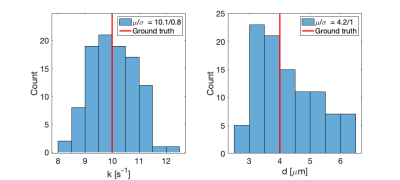
Figure 3 shows the response of the developed theory to varying scenarios of restriction and exchange and demonstrates a good fit to simulated data. Estimates of exchange rate and compartment diameter are in harmony with ground truth. The figure also shows that our model correctly detects the fixed value of one parameter while the other is being varied. This is evidence of the ability to independently account for restriction and exchange. Model validity at high b-values and long encoding times is confirmed in Fig.4 which shows that our model fits the data well, at least up to b=30 ms/µm$$$^2$$$. Size and exchange estimates remain stable over all simulated b-values and encoding times. Precision in parameter estimates is depicted in Fig.5. The distributions are well-centered around the ground truth, with some slight skewing evident in the size estimates.

Discussion

We developed and validated a generalised exchange-restriction two-compartment model that is applicable to acquisitions with arbitrary gradient waveforms and any range of b-values and diffusion encoding times. The proposed representation can be used to obtain reliable parameter estimates in conditions where the cumulant expansion would fail. A possible shortcoming of the approach is the relatively large variance in size estimates. Future work will address this using protocol optimisation. ¹²

Acknowledgements

No acknowledgement found.