0468
Joint Estimation and Correction of Motion and Geometric Distortion in Segmented 3D Arterial Spin Labeling1Fraunhofer MEVIS, Bremen, Germany, 2University of Bremen, Bremen, Germany
Synopsis
Assessement of CBF using Arterial Spin Labeling (ASL) can yield valuable functional information regarding different neuropathological diseases like tumors and stroke without exogenous contrast agents. However, being a subtractive technique, ASL shows high sensitivity to motion artifacts. ASL in combination with a 3D GRASE PROPELLER (3DGP) readout allows self-navigated retrospective motion correction but motion estimates using the standard reconstruction are inaccurate due to geometric distortion. In this work, a novel 3DGP reconstruction algorithm is therefore demonstrated which jointly estimates the distortion field as well as motion parameters without the need for additional reference scans.
Introduction
Assessment of cerebral blood flow (CBF) can give valuable additional information regarding tumors [1], Alzheimer’s disease [2] and stroke [3][4]. Arterial spin labeling (ASL) magnetic resonance imaging (MRI) allows non-invasive measurements and quantification of CBF by magnetically inverting the inflowing blood, utilizing it as endogenous tracer. Unfortunately, ASL shows high sensitivity to motion due to its subtractive nature, leading to corrupted images. 3D GRASE PROPELLER (3DGP) ASL enables self-navigated retrospective motion correction [5][6]. However, 3DGP ASL never found wide application; the major reason being that the accuracy of motion detection in 3DGP is currently limited due to the neglection of geometric distortion in the motion estimation algorithm. We therefore hypothesize that the full potential of pseudo-continuous ASL (pCASL) with 3DGP readout has not yet been exploited and that current limitations can be overcome by a novel approach called 3DGP-JET (3DGP with Joint Estimation of Motion and Geometric Distortion).Theory
The signal of the i-th complex 3DGP navigator after inverse Fourier transform along the z-direction can be written as$$ s_i(\vec{k},z) = \sum_{x,y} \rho(\vec{r}, z) \text{exp}[-i\frac{2 \pi}{N_\text{x}}k_\text{x} x]\text{exp}[-i\frac{2 \pi}{N_\text{y}}k_\text{y} y] (1)$$
with $$$\vec{r}=(x,y)^T$$$ the position in image space, $$$N_\text{x},N_\text{y}$$$ the number of pixels of the low-resolution navigator and $$$k_\text{x},k_\text{y}$$$ the position in k-space. Two-dimensional rigid-body motion is integrated into Eq. 1 by exploiting the shift and rotational theorem of the Fourier transform. In addition, local displacements $$$\vec{D}_i=[\frac{2\pi}{N_\text{x}}\text{sin}(\alpha_i), -\frac{2\pi}{N_\text{y}}\text{cos}(\alpha_i)] \cdot d(\vec{r},z)$$$ with the angle $$$\alpha_i$$$ of the phase-encoded direction are integrated as follows:
$$s_i(\vec{k},z)=\sum_{x,y} \rho(\vec{r}, z) \text{exp}[-\text{i}\frac{2 \pi}{N_\text{x}} (R_{i,+} \cdot \vec{k})_\text{x} (x + (R_{i,-} \cdot \vec{D}_i)_\text{x} + t_{i,\text{x}})] \text{exp}[-\text{i}\frac{2 \pi}{N_\text{y}} (R_{i,+} \cdot \vec{k})_\text{y} (y + (R_{i,-} \cdot \vec{D}_i)_\text{y} + t_{i,\text{y}})] \\ \Rightarrow s_i(\vec{k},z) = A_i[\rho](\vec{k},z)(2)$$ Here, $$$R_{i,+}$$$ and $$$R_{i,-}$$$ depict the rotational matrices applying rotations $$$\pm \phi_i$$$ and $$$t_{i,\text{x}}, t_{i,\text{y}}$$$ are translational shifts.
A solution to Eq. 2 is found by minimizing the functional $$e(\rho(\vec{r}, z), d(\vec{r}, z), \alpha_i, t_{i,\text{x}}, t_{i,\text{y}}) =\sum_i \sum_z \sum_\vec{k} ( s_i(\vec{k}, z) - A_i[\rho](\vec{k},z) )^2 + \lambda TV_3(d(\vec{r},z)) (3)$$ with respect to $$$\rho(\vec{r}, z)$$$, $$$d(\vec{r}, z)$$$ and $$$\phi_i, t_{i,\text{x}}, t_{i,\text{y}}$$$. The regularization term $$$\lambda TV_3(d(\vec{r}, z))$$$ enforces smooth field maps by penatilizing the total variation.
Methods
Scans are performed on a 3T Siemens Skyra Magnetom. Three healthy volunteers (2 male, 1 female, mean age: (31 ± 7) years) were scanned using a 3DGP and segmented 3D GRASE readout without intentional motion. Scans were repeated and moderate in-plane head rotation was performed approximately every 20 seconds during the labeling period. Background suppression and 3DGP acquisition schemes are shown in Fig. 1.3DGP scans are reconstructed using the proposed 3DGP-JET (cf. Fig. 2) and standard 3DGP-STD reconstruction[5][6]. For 3D GRASE data, a state-of-the-art reconstruction with retrospective three-dimensional rigid-body motion correction was implemented using the Insight Toolkit [7].
For 3DGP, twenty label/control bricks of size 96x32x8 were acquired in 2:40 minutes, resulting in an image resolution of (3.1x3.1x4) mm³. The same parameters were used to acquire three 3D GRASE segments with five averages yielding a total acquisition time of 2:00 minutes. A label duration/post-labeling delay of 1.8s/1.8s was applied. For 3DGP, TR/TE=4000ms/24ms and echo spacing=0.53ms, for 3D GRASE, TR/TE=4000ms/24.7ms and echo spacing=0.55ms.
Results
Reconstructed perfusion-weighted images are shown in Fig. 3. An example for JET as well as quantitative motion parameters are given in Fig. 4 and 5.Discussion
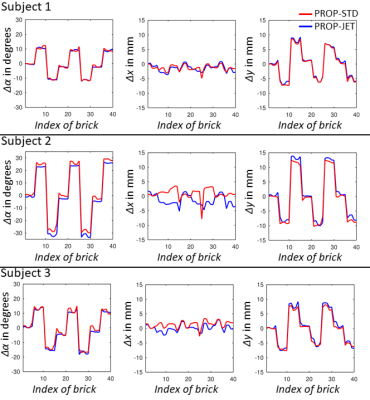
Scans without intentional motion3DGP perfusion-weighted images agree well with 3D GRASE data and no severe increase in blurring due to the higher point spread function of 3DGP is visible (cf. Fig. 3). Comparing rotational standard deviations in Fig. 4b, 3DGP-STD shows higher fluctuation across all subjects than 3DGP-JET, potentially decreasing the accuracy of detected motion or decreasing image quality (cf. increased blurring in zoomed area). Calculated field maps (cf. Fig. 4a) are reasonably, showing slow variation in central brain regions while high-frequent changes occur near air-tissue interfaces. Although visible correction of distorted areas is shown (cf. Fig. 4 arrows), the current approach was not able to correct for all distorted areas in all subjects. This limitation most likely arises from a loss in accuracy of field maps due to interpolation operations which is further investigated.
Scans with intentional motion
3DGP-JET shows high quality perfusion-weighted images across all subjects which agree well with images without intentional motion (cf. Fig. 3). Motion corrected 3D GRASE also shows reduction of artifacts. However, structural background noise is introduced due to ghosting which can not be corrected and which will be more severe for high-frequent motion. Comparing 3DGP-STD and 3DGP-JET, estimated motion trajectories correlate well (cf. Fig. 5) while 3DGP-JET shows less artifacts due to the filtration of bricks with non-cancelled fat signal. While this shows to be an effective solution for low-frequent motion patterns, the application to high-frequent patterns is limited. Sophisticated background and fat suppression is therefore of high importance for motion correction techniques and the effects on 3DGP-JET and 3DGP-STD will be addressed in future studies.
Conclusion
A novel reconstruction algorithm for 3DGP ASL has been succesfully validated with and without intentional subject motion. In addition to accurate motion estimates, B0-inhomogeneity is estimated and corrected without additional scans. Future studies will investigate the algorithms effectiveness in different scenarios of background suppression and with intentional high-frequent motion patterns.Acknowledgements
Funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – 446287025.References
[1] Fujima et al., "Arterial spin labeling to determine tumor viability in head and neck cancer before and after treatment", Journal of Magnetic Resonance Imaging 40, 2013.
[2] Wolk, Detre, „Arterial spin labeling MRI: MRI: An Emerging Biomarker for Alzheimer's Disease and Other Neurodegenerative Conditions“, Current Opinion in Neurology 25, 2012.
[3] Thamm et al., „Diagnostic and prognostic benefit of arterial spin labeling in subacute stroke“, Brain and Behavior 9, 2019.
[4] Zaharchuk, „Arterial Spin–Labeled Perfusion Imaging in Acute Ischemic Stroke“, Stroke 45, 2014.
[5] J. G. Pipe, „Motion correction with PROPELLER MRI: Application to head motion and free-breathing cardiac imaging“, Magnetic Resonance in Medicine 42, 1999.
[6] Tan et al., „3D GRASE PROPELLER: Improved image acquisition technique for arterial spin labeling perfusion imaging“, Magnetic Resonance in Medicine 66, 2011.
[7] McCormick et al., „ITK: enabling reproducible research and open science“, Frontiers in Neuroinformatics 8, 2014.
Figures
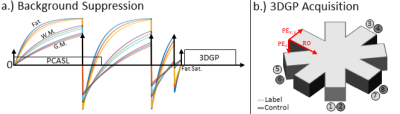
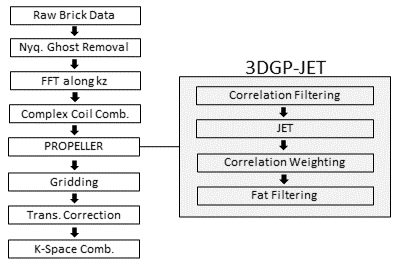
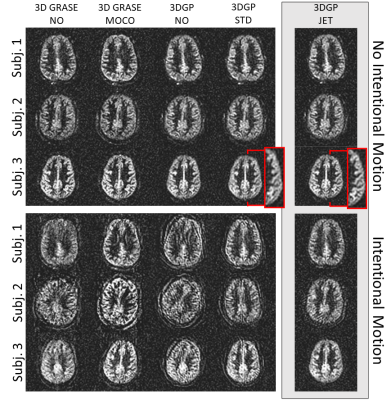
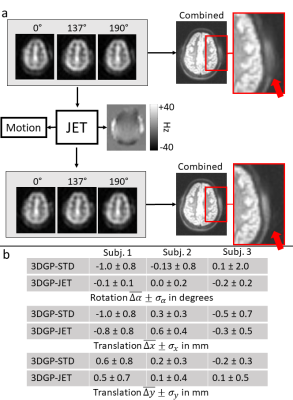
Figure 4: a.) Procedure of 3DGP-JET. All bricks (three out of twenty control bricks from the third subject shown here) are used to estimate the underlying distortion field and individual motion parameters (Eq. 3). The distoriton field is then used to compensate distortion in individual bricks by unwarping with interpolated inverse field maps. Arrows indicate areas with large off-resonances and visible distortion in uncorrected 3DGP images; and b.) Mean and standard deviation of calculated motion parameters for the datasets without intentional motion using 3DGP-JET and 3DGP-STD.