Introduction

3D multi-shot EPI, as the most popular 3D fMRI method, generally fails to fully provide the SNR benefit compared to 2D imaging^1,2. This is partly because of the increased vulnerability to respiration induced spatially varying B0 fluctuations, which can manifest themselves as inter-shot phase variations. As the field moves towards higher isotropic resolutions for more spatially specific fMRI, which can only be achieved with 3D encoding, addressing this issue is becoming increasingly relevant, particularly at ultra-high fields like 7T which have higher SNR but more severe off-resonance effects. Here, we explored the impact of different 3D segmented CAIPI EPI sampling trajectories, which show varying vulnerabilities to B0 fluctuations, and an improved reconstruction method based on annihilating filter Hankel structured low-rank matrix completion^3,4,5,6, to improve the temporal stability of 3D multi-shot EPI at 7T.

Methods

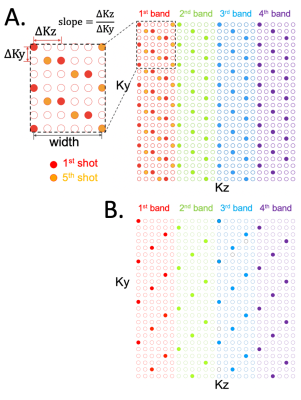
We describe the 3D EPI trajectory as a segmented, band-limited CAIPI sampling scheme^7,8, denoted as “seg-CAIPI(width, slope)” (Fig.1). The 3D k-space is divided into "bands" along k_z and an interleaved sampling approach is used where sampling loops through bands first. Each shot samples a band using a CAIPI k_z-blipped readout specified by the parameters “width” and “slope”. The offset between two consecutive shots in the same band is chosen to approximate a golden ratio offset, and there is a ∆=1 CAIPI shift in k_y across bands in acquisitions with in-plane acceleration(Fig.1B). Note that a "standard", CAIPI k_y-blipped 3D multi-shot EPI trajectory is achieved by setting width=1, slope=0.
As respiration effects are temporally coherent on the shot-to-shot timescale, we bin a small number of consecutive shots together as a pseudo shot(acquisition window~0.5s), assuming the intra-bin inconsistencies are negligible. The above sampling scheme makes each pseudo shot have a much more uniform k-space coverage than the “standard” trajectory. Unlike conventional reconstructions which combine all the shots together for a single volume irrespective of the inter-shot phase inconsistencies, our method aims to reconstruct an individual image for each pseudo-shot, and then pseudo-shot images are sum-of-squares combined to remove the impact of differential phase. The missing k-space data for each pseudo-shot is jointly recovered by a sensitivity encoded, low-rank constrained optimisation solved via ADMM:
$${\underset {X}{\operatorname {arg\,min} }}||E·X-Y||_2^2+\lambda||H·X||_*$$
where X is the unknown composite k-space with an additional pseudo-shot dimension for a single volume, the forward model E performs the sensitivity encoding and sampling, Y is the measured data and λ is the regularisation parameter. The operator H generates the block-Hankel representation of X, and the nuclear norm $$$||H·X||_*$$$enforces its low-rankness⁴. Note the reconstruction is performed independently on every time-point.
Simulation experiments. Physiologically plausible phase variation maps derived from a 2D EPI time series acquired at 7T were used to simulate multi-shot k-space datasets consisting of a single k_y-k_z plane, added with different amount of Gaussian noise to simulate varying thermal noise levels. A dataset with Gaussian noise only was also generated as a reference for the optimal tSNR upper bound.
In-vivo experiments. Two subjects were scanned on a Siemens Magnetom 7T scanner with different protocols to assess tSNR. [1.5 mm isotropic resolution]: matrix size=140*140*96, 96 shots/volume, in-plane acceleration R_PE=3, TE/TR=20/40ms; [1.8 mm isotropic resolution]: matrix size=108*108*96, 96 shots/volume, in-plane acceleration R_PE=2, TE/TR=22/42ms. Multiple datasets with different trajectories were acquired for each subject. The 1.8 mm data was retrospectively under-sampled along the shot dimension for an additional R_3D=2/4/6 (R_net=R_PExR_3D). A third subject was scanned using the 1.8 mm protocol(with R_3D=2 retrospective under-sampling) in a block-design visual checkerboard experiment to assess impact on BOLD activation maps.

Results and Discussions

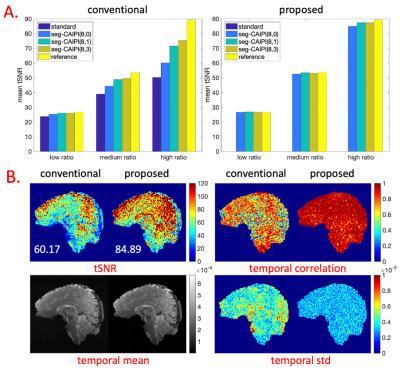
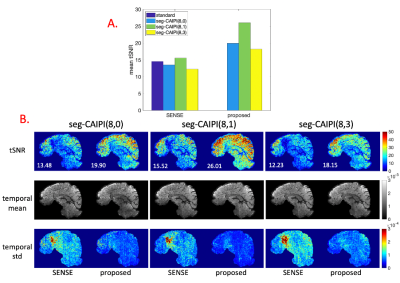
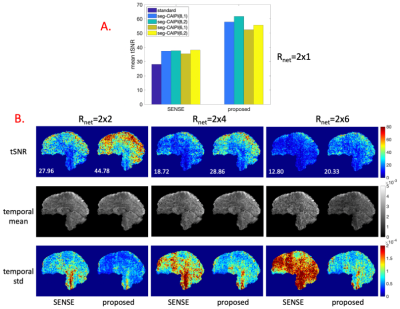
The proposed reconstruction bins 12 shots per pseudo shot for all experiments. Figure 2 shows the results of reconstructing fully sampled simulation data by the conventional and the proposed approaches(λ=3*1E-5). The tSNR decrease caused by phase variations is trajectory dependent in conventional reconstructions, despite identical overall full k-space coverage, and this trajectory dependency gets stronger as physiological to thermal noise ratio increases. The proposed reconstruction eliminates the trajectory dependency by mitigating the tSNR decrease caused by phase variations.
Figures 3 and 4 show the in-vivo results by the conventional shot-combined SENSE⁹ reconstruction and the proposed reconstruction for the 1.5 mm data(λ=1E-4) and 1.8 mm data(λ=3*1E-4). For the conventional reconstruction, the seg-CAIPI trajectories have higher tSNR than the “standard” trajectory for the 1.8mm data, but not for the 1.5mm data, which could be due to either thermal noise dominance in the smaller voxels¹⁰ or differences in k-space coverage. In both cases, however, the proposed reconstruction improves tSNR over conventional reconstructions.
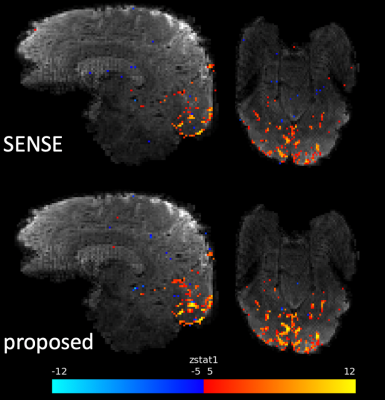
Figure 5 shows the activation maps resulting from the flashing checkerboard experiment. The proposed reconstruction(λ=1E-3) demonstrates higher sensitivity to activation and higher peak z-stats than the shot-combined SENSE reconstruction.

Conclusion

In non-thermal noise dominated regimes, trajectories combining interleaved sampling and CAIPI blips are more favourable for improving the temporal stability in conventional reconstructions, by controlling the temporal variation distribution over the FOV. Additionally, the proposed low-rank constrained reconstruction operates on each volume independently in contrast to spatio-temporal low-rank methods¹¹. It demonstrated a ~50-60% improvement in tSNR compared to conventional reconstruction while retaining full temporal degrees-of-freedom, and is a promising way to improve functional sensitivity for 3D multi-shot EPI fMRI at 7T.

Acknowledgements

No acknowledgement found.