INTRODUCTION

Though functional neuroimaging has revolutionized our understanding of the human brain, additional improvements in imaging methodology for coverage and resolution are continuously pursued for improved neuroscientific studies. Simultaneous multi-slice (SMS)/Multiband (MB) imaging has gained immense interest in functional neuroimaging¹, due to its ability for rapid high-resolution whole-brain coverage². However, high temporal and spatial resolution requirements of fMRI analysis demand higher acceleration rates that are prone to noise amplification with conventional reconstructions. Recently, deep learning (DL) methods have emerged as an alternative for improved accelerated MRI^3-6. However, DL methods typically require fully-sampled data for training, and such data are not available in most highly-accelerated fMRI acquisitions. Furthermore, the effect of DL reconstruction on subsequent fMRI analysis is not clear. In this work, we extend a recently proposed self-supervised DL strategy⁷ to SMS acquisitions, and show the resulting DL reconstruction does not alter the analysis of HCP-style retinotopic mapping acquisition.

METHODS

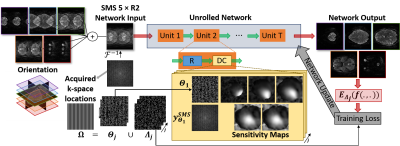
SELF-SUPERVISED DL RECONSTRUCTION FOR SMS FMRI:
We use physics-guided DL reconstruction^3-6, which incorporates the forward encoding model of the acquisition for a regularized reconstruction. The inverse problem for regularized SMS reconstruction is given as
$$\arg \min_{\bf x_1,\cdots,x_S}=\bigg\lVert\mathbf{y}_{SMS}^{\mathbf{\Omega}}-\sum_{i=1}^{S} \mathbf{E}_{i}^{\mathbf{\Omega}}\mathbf{x}_i\bigg\rVert_{2}^{2}+\cal{R}(\mathbf{x}_1,\cdots,\mathbf{x}_S)$$
where $$$\mathbf{y}_{SMS}^{\mathbf{\Omega}}$$$ is acquired SMS k-space, $$$\mathbf{\Omega}$$$ is sampling pattern, S is number of slices, $$$\mathbf{E}_{i}^{\mathbf{\Omega}}$$$ is the multi-coil encoding operator of the i^th slice, $$$\mathbf{x}_i$$$ is the i^th slice image. Note the first term enforces data consistency (DC) and and $$$\cal{R}(\cdot)$$$ is a regularizer. There are various iterative techniques that decouple the DC and regularizer into a series of sub-problems⁸. Physics-guided DL reconstruction unrolls such iterative processes for a fixed number of iterations³. Then the regularization sub-problem is implicitly solved via neural networks, while the DC sub-problem is solved using conventional linear methods.

The lack of reference training data in fMRI studies inhibits conventional supervised training used for DL methods. However, a self-supervised deep learning strategy (SSDU) that does not require fully-sampled data for training was recently proposed, showing similar performance to supervised learning⁷. SSDU^7,9 divides the acquired k-space $$$\mathbf{\Omega}$$$ into two sets, where one is used in DC units and the other to define k-space loss. In this work, we used multi-mask SSDU⁹ with 3 masks, and Adam optimizer with learning rate$$$=5\times10^{-4}$$$, an $$$\ell_{1}-\ell_{2}$$$ training loss³ and 100 epochs. DC units used conjugate-gradient and the regularizer used a ResNet⁷. Training was performed on 17 slab groups from 6 subjects. Only one time-frame per subject was used, thus no temporal correlations were exploited by DL reconstruction. Testing was performed on the whole volume and time series of 4 different subjects. A schematic of the implementation is shown in Figure 1.

IMAGING EXPERIMENTS:

The raw k-space data for training and testing of the DL reconstruction was acquired at 7T (Siemens Magnetom) for retinotopic imaging as part of the 7T Human Connectome Project^10,11. For each subject, six 5min acquisitions were obtained with standard retinotopic mapping experiments. Specifically, the first two runs involved a rotating wedge (RETCCW, RETCW), the second two runs involved an expanding or contracting ring (RETEXP, RETCON), and the last two runs involved a moving bar (RETBAR1, RETBAR2). A 5-fold SMS and 2-fold in-plane acceleration was used with a 1.6mm isotropic resolution and 1s TR.

DATA ANALYSIS:
During the testing of the DL reconstruction, the rotating wedge (RETCCW) scan from 4 subjects, unseen by the network, was evaluated for their tSNR (calculated by mean/standard deviation of a time series) and functional response. The analyzePRF¹² MATLAB toolbox was used for performing population receptive field (pRF) analyses to fMRI data and quantified with Pearson's linear correlation coefficient. Temporal stability of the reconstructed time-series was qualitatively evaluated with the tSNR (variance normalized by the mean). No motion or distortion correction was applied to reconstructed series.

RESULTS

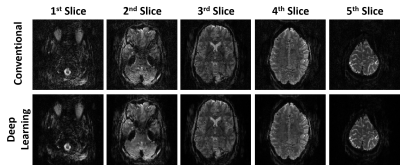
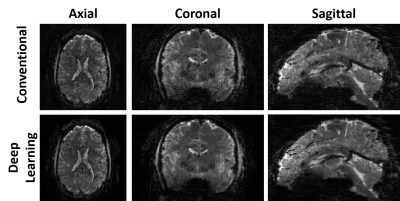
Fig. 2 shows reconstructed images using conventional and self-supervised DL reconstructions. Proposed DL reconstruction visibly reduces noise and removes residual aliasing artifacts observed in thalamus region (3^rd slice) with conventional reconstruction.
Fig. 3 depicts axial, coronal and sagittal slices of another subject reconstructed with conventional and self-supervised DL reconstructions. DL reconstruction substantially reduces noise in thalamus region compared to conventional method.
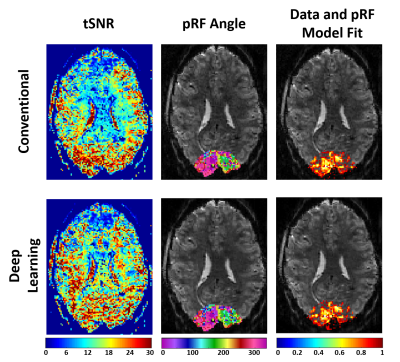
Fig. 4. shows the tSNR, estimated population receptive field for the RETCCW, and the correlation between time-series data and the pRF model for the conventional and the self-supervised DL reconstructions. The DL reconstruction increases the tSNR in the center of the brain compared to the conventional reconstruction. The estimated population receptive field (pRF) model in the occipital lope is similar for the two techniques, reflecting that the DL reconstruction does not remove subtle temporal effects.

DISCUSSION AND CONCLUSION

In this study, we evaluated a self-supervised physics-guided deep learning reconstruction for highly-accelerated HCP-style fMRI. Although, the conventional reconstruction provided sufficient baseline image quality for this particular acquisition, DL reconstruction still reduced residual artifacts, and improved the tSNR. The fMRI analysis led to similar results between two techniques, showing that DL reconstruction did not alter the temporal effects or functional spatial precision. Following this preliminary study to establish the feasibility of DL methods for accelerated fMRI, further investigations at higher acceleration rates are warranted to harness the full potential of the proposed DL reconstruction.

Acknowledgements

Grant support: NIH, Grant numbers: P30NS076408, R01HL153146, U01EB025144, P41EB027061; NSF, Grant number: CAREER CCF-1651825.