Introduction

Recently, unrolled neural networks (UNNs) have been shown to improve reconstruction over conventional Parallel Imaging Compressed Sensing (PI-CS) methods for Cartesian-based images ^1–5. However, there are two limitations of the method for Non-Cartesian dynamic image reconstruction. First, Non-Cartesian reconstruction typically requires complex operations in a single iteration and often takes many iterations to converge, which may be problematic due to limited GPU memory ⁶. Second, commonly used simple networks based on CNN ^1,7 or RNN ² are insufficient to learn the detailed underlying dynamics of the moving images.
In this work, we propose two methods to overcome these limitations. First, we use a memory efficient method for training, also known as gradient checkpointing ⁸. This can greatly alleviate GPU memory constraints without modifying the network architecture. Second, we propose a novel network architecture based on Convolutional LSTM, which has been demonstrated to be effective for training spatiotemporal data ⁹. We tested our method for reconstruction of radial cardiac cine imaging on synthetized dataset.

Methods

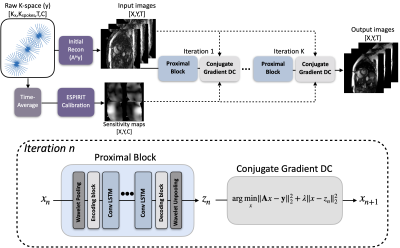
1. UNN architecture for Non-Cartesian dynamic image reconstruction
The UNN (Fig. 1) is designed to solve the following inverse problem
$$b=A(x) +n \ \ \ \ \ [Eq.1] $$
$$arg\min_{x} \parallel{Ax-b}\parallel_2^2+\lambda R(x) \ \ \ \ \ [Eq.2] $$
where A is the non-Cartesian sampling operator involving composition of a non-uniform Fourier transform (NUFFT), undersampling trajectory, sensitivity maps. The problem can be formulated as a non-convex optimization problem (Eq.2) involving a regularizer whose proximal operators can be parameterized by a neural network. We used the MoDL framework ⁴, which iterates between proximal steps and data-consistency steps with conjugate-gradient descent. For the NUFFT, we use the GPU-based implementation from the SigPy library ¹⁰, which is compatible with PyTorch ¹¹. The network is implemented in PyTorch, and training is performed on an NVIDIA 1080 Ti 11GB graphics card.

2. Memory Efficient Training
Recently, a memory-efficient training scheme was introduced for training the UNN ⁸, In this study, we used the gradient checkpointing scheme ¹², mentioned in the literature. This method saves only the intermediate inputs and outputs of every unrolled blocks rather than the whole computational graph during the forward step to save substantial memory. With this, much flexible number of unrolls (up to 50) can be used to train the network, while conventional training method only allow few numbers (up to 5) of unrolls.

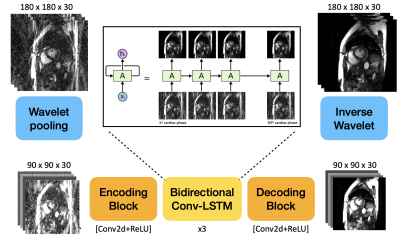
3. Conv-LSTM based Network
For sequence modeling, LSTM is a special RNN structure that has proven stable and powerful for modeling long-range dependencies ¹³. Conv-LSTM exchanges internal matrix multiplication in LSTM with convolution operations and enables effective modeling of spatiotemporal features ⁹.
In order to increase the receptive field, we first pool the image by a factor of 2 using first order wavelet decomposition, also known as wavelet pooling ¹⁴. Then the resulting image is further encoded by a sequence of Conv2D + ReLU to produce high dimensional features for Conv-LSTM module. Then the feature images are symmetrically decoded and recovered to the original matrix size.

4. Dataset
Fully sampled bSSFP 2D cardiac Cartesian CINE data used in ¹ is used to generate synthetic radial cine data. In the dataset, 190 slices were acquired from 15 volunteers at different cardiac views and slice locations on 1.5T and 3.0T GE (Waukesha, WI) scanners.The multi-coil radial k-space measurement was synthetized by multiplying the sensitivity maps and sampling with the tiny-golden angle trajectory ¹⁵. The resulting size of the k-space data is 180 × 282 × 30 × 8 (Nreadout × Nspoke × Nphase × Ncoil). Input data is further under-sampled by approximately 18-fold acceleration, resulting in 180 × 15 × 30 × 8. Training was performed on synthetic dataset from 12 subjects and testing was performed on remaining subjects.

5. Evaluation
We compare four different methods with respect to standard image quality metrics (PSNR, SSIM). Moreover, the consumption of GPU memory and inference time were compared.
1) PI-CS ^15,16: PI-CS method using temporal total-variation regularization.
2) Short CNN: UNN with five iterations containing 2D spatial and 1D temporal residual networks with parameters shown in ¹.
3) Long CNN: UNN with ten iterations containing 2D spatial and 1D temporal residual networks.
4) Proposed: UNN with ten iterations containing Conv-LSTM based network.

Results

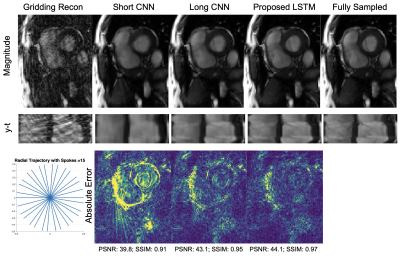
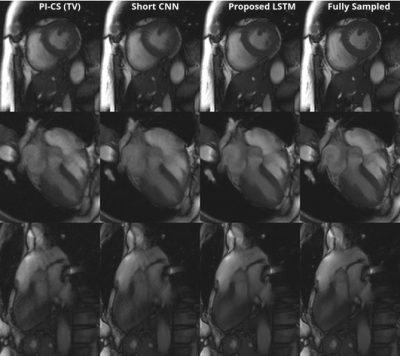
Figure 3 shows a representative comparison of Gridding, Short CNN, Long CNN, and Proposed LSTM. Resulting images from the "proposed LSTM" outperforms with sharper details, higher PSNR, higher SSIM compared to other methods with the same training epochs.
Figure 4 shows animation result from PI-CS, Short CNN, and Proposed LSTM for three different cardiac views. Sharper edges and less streaking artifact can be seen on the reconstructed result using the proposed method.
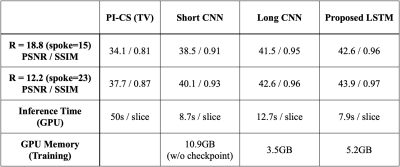
Figure 5 shows the quantitative values for each methods. This shows that our method provides the best reconstruction without elongating inference time or burdening GPU memory.

Conclusions & Discussion

In this work, we presented two methods to improve conventional UNN for Non-Cartesian CINE images. With the addition of these, we were able to reconstruct images with higher image quality. The method will be further evaluated for prospectively sampled cardiac cine images as well.

Acknowledgements

NIH R01 EB009690, NIH R01 EB026136, and GE Healthcare