0446
Frobenius optimization of tensor-valued diffusion sampling schemes1Random Walk Imaging AB, Lund, Sweden
Synopsis
Tensor-valued diffusion encoding has allowed for increased specificity in diffusion MRI, probing the diffusion patterns of water molecules in vivo along new dimensions. From an intuitive standpoint, a versatile sampling scheme should be sensitive to a diverse set of diffusion profiles in any given voxel. However, while optimization strategies based on electrostatic repulsion achieve this for conventional diffusion sampling scheme, no equivalent optimization exists for tensor-valued diffusion data. In this work, we derive an optimization strategy based on maximizing the Frobenius distance between b-tensors. Its evaluation in silico demonstrates that it increases the accuracy of diffusion tensor distribution imaging.
Introduction
Finding its roots in the field of physical chemistry,1,2 tensor-valued diffusion encoding3-5 has allowed to enhance the specificity of diffusion MRI by acquiring complementary pieces of diffusion information. Tensor-valued acquisition schemes are characterized by b-tensors $$$\mathbf{b}$$$ varying in terms of trace (b-value) $$$b=\mathrm{Tr}(\mathbf{b})$$$, shape $$$b_\Delta$$$ and orientation $$$(\Theta,\Phi)$$$. In particular, the b-tensor shape6,7 $$$b_\Delta$$$ reports on the type of diffusion pattern probed by a given b-tensor: while planar b-tensors ($$$b_\Delta=-0.5$$$) probe diffusion in the plane perpendicular to their orientation $$$(\Theta,\Phi)$$$, spherical b-tensors ($$$b_\Delta=0$$$) probe isotropic diffusion patterns and conventional linear b-tensors ($$$b_\Delta=1$$$) probe diffusion along their orientation $$$(\Theta,\Phi)$$$.Intuitively, a versatile sampling scheme should yield diffusion signals sensitized to a diverse set of diffusion profiles. For conventional diffusion sampling schemes made of linear b-tensors ($$$b_\Delta=1$$$), optimization protocols exist to ensure diversity in orientation $$$(\Theta,\Phi)$$$ within/across shells of fixed b-value (b-shells) via electrostatic repulsion.8,9 For tensor-valued diffusion sampling schemes, recent optimization strategies have maximized precision in model parameter estimations10 and have decomposed the tensor-valued diffusion signal in terms of basis functions.11 However, a tensor-valued optimization scheme favoring the aforementioned "diversity" concept (i.e. akin to conventional electrostatic repulsion) has yet to be proposed.
Theory
Maximizing diversity:A natural distance between two real symmetric diffusion tensors (such as b-tensors), $$$\mathbf{b}$$$ and $$$\mathbf{b}^\prime$$$, is given by the Frobenius distance$$d_\mathrm{F}(\mathbf{b},\mathbf{b}^\prime)=\sqrt{\mathrm{Tr}((\mathbf{b}-\mathbf{b}^\prime)^2)}\,.$$In terms of the trace $$$b^{(\prime)}$$$, normalized anisotropy $$$b_\Delta^{(\prime)}$$$ and orientation $$$(\Theta^{(\prime)},\Phi^{(\prime)})$$$, the squared Frobenius distance writes$$d_\mathrm{F}^2=\frac{1}{3}\left[b^2(1+2b_\Delta^2)+b^{\prime\,2}(1+2b_\Delta^{\prime\,2})+2bb^\prime(b_{\Delta}b_\Delta^\prime-1)\right]-2bb^{\prime}b_{\Delta}b_\Delta^\prime\cos^2\beta\,,$$where $$$\beta$$$ denotes the shortest angle between the principal axes of $$$\mathbf{b}$$$ and $$$\mathbf{b}^\prime$$$. Computing $$$d_\mathrm{F}$$$ between two b-tensors differing along only one dimension ($$$b$$$, $$$b_\Delta$$$ or $$$\beta$$$), $$$d_\mathrm{F}$$$ grows with $$$\vert b-b^\prime\vert$$$, $$$\vert b_\Delta-b_\Delta^\prime\vert$$$ and $$$\vert\sin\beta\vert$$$. In the general case, $$$d_\mathrm{F}$$$ is sensitive to any type of difference between two b-tensors and can thus be maximized within a given sampling scheme to maximize the diversity of probed b-tensors, equivalent to maximizing the diversity of probed diffusion patterns during the acquisition protocol. Spherical b-tensors, only characterized by their trace, are left aside below to focus on less trivial directional b-tensors.
Gradient-descent minimization:
Analogously to Refs.[8,9], the proposed maximization of $$$d_\mathrm{F}$$$ corresponds to minimizing the force$$f_\mathrm{F}=\frac{1}{\delta_\mathrm{F}^2}=\frac{1}{b^2(1+2b_\Delta^2)+b^{\prime\,2}(1+2b_\Delta^{\prime\,2})+2bb^\prime(b_{\Delta}b_\Delta^\prime-1)-6bb^{\prime}b_{\Delta}b_\Delta^\prime\cos^2\beta}\,,$$where $$$\delta_\mathrm{F}=3d_\mathrm{F}$$$ was chosen for simplicity. Such minimization can be achieved via gradient descent. The gradients of $$$f_\mathrm{F}$$$ in the $$$b$$$ and $$$b_\Delta$$$ dimensions lead to trivial results, i.e. maximizing $$$b$$$, and pushing any b-tensor with $$$b_\Delta<0$$$ toward $$$b_\Delta=-0.5$$$ and pushing any b-tensor with $$$b_\Delta>0$$$ toward $$$b_\Delta=1$$$ (all these cases ultimately maximize $$$d_\mathrm{F}$$$). This implies that the proposed optimization requires fixed b-shells and fixed b-shapes $$$b_\Delta$$$ for each b-shell. However, the $$$\beta$$$ dimension is non-trivial, as the gradient of $$$f_\mathrm{F}$$$ in this dimension writes$$\left.\nabla f_\mathrm{F}\right\vert_{\beta}=\frac{{\partial}f_\mathrm{F}}{\partial\beta}\,\mathbf{u}_\beta=-\frac{6bb^{\prime}b_{\Delta}b_\Delta^\prime}{\delta_\mathrm{F}^4}\,\sin(2\beta)\;\mathbf{u}_\beta\,,$$where $$$\mathbf{u}_\beta=\mathbf{u}\times(\mathbf{u}\times\mathbf{u}^\prime)/\vert\sin\beta\vert$$$, with $$$\mathbf{u}^{(\prime)}=(\sin\Theta^{(\prime)}\cos\Phi^{(\prime)},\sin\Theta^{(\prime)}\sin\Phi^{(\prime)},\cos\Theta^{(\prime)})$$$ and the cross product "$$$\times$$$". Unlike the electrostatic gradient of Refs.[8,9], the above Frobenius gradient naturally depends on the b-values and b-shapes of the considered b-tensors, and can therefore be used to optimize the entire sampling scheme at once. However, note that this optimization requires to recast the $$$b_\Delta$$$ space from $$$[-0.5,1]$$$ onto $$$[-0.5,0.5]$$$ to make it symmetric around $$$0$$$. Indeed, this recasting prevents linear tensors ($$$b_\Delta=1$$$) from consistently maximizing $$$d_\mathrm{F}$$$, favoring a $$$b_\Delta$$$ mixing.
Frobenius optimization:
The Frobenius optimization consists in:
- providing a set of b-shells $$$\{b_1,b_2,\dots\}$$$ with the numbers of desired b-tensors per shell $$$\{N_{b_1},N_{b_2},\dots\}$$$, and the desired directional b-shapes per shell $$$\{[{b_\Delta}_1,{b_\Delta}_2,\dots]_{b_1},[{b_\Delta}_1,{b_\Delta}_2,\dots]_{b_2},\dots\}$$$ (note that the number of b-tensors with a given shape $$$b_\Delta$$$ is not provided here).
- exploring all combinations of b-tensor shapes per shell and across shells, starting from a random direction set for each combination.
- running the gradient-descent minimization using the above expression for $$$\left.\nabla f_\mathrm{F}\right\vert_{\beta}$$$ to optimize the direction sets of each combination across all b-shells, thereby minimizing $$$f_\mathrm{F}$$$.
- keeping the optimized combination with lowest $$$f_\mathrm{F}$$$.
In silico evaluation
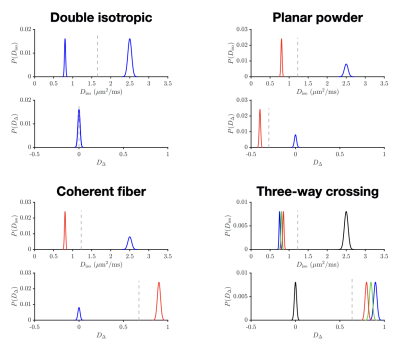
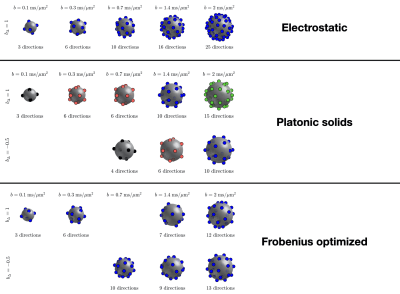
To assess the potential of Frobenius-optimized acquisition schemes, we investigate the accuracy and precision of diffusion tensor distribution imaging (DTD)12 within the four in silico systems presented in Figure 1. DTD is a versatile inversion technique for tensor-valued diffusion data that characterizes each voxel content in terms of a nonparametric diffusion tensor distribution.13 It is, however, susceptible to noise, mostly in terms of estimation biases.14For each aforementioned system, 50 Rician noise realizations at a clinically relevant signal-to-noise ratio of 30 are generated for each 60-point acquisition sampling scheme presented in Figure 2, namely:
- a sampling scheme based on electrostatic repulsion.8,9
- a sampling scheme based on platonic solids.15,16
- a comparable Frobenius-optimized sampling scheme.
Results and discussion
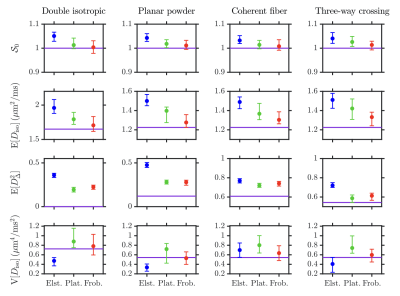
Figure 3 presents four DTD statistical descriptors estimated in the above numerical systems:- the non diffusion-weighted signal $$$\mathcal{S}_0$$$.
- the mean diffusivity $$$\mathrm{E}[D_\mathrm{iso}]$$$.
- the squared normalized anisotropy $$$\mathrm{E}[D_\Delta^2]$$$.
- the variance of isotropic diffusivities $$$\mathrm{V}[D_\mathrm{iso}]$$$.
Conclusion
Frobenius optimization, by maximizing the diversity of diffusion profiles probed by the acquired sampling scheme, shows potential for future enhancements of multidimensional diffusion signal inversions.Acknowledgements
We would like to thank Dr. Filip Szczepankiewicz for our fruitful discussions.References
1. E. R. Andrew et al., Nature 183, 1802-1803 (1959).
2. K. Schmidt-Rohr and H. W. Spiess, Multi-dimensional Solid-state NMRand Polymers, Academic Press, San Diego (1994).
3. D. Topgaard, Multidimensional diffusion MRI, Journal of Magnetic Resonance 275, 98-113 (2017).
4. H. Lundell and S. Lasič, Diffusion encoding with general gradient waveforms. In: Topgaard D., (Ed.). Advanced Diffusion Encoding Methods in MRI. Cambridge, UK: Royal Society of Chemistry, (2020).
5. A. Reymbaut, Diffusion Anisotropy and Tensor-valued Encoding. In: Topgaard D., (Ed.). Advanced Diffusion Encoding Methods in MRI. Cambridge, UK: Royal Society of Chemistry, (2020).
6. T.E. Conturo et al., Encoding of anisotropic diffusion with tetrahedral gradients: A general mathematical diffusion formalism and experimental results, Magnetic Resonance in Medicine 35, 399-412 (1996).
7. S. Eriksson et al., NMR diffusion-encoding with axial symmetry and variable anisotropy: distinguishing between prolate and oblate microscopic diffusion tensors with unknown orientation distribution, Journal of Chemical Physics 142, 104201 (2015).
8. D. K. Jones et al., Optimal strategies for measuring diffusion in anisotropic systems by magnetic resonance imaging. Magnetic Resonance in Medicine 42, 515-525 (1999).
9. E. Caruyer et al., Design of multishell sampling schemes with uniform coverage in diffusion MRI, Magnetic Resonance in Medicine 69, 1534 (2013).
10. S. Coelho et al., Optimal Experimental Design for Biophysical Modelling in Multidimensional Diffusion MRI. I D. Shen, T. Liu, T. M. Peters, L. H. Staib, C. Essert, S. Zhou, P-T. Yap, & A. Khan (red.), Medical Image Computing and Computer Assisted Intervention – MICCAI 2019: Proceedings (Bind III, s. 617-625). Springer. Lecture Notes in Computer Science Bind 11766. (2019).
11. A. P. Bates et al., A 4D basis and sampling scheme for the tensor encoded multi-dimensional diffusion MRI signal, IEEE Signal Process. Lett. (2020).
12. D. Topgaard, Diffusion tensor distribution imaging, NMR in Biomedicine 32, e4066 (2019).
13. B. Jian et al., A novel tensor distribution model for the diffusion-weighted MR signal, Neuroimage 37, 1, 164-176 (2007).
14. A. Reymbaut et al., Accuracy and precision of statistical descriptors obtained from multidimensional diffusion signal inversion algorithms, NMR in Biomedicine 33, e4267 (2020).
15. C.-F. Westin et al., Q-space trajectory imaging for multidimensional diffusion MRI of the human brain, Neuroimage 135, 345-362 (2016).
16. F. Szczepankiewicz et al., Linear, planar and spherical tensor-valued diffusion MRI data by free waveform encoding in healthy brain, water, oil and liquid crystals, Data Brief 25, 104208 (2019).
Figures