0444

Algebraic reconstruction of missing data in zero echo time MRI with pulse profile encoding (PPE-ZTE)

Romain Froidevaux¹, Markus Weiger¹, and Klaas Paul Pruessmann¹
¹Institute for Biomedical Engineering, ETH Zurich and University of Zurich, Zurich, Switzerland

Synopsis

Short-T₂ imaging needs immediate and rapid encoding, as provided by zero echo time (ZTE) MRI. However, in ZTE, excitation and early encoding occur simultaneously and preclude data acquisition in the k-space center, leading to local undersampling or gap. One way of retrieving the missing data involves algebraic reconstruction, but it is limited to small gaps and thus requires short RF pulses that restrain achievable SNR and contrast options. Here, we demonstrate a method for algebraic reconstruction of large gaps, based on the knowledge of excitation pulses. It enables the use of longer pulses and overcomes ZTE flip angle limitations.

Introduction

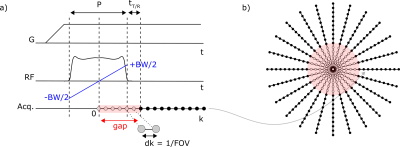
MRI of tissues with fast transverse relaxation times T₂ or T₂*, such as bone or myelin, requires dedicated pulse sequences capable of acquiring the MR signal quickly after radiofrequency (RF) excitation (1,2). An efficient method to do so is zero echo time (ZTE) imaging (3), in which the radial readout gradient is followed by spin excitation, and data is acquired as soon as possible after RF transmit-receive (T/R) switching (Fig. 1a). This sequence timing involves an RF dead time determined in part by the duration of the RF pulse, which precludes data acquisition in the k-space center (Fig. 1b). If pulses are short enough, the missed data may be retrieved algebraically, but only if the gap does not exceed about 3 Nyquist dwells, dk (= 1/FOV with FOV the field of view) (4). However, due to finite available RF power, pulse amplitudes and hence flip angles are limited, potentially restricting SNR and contrast options. If longer pulses are needed, other techniques could be used, such as PETRA (5), WASPI (6) or HYFI (7). However, they all require additional data acquisition with changes in readout gradient strength, which may lead to higher acoustic noise, lower SNR efficiency or propensity to short-T₂ related artefacts (8). In this work, we demonstrate an alternative method called pulse profile encoded ZTE (PPE-ZTE) that allows algebraic reconstruction of ZTE datasets acquired with long RF-pulses. It relies on the knowledge of the spatial profile of the excitation pulse and its introduction in the ZTE signal model. In this way, larger flip angles can be realized, thus improving SNR efficiency and permitting increased T₁ contrast in ZTE images, which are commonly proton-density weighted. Moreover, in PPE-ZTE, the readout gradient strength is kept constant, hence creating minimal acoustic noise.

Theory

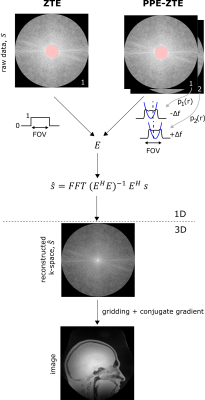
To get sufficiently independent data, PPE-ZTE requires two separate acquisitions of the k-space support using frequency-swept RF pulses differing only by small off-resonances $$$+\Delta f$$$ and $$$-\Delta f$$$ respectively (Fig. 2). In this way, the approximately quadratic phase of the pulse profile is shifted proportionally to $$$\Delta f$$$ while the magnitude and hence the flip angle remain constant over the FOV. Reconstruction of a 1D projection in PPE-ZTE is similar to ZTE, with the exception that the pulse profiles, $$$p_l (r_m )$$$ , are introduced in the encoding matrix E (Fig. 2):
$$E_{(l,m),n}=e^{(i 2\pi k_m r_n)}\cdot p_l(r_n)$$
where k and r span k-space and image space respectively.

Methods

Imaging experiments were performed on a 3T Philips Achieva scanner complemented with a high-performance insert gradient (9). The RF signal was created with a Bruker amplifier (BLA-1000) with maximum output power of 1000 W. Either hard or sweep pulses were used for excitation (10). Short-T₂ optimized hardware included: T/R switches capable of switching in about 3 µs (11), an 1H-free birdcage coil (12) and a spectrometer with up to 4 MHz acquisition bandwidth and a corresponding filter group delay of about 1 µs (13). A water bottle was used as a phantom, doped with CuSO₄ and H₂SO₄ to match physiological relaxation times. The shape of the RF pulses was measured with a pickup coil placed near the birdcage coil. The total scan time of ZTE and PPE-ZTE images was matched by adapting the number of averages.

Results

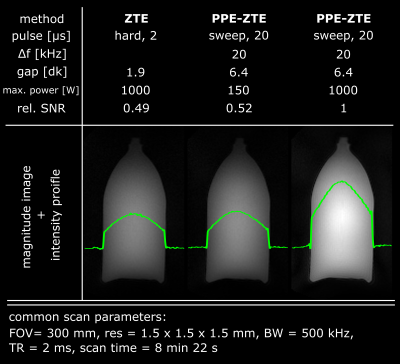
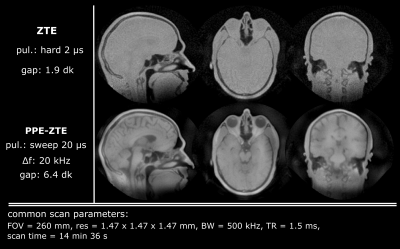
The robustness with respect to gap size of PPE-ZTE is demonstrated in Figure 3. As pulse length increases, model violations such as noise or aliased signals create serious artefacts in conventional ZTE images at large gap (≥4dk). However, PPE-ZTE preserves images quality, independent from the pulse length. Figure 4 illustrates improved SNR with PPE-ZTE. In this example, the signal available in ZTE is limited due to the necessity of using short pulses (max. 2 µs for an imaging bandwidth, BW = 500 kHz). Using longer pulses, the same image quality is obtained in PPE-ZTE with substantially less peak power. Finally, with longer pulses and same power, PPE-ZTE is able to create larger flip angles, increasing signal and SNR by a factor 2 for equal scan time. In Figure 5, conventional ZTE images with 500 kHz bandwidth are limited to proton-density contrast. However, with PPE-ZTE, introducing T₁ contrast is enabled due to the larger available flip angles.

Discussion

Utilizing the encoding properties of the RF pulse in PPE-ZTE compensates for the data lost during excitation and thus renders image quality of algebraic reconstructions almost independent of the pulse duration. However, it is still limited by the T/R switching time (including filter group delays), t_T/R. As a rule of thumb, t_T/R should not exceed 2-3 dk. Hence, for the current setup with t_T/R 4µs, the achievable bandwidth is limited to 500 kHz. However, current developments towards even faster T/R switching (14) hold promise for PPE-ZTE at further increased bandwidths.

Conclusion

We demonstrated algebraic reconstruction of ZTE datasets with large k-space gaps by employing the PPE-ZTE technique. As opposed to conventional ZTE, image fidelity has only a minor dependence on pulse duration. Hence, significant improvements in SNR efficiency as well as T₁ contrast become possible, even at high imaging bandwidth. Moreover, compared to approaches using gap filling, PPE-ZTE does not require changes in gradient strength and therefore produces negligible acoustic noise.

Acknowledgements

No acknowledgement found.

References

(1) Bydder GM. Imaging of Short and Ultrashort T2 and T2* Components of Tissues, Fluids, and Materials in the Body Using Clinical Magnetic Resonance Systems. EMagRes 2012;1:811–22.

(2) Weiger M, Pruessmann KP. Short-T2 MRI: Principles and recent advances. Prog Nucl Magn Reson Spectrosc 2019;114–115:237–70.

(3) Weiger M, Pruessmann KP. MRI with zero echo time. Encycl Magn Reson 2012;1:311–22.

(4) Weiger M, Brunner DO, Tabbert M, Pavan M, Schmid T, Pruessmann KP. Exploring the bandwidth limits of ZTE imaging: Spatial response, out-of-band signals, and noise propagation. Magn Reson Med 2015;74:1236–47.

(5) Grodzki DM, Jakob PM, Heismann B. Ultrashort echo time imaging using pointwise encoding time reduction with radial acquisition (PETRA). Magn Reson Med 2012;67:510–8.

(6) Wu Y, Dai G, Ackerman JL, Hrovat MI, Glimcher MJ, Snyder BD, Nazarian A, Chesler D a. Water- and fat-suppressed proton projection MRI (WASPI) of rat femur bone. Magn Reson Med 2007;57:554–67.

(7) Froidevaux R, Weiger M, Roesler M, Brunner D, Pruessmann K. HYFI: Hybrid filling of the dead-time gap for faster zero echo time imaging. MedRxiv 2020. https://doi.org/10.1101/2020.06.16.20132704

(8) Froidevaux R, Weiger M, Brunner DO, Dietrich BE, Wilm BJ, Pruessmann KP. Filling the dead-time gap in zero echo time MRI: Principles compared. Magn Reson Med 2018;79:2036–45.

(9) Weiger M, Overweg J, Rösler MB, Froidevaux R, Hennel F, Wilm BJ, Penn A, Sturzenegger U, Schuth W, Mathlener M, et al. A high-performance gradient insert for rapid and short-T 2 imaging at full duty cycle. Magn Reson Med 2018;79:3256–66.

(10) Weiger M, Pruessmann KP, Hennel F. MRI with zero echo time: Hard versus sweep pulse excitation. Magn Reson Med 2011;66:379–89.

(11) Brunner DO, Furrer L, Weiger M, Baumberger W, Schmid T, Reber J, Dietrich BE, Wilm BJ, Froidevaux R, Pruessmann KP. Symmetrically biased T/R switches for NMR and MRI with microsecond dead time. J Magn Reson 2016;263:147–55.

(12) Rösler MB, Weiger M, Brunner DO, Schmid T, Pruessmann KP. An RF birdcage coil designed for an insert gradient coil dedicated to short-T2 MRI. Proc 26th Annu Meet ISMRM, Honolulu 2017:2668.

(13) Dietrich BE, Brunner DO, Wilm BJ, BarmeT C, Gross S, Kasper L, Haeberlin M, Schmid T, Vannesjo SJ, Pruessmann KP. A field camera for MR sequence monitoring and system analysis. Magn Reson Med 2016;75:1831–40.

(14) Christoph Michael Schildknecht, Klaas Paul Pruessmann, Gallium nitride MOSFETs enable transmit-receive switching in less than 100ns, Submitted to ISMRM 2021

Figures

Fig. 1: ZTE pulse sequence. a) After ramping up the gradient G, RF excitation is performed by using either short block pulses, or, in case of limited RF power, longer sweep pulses (with the frequency swept over the imaging bandwidth, BW (blue line)). Data is acquired after the dead time gap (red) that includes half the pulse duration P and the transmit-receive switching time t_T/R. b) The 3D k-space support is probed radially. However, due to the gap, data is missing in the k-space center.

Fig. 2: Image reconstruction. ZTE: the raw data s is acquired once and the encoding matrix E is computed assuming that the RF sensitivity is 1 inside the FOV and 0 outside. The missing data is extrapolated by multiplication with the pseudo inverse of E followed by FFT in 1D. Then, gridding is used to reconstruct the 3D image. PPE-ZTE: same, except that: 1) Raw data is acquired twice with pulses differing only by an off-resonance . 2) The knowledge of the pulse profiles p(r) is included in E.

Fig. 3: ZTE MRI of a water bottle using long RF excitation pulses. In conventional ZTE, for gaps ≥ 4 dk, amplification of noise and aliased signal create artifacts that dominate the images. However, PPE-ZTE preserves image quality, even with long sweep pulses. The linear grey-scaling is normalized to the maximum of each image separately.

Fig. 4: PPE-ZTE MRI of a water bottle with large flip angles. Left: ZTE MRI with maximum power and block pulse duration. Middle: PPE-ZTE MRI with longer sweep pulse and lower power chosen to match the flip angle of the ZTE acquisition. Right: PPE-ZTE MRI with longer sweep pulse and maximum power leading to higher signal and SNR values. The linear grey-scaling is normalized to the maximum of the PPE image in the right column.

Fig. 5: In-vivo PPE-ZTE MRI in the head. ZTE is limited to proton-density contrast due to the low flip angle reached with short block pulses, even at maximum power. However, PPE-ZTE allows the use of longer sweep pulses that create larger flip angles and consequently T1 contrast, in this case mostly between the cerebrospinal fluid and brain tissues. Furthermore, short-T2 signal of the eye lenses stands out against the vitreous body. Remaining low intensity variation are likely to stem from residual model violations.

Proc. Intl. Soc. Mag. Reson. Med. 29 (2021)

0444