Introduction

Diffusion-weighted imaging (DWI) is an important contrast in diagnosing and staging of tumors^1,2 which is often based on single-shot EPI (ssh-EPI). In comparison, multi-shot EPI (msh-EPI) with a 2D-navigator to sense the physiological motion has gained popularity due to the shorter echo train length and reduced geometric distortions^3,4. Another common issue for EPI-based DWI is the presence of fat signal that has large spatial displacements in phase-encoding direction. Conventionally, spectral selective techniques such as SPIR⁵ have been used to suppress fat signals. However, those are prone to fail in regions of high B₀ inhomogeneity⁶. Thus, water/fat separation via chemical-shift encoding might become an effective option⁷. Moreover, due to the fat spectrum’s multipeak profile, fat signals with different resonance frequencies will be spatially shifted to different locations in EPI images. Currently, researches attempted to address these challenges by a combination of chemical-shift encoding and spectral selective fat suppression approaches^8,9. The k-space based algorithm could be another alternative but might suffer from an impractical long reconstruction time¹⁰. Tailored to the EPI, we propose a joint regularized algorithm with a series of shift matrices in image space to time-efficiently estimate accurate water, fat and B₀ maps. In-vivo data were acquired through a TE-shifted navigator-based DW msh-EPI to enable chemical-shift encoding.

Methods

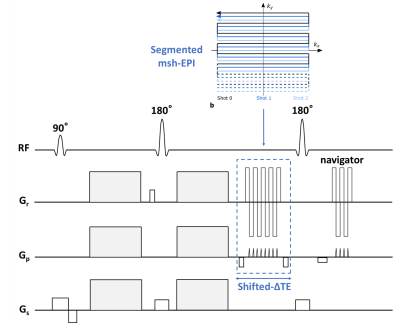
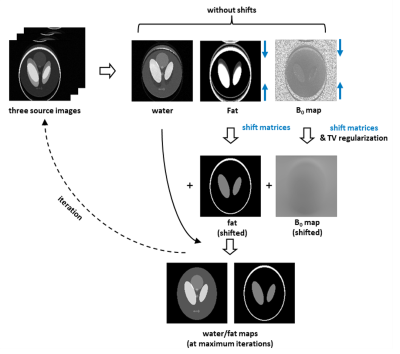
A custom 2D-navigated DW msh-SE-EPI sequence segmented along the phase-encoding direction was complemented to enable time-shifts of the msh-EPI sampling window, depicted in Fig. 1. After data acquisition, N = 3 chemical-shift encoded source images are obtained through IRIS⁴ reconstruction to correct motion-induced physiological phase changes. The different spatial shifts along the phase-encoding direction of the fat components compared to the water signal and the local B₀ value are explicitly taken into account in the signal model:$$S_{n}\left(w(x,y),f(x,y),\varphi_{B}(x,y)\right)=w(x,y)e^{i2\pi\varphi_{B}(x,y)\Delta\mathrm{TE}_{n}}+\sum_{m=1}^{M}\alpha_{m}f\left(x,y-\Delta y_{m}\right)e^{i2\pi\varphi_{B}\left(x,y-\Delta y_{m}\right) \Delta\mathrm{TE}_{n}}e^{i2 \pi\varphi_{F, m}\Delta\mathrm{TE}_{n}}+v_{n}(x, y)$$where $$$w$$$ and $$$f$$$ are the magnitudes of water and fat signals, $$$\Delta\mathrm{TE}_{n}$$$[s] the $$$n$$$-th TE-shifted scan, $$$\varphi_{B}$$$[Hz] the B₀ field at certain $$$(x,y)$$$ and originated $$$(x,y-\Delta y_{m})$$$ locations in phase-encoding direction. Moreover, $$$\alpha_{m}$$$ and $$$\varphi_{F, m}$$$ [Hz] denote the relative weight and resonance frequency for each fat peak $$$m$$$, and $$$v_{n}(x, y)$$$ is complex noise. For water/fat separation, the signal equation poses the following minimization problem:$$\{W,F\}=\underset{\widehat{W},\widehat{F}\in\mathbb{C}^{Q}}{\operatorname{argmin}}\|\hat{A}X-S\|_{2}^{2}$$Where $$$Q$$$ is the number of voxels.$$$S=\left[s_{1}^{1},\ldots,s_{1}^{Q},\ldots,s_{N}^{1},\ldots,s_{N}^{Q}\right]^{T}$$$ and $$$X=[W,F]^{T}=\left[w^{1},\ldots,w^{Q},f^{1},\ldots,f^{Q}\right]^{T}$$$ are vectorized representations of the $$$N$$$ source images and water/fat contents. $$$\hat{A}$$$ is the joint coefficient matrix with two series of shift matrices acting on fat signals and fat associated B₀ map to shift them back to the original location. The B₀ map can be estimated by Gauss-Newton optimization:$$\left\{\Delta\Phi_{B},\Delta W,\Delta F\right\}=\underset{\Delta\varphi_{B}\in\mathbb{R}^{Q}\\ \Delta w,\Delta f\in\mathbb{C}^{Q}}{\operatorname{argmin}}\|\Delta S-\hat{B}\Delta Y\|_{2}^{2}+\lambda TV\left(\Delta\Phi_{B}\right)$$where $$$\Delta Y=\left[\Delta W,\Delta F,\Delta\Phi_{B}\right]^{T}=\left[\Delta w^{1},\ldots,\Delta w^{Q},\Delta f^{1},\ldots,\Delta f^{Q},\Delta \varphi_{B}^{1},\ldots,\Delta\varphi_{B}^{Q}\right]^{T}$$$ and $$$\hat{B}$$$ is the coefficient matrix of the Gauss-Newton search system with shift matrices to shift back $$$\Delta F$$$ and $$$\Delta\Phi_{B}$$$ for each individual peak. $$$TV$$$ is the total variation regularization operator to enforce smoothness of the updated field map error $$$\Delta\Phi_{B}$$$ for the next iteration. Calculation of the two least-square systems are repeated (Fig.2) until the maximum of iterations (e.g.,6) is reached. In addition, for anatomies with severe field inhomogeneities (e.g., head/neck regions), an additional extrapolation step as used for coil-sensitivity maps¹¹ is adopted after half-maximum iterations to give a better initialization for the remaining iterations. A self-calibrated 7-peak fat model based on Ren et al.¹², but at the appropriate TE, was applied¹³. A conventional multipeak IDEAL^6,14 algorithm using the same fat spectrum model was implemented for comparison.
Experiments were conducted in the leg and the head/neck region with 5 subjects on a 3T scanner (Philips, Best, The Netherlands). Each spin-echo DWI experiment was performed with three b-values (0, 300, 600 s/mm²), 6/8 interleaves, TE = 59/53 ms, TR = 2000 ms and at two resolutions: 1.44 x 1.53 x 4 mm³/1.19 x 1.23 x 4 mm³ with acquisition matrices 152 × 160/168 x 162. The three source images were acquired at 0.2/1.0/1.8 ms with respect to the spin echo. For the given matrix sizes, the estimation required 14.9/15.6 s per iteration. In addition, for each measurement another DWI scan was acquired using conventional SPIR for comparison.

Results and Discussion

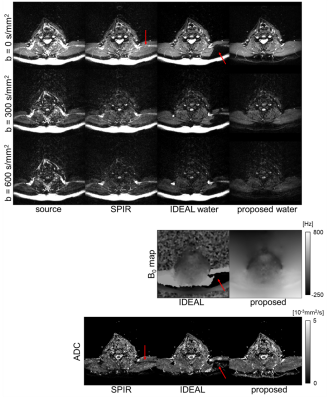
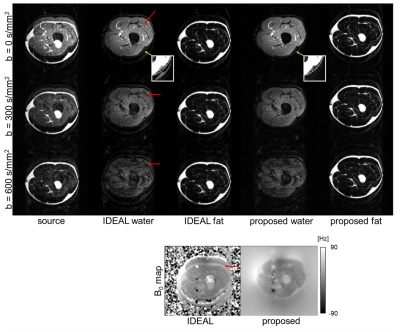
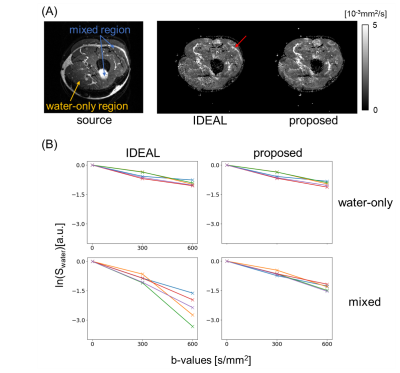
Figure 3 illustrates the DWI results of one subject’s head-neck images of SPIR image and water/B₀ maps estimated from IDEAL/proposed algorithms with ADC calculations. For both SPIR and IDEAL, fat suppression failed in areas with large field inhomogeneities while this was not the case for our proposed algorithm. Figure 4 and 5 show results from IDEAL and our proposed algorithm for one subject’s leg. In Fig.4, the rim-like artifact observed with IDEAL can be eliminated by the proposed algorithm. In Fig.5, the water-only and mixed regions (both water/fat present) were segmented in one source image. The result of the proposed algorithm shows good linearity of the natural logarithm of DWI signals among 5 pixels in both regions, while IDEAL shows nonlinear behaviour in mixed region.

Conclusion

The proposed algorithm provides more reliable water/fat separation and diffusion quantification compared to standard techniques. Future work will include undersampling to support accelerated data acquisition. To further enhance the image quality, fat signal present in 2D-navigators is considered to be eliminated through further approaches¹⁵.

Acknowledgements

The authors would like to acknowledge NWO-TTW (HTSM-17104) for funding this project.