0437

Rapid dynamic speech imaging at 3Tesla using combination of a custom airway coil, variable density spirals and manifold regularization

Rushdi Zahid Rusho¹, Wahidul Alam¹, Abdul Haseeb Ahmed², Stanley J. Kruger³, Mathews Jacob², and Sajan Goud Lingala^1,3
¹Roy J. Carver Department of Biomedical Engineering, The University of Iowa, Iowa City, IA, United States, ²Department of Electrical and Computer Engineering, The University of Iowa, Iowa City, IA, United States, ³Department of Radiology, The University of Iowa, Iowa City, IA, United States

Synopsis

We propose a novel rapid dynamic speech MRI scheme that leverages multi-coil acquisitions from a dedicated 16 channel airway coil, variable density spirals, and manifold regularization. The variable density spirals enables self-navigation to extract the Laplacian manifold matrix from low spatial but high temporal resolution data. Our scheme allows for efficient exploitation of similarities between image frames that are distant in time without the need of explicit binning. We demonstrate robust reconstructions on free running speech data containing complex spatio-temporal dynamics at a temporal resolution of 15 ms/frame.

PURPOSE

Dynamic MRI is a powerful technique to noninvasively assess the complex kinematics of articulators (eg. tongue, velum, lips) during speech. Transform sparsity and low rank based constraints have been previously applied to improve the imaging speed [1], [2]. However, these constraints can get sensitive to motion artifacts, and blurring when there exists large inter-frame motion or large variations in the dynamics such as during free rapid speech, production of trills, and singing. Recently, manifold regularization schemes have shown success in ungated free breathing cardiac MRI applications [3]–[5]. In this work, we propose a scheme that extends manifold regularization to dynamic speech imaging. We also integrate acquisitions from a novel 16 channel dedicated airway coil, and variable density spiral sampling scheme which allows for self extracting navigator information needed for manifold regularization. We show its utility in prospectively enabling rapid imaging of free speech at ~15ms/frame.

METHODS

Acquisition: All our experiments were performed on a 3T GE Premier scanner equipped with high performance gradients (80 mT/m amplitude and 150 mT/m/ms slew rate) using a 16 channel custom airway coil. This coil has two pieces with 5 elements mounted on each of them and placed close to the left and right cheeks; and a third piece with 6 elements placed on the chin and neck. This coil was designed to provide high sensitivity in all upper-airway regions of interest (see Fig. 1). We designed a variable density spiral based gradient echo scheme (spatial resolution: 2.4 mmx2.4 mm; flip angle: 5 degrees; TR=5.1 ms; 27 spiral arms for Nyquist sampling; 329 readout points; readout duration =1.3 ms). The density of sampling along the normalized k-space radius is also shown Fig.1. High density in the center of k-space was employed to self extract navigator information for subsequent reconstruction.
Reconstruction: Fig. 2 illustrates the manifold modeling scheme, where dynamic image frames are modeled as points on a smooth manifold structure in a high dimensional space. Note that image frames that are distant in time but with similar speech postures are mapped as neighboring points on the manifold. This scheme exploits similarity between these neighbors by assigning a larger weight during regularization. Recently, the work in [4] showed the weights can be interpreted as the columns of a graph Laplacian manifold matrix ($$$ \boldsymbol{L}$$$) of dimension $$$ n_{t} \times n_{t} $$$ where $$$n_{t}$$$ are the total number of image frames. We first estimate the $$$ \boldsymbol{L}$$$ matrix from navigator data that correspond to central 60 readout points on the spiral. Next, our reconstruction is posed as:
\begin{equation} \boldsymbol{X}^{*} = \arg \min_{\boldsymbol{X}} \{\|\mathcal{A}(\boldsymbol{X})-\mathbf{b}\|_{F}^{2} + \lambda \hspace{.1cm} trace\hspace{.05cm} (\boldsymbol{X}\boldsymbol{L}\boldsymbol{X}^H) \} \end{equation}
where $$$\boldsymbol{X}$$$ is the dynamic Casorati matrix with dimension $$$n_{x}n_{y}\times n_{t}$$$; $$$\mathbf{b}$$$ is the under-sampled data; $$$\mathcal{A}$$$ is the coil sensitivity and Fourier undersampling operator; $$$\lambda$$$ is a regularization parameter that balances between the constraint and the data consistency term. For faster processing, we perform an eigen decomposition of $$$\boldsymbol{L} = \boldsymbol{V} \boldsymbol{\Sigma} \boldsymbol{V}^T $$$; and use the eigen bases ($$$ \boldsymbol{V}$$$) to reconstruct the spatial weights ($$$ \boldsymbol{U}$$$) as:
\begin{equation} \ \boldsymbol{U}^{*} = \arg \min_{\boldsymbol{U}} \{\|\mathcal{A}(\boldsymbol{U}\boldsymbol{V}^H)-\mathbf{b}\|_{F}^{2} +\lambda \hspace{.05cm}\sum_{i=1}^{k} \sigma_{i} \| \boldsymbol{u_{i}} \|^{2}\}\end{equation}
After reconstructing $$$ \boldsymbol{U}$$$ (dimension of $$$n_{x}n_{y}\times n_{bases}$$$), we finally recover $$$ \boldsymbol{X}$$$ as $$$ \boldsymbol{X}=\boldsymbol{U}\boldsymbol{V}$$$.
Experiments: We imaged 2 volunteers performing two tasks: a) free speech of counting numbers (0-9), and b) repetitions of the phrase za-na-za. The proposed manifold reconstruction was performed using 3 arms/frame that corresponded to ~15 ms/frame. We also compare against a two-step low rank regularization scheme, where the temporal bases in the low rank scheme are obtained from the same navigator data as the manifold based scheme. We empirically determine the choice of 30 basis functions in both the manifold and low rank regularized schemes based on best compromise between artifacts suppression, and motion blurring in both the schemes.

RESULTS

Figure 3 shows the $$$ \boldsymbol{L}$$$ matrix for the za-na-za repetitions and counting tasks. The structure of the $$$ \boldsymbol{L}$$$ matrix clearly depicts how the proposed scheme implicitly exploits similarity amongst distant time frames without any explicit binning strategies. Figure 4 shows the eigen basis functions and the corresponding spatial weights for the two tasks. For the za-na-za repetition task, we observe clear quasi-periodic dynamics in the bases, and for the counting task, we observe more arbitrary dynamics corresponding to free speech. Figure 5 shows the animations and temporal profiles of the manifold scheme and the low rank scheme for the counting task. We observe robust spatio-temporal fidelity and artifact robustness in the proposed scheme as compared to the low rank scheme.

Conclusion

We proposed a self navigated manifold regularized scheme for high speed dynamic MRI of speech at ~15 ms/frame. Our scheme also leveraged variable density spirals and multi-channel acquisitions from a dedicated airway coil. Future work includes exploring additional use of sparsity constraints and use of l1 penalization.

Acknowledgements

This work was conducted on an MRI instrument funded by NIH-S10 instrumentation grant: 1S10OD025025-01.

References

[1] S. G. Lingala, Y. Zhu, Y. Kim, A. Toutios, S. Narayanan, and K. S. Nayak, “A fast and flexible MRI system for the study of dynamic vocal tract shaping,” Magn. Reson. Med., vol. 00, p. n/a-n/a, 2016. [2] M. Fu et al., “High-resolution dynamic speech imaging with joint low-rank and sparsity constraints,” Magn. Reson. Med., 2014. [3] S. Poddar and M. Jacob, “Dynamic MRI Using SmooThness Regularization on Manifolds (SToRM),” IEEE Trans. Med. Imaging, 2016. [4] S. Poddar, Y. Q. Mohsin, D. Ansah, B. Thattaliyath, R. Ashwath, and M. Jacob, “Manifold Recovery Using Kernel Low-Rank Regularization: Application to Dynamic Imaging,” IEEE Trans. Comput. Imaging, 2019. [5] A. H. Ahmed, R. Zhou, Y. Yang, P. Nagpal, M. Salerno, and M. Jacob, “Free-Breathing and Ungated Dynamic MRI Using Navigator-Less Spiral SToRM,” IEEE Trans. Med. Imaging, 2020.

Figures

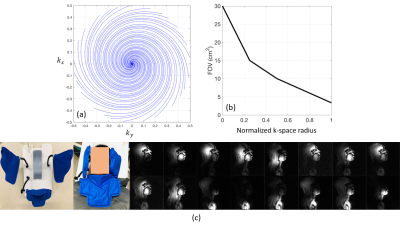
Figure 1: Variable density spiral sampling pattern and the 16-channel novel custom airway coil. (a) shows variable density sampling trajectory in the k_x-k_y plane simulated for full sampling at 2.4x2.4 mm² with 27 spiral arms. (b) shows the FOV v/s normalized k-space radius plot that gives the k-space sampling density. The airway coil is illustrated in (c) without and with the subject: the flexible mounts allow for close conformity of the elements to the subject’s face and neck. Also shown are 16 individual coil images with distinct views generated by inverse NUFFT using 27 spiral arms.

Figure 2: Dynamic images can be modeled as points on a smooth nonlinear manifold embedded in a high dimensional ambient space. This is demonstrated in the dynamic free speech task of serially counting numbers. Similar images are neighbors on the 2D manifold even if they occur at different times (see red and green squares), whereas dissimilar images are distant on the 2D manifold even if they occur consecutively in time. The manifold regularization thus exploits the similarity of points that are close to each other on this manifold.

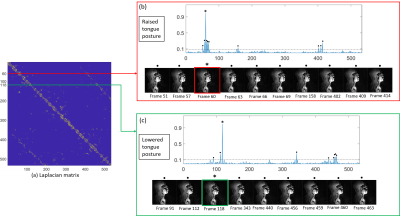
Figure 3: Similar image frames in the dynamic speech task of fluently counting numbers can be identified from the graph Laplacian matrix. (a) shows the graph Laplacian matrix where each row is normalized with respect to the maximum magnitude of the respective rows and thresholded to 10% of the maximum value of each row. Similar tongue postures that do not necessarily occur periodically in time can be identified from the neighborhood relations embedded in the Laplacian matrix. Two different tongue postures: Raised tongue and Lowered tongue are shown in (b) and (c) respectively.

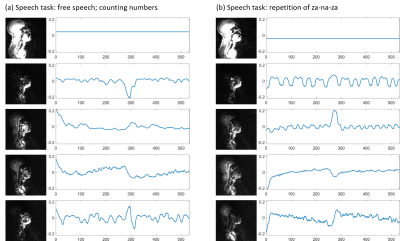
Figure 4: Illustration of spatial coefficients and temporal bases of the speech dynamic MRI for (a) Speech task: free speech; counting numbers, and (b) Speech task: repetition of za-na-za. For each task, the first 5 out of the 30 empirically chosen smallest spatial coefficients and temporal bases are depicted in this figure. It is observed that the temporal bases of the za-na-za task have a more periodic nature than the free speech of counting.

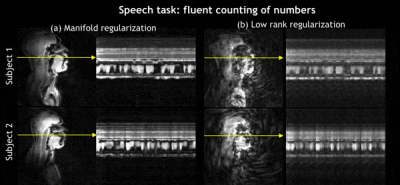
Figure 5 (animation): Comparison of manifold regularization and low rank regularization schemes reconstructed using 3arms/frame (or time resolution of 15 ms). Shown are the dynamic animations and temporal profile cuts from two subjects. We observe good fidelity and under-sampling artifact robustness in the manifold scheme compared to the low rank scheme. This is attributed to efficiently exploiting the similarities in local or distant image frames within the dataset without any explicit binning strategies.

Proc. Intl. Soc. Mag. Reson. Med. 29 (2021)

0437