0410
Exploiting Nerve Membrane Dynamics to Reduce Peripheral Nerve Stimulation using Asymmetric Readout Gradient Waveforms
Natalie G Ferris1,2, Mathias Davids3,4,5, Valerie Klein3,5, Bastien Guérin3,4, and Lawrence L Wald3,4
1Harvard Graduate Program in Biophysics, Harvard University, Cambridge, MA, United States, 2Harvard-MIT Division of Health Sciences and Technology, MIT, Cambridge, MA, United States, 3A. A. Martinos Center for Biomedical Imaging, Department of Radiology, Massachusetts General Hospital, Charlestown, MA, United States, 4Harvard Medical School, Boston, MA, United States, 5Computer Assisted Clinical Medicine, Heidelberg University, Heidelberg, Germany
1Harvard Graduate Program in Biophysics, Harvard University, Cambridge, MA, United States, 2Harvard-MIT Division of Health Sciences and Technology, MIT, Cambridge, MA, United States, 3A. A. Martinos Center for Biomedical Imaging, Department of Radiology, Massachusetts General Hospital, Charlestown, MA, United States, 4Harvard Medical School, Boston, MA, United States, 5Computer Assisted Clinical Medicine, Heidelberg University, Heidelberg, Germany
Synopsis
Peripheral Nerve Stimulation (PNS) limits the use of high-performance gradient systems. We exploit nerve membrane hyperpolarization and depolarization in readout gradient waveform design to achieve a higher gradient moment (area) in a given time without initiating PNS. In a typical symmetric trapezoidal readout waveform, the slew ramps have identical rise times but opposite dB/dt (E-field sign). Asymmetrizing the waveform enables achieving the same gradient moment while emphasizing membrane hyperpolarization over depolarization. The disparate effects of hyperpolarizing and depolarizing pulses are sufficient to impact the nerve’s PNS threshold, potentially increasing the spatial resolution.
Purpose
Peripheral Nerve Stimulation (PNS) from E-fields generated by the rapid switching of strong B-fields has become a limitation in using powerful MRI gradients in humans. The PNS concern is especially acute in fast readout sequences such as EPI, bSSFP etc., where avoiding uncomfortable sensations from PNS requires derating the waveform amplitude or timing1. Most strategies to reduce PNS rely on hardware modifications to reduce the body’s B-field exposure (thus reducing E-fields and PNS), including head-only gradients2,3 or potentially PNS optimized gradient designs4. Here, we explore degrees-of-freedom in readout gradient waveform design to reduce PNS while retaining basic encoding function and timing. We exploit the fundamentally different response to membrane hyperpolarization vs depolarization by asymmetrizing the waveform. Using asymmetric ramp schemes throughout the readout train, we show reduced PNS propensity while maintaining the same k-space coverage (spatial resolution) in a simple nerve model.Methods
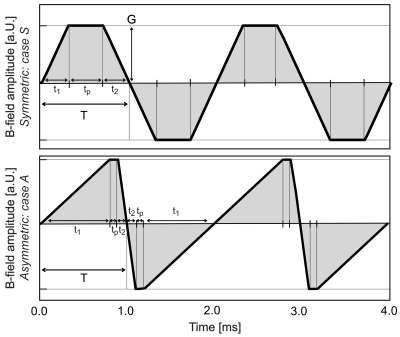
Basics of nerve membrane dynamics: The effect of an E-field on a nerve fiber can be characterized by the activation function, defined as the second spatial derivative of the electric potential along the nerve5. A positive activation function corresponds to depolarization of the membrane (positive charge accumulation), whereas a negative activation function corresponds to hyperpolarization (negative charge accumulation). Depolarization of a nerve is the major driver behind action potential (AP) initiation, whereas hyperpolarization “pre-charges” the membrane making the nerve less susceptible to AP generation.Symmetric and asymmetric waveforms: Figure 1 shows a typical symmetric readout waveform employing slew ramps with identical rise times and slew rates. Therefore, both ramps induce the same E-field patterns with opposite polarity, leading to either depolarization or hyperpolarization respectively. We seek to employ a longer rise time for the more troublesome depolarizing ramp and reduced rise times for the hyperpolarizing ramp. This achieves the same k-space coverage in a fixed time but reduces the depolarizing ramp rate (dB/dt) to reduce positive charge buildup and avoid APs.
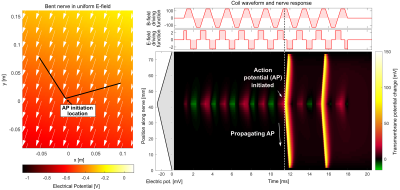
PNS analysis of asymmetric waveforms: We assess the impact of asymmetric waveforms using our electromagnetic-neurodynamic modeling framework6,7. We focus on a simple nerve with a single bend in a homogeneous E-field (Fig. 2). We compute the electric potential along the nerve (by projection and integration of the E-field) as a function of time following the temporal derivative of the gradient waveform (slew rate). The response of the nerve to this spatiotemporal potential is assessed using an electric-circuit neurodynamic model of myelinated nerves (MRG model8). We simulate symmetric and asymmetric waveforms, characterized by two rise times (t1, t2) and a plateau time (tp). The total time per trapezoid (full duration T = t1 + t2 + tp) is kept constant. Figure 2 shows two representative waveform units from which the entire trapezoidal train is composed. For a fixed T, we specify t1 and t2 and then use the PNS modeling framework to determine the smallest readout gradient amplitude G that induces an AP. We give the PNS thresholds both in terms of gradient amplitude G and in k-space.
Results
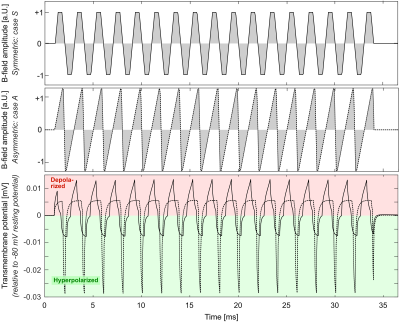
Figure 2 shows the simulation setup (bent nerve in a homogeneous E-field) and the nerve’s transmembrane potential (relative to the resting potential). After initial alternating hyperpolarization (green) and depolarization (red), the nerve fires an AP after roughly 11.5 ms.Figure 3 shows responses of the same nerve segment to a symmetric and two asymmetric trapezoidal waveforms over time for the stimulation location (Fig. 2). All waveforms achieve the same k-space coverage. The symmetric (S) and asymmetric B waveforms induce APs visible by the sudden jump of the transmembrane potential and increases in the sodium and potassium permeabilities, however the asymmetric A waveform de-emphasizes depolarization and avoids AP generation. PNS threshold in terms of k-space coverage for this waveform is thus higher as compared with the symmetric waveform.
Figure 4 compares the transmembrane potential for subthreshold symmetric (solid curve) and asymmetric (dashed) waveforms. Due to the contribution of sodium channel activation that amplifies the effect of the depolarizing ramps, the symmetric waveform causes relatively strong depolarization and slightly weaker hyperpolarization, despite both ramps inducing the same E-field amplitude. On the other hand, the asymmetric waveform reduces depolarization and increases hyperpolarization of the nerve, thus reducing the overall PNS threshold.
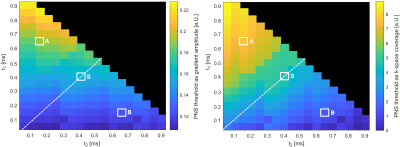
Figure 5 depicts PNS thresholds for combinations of t1 and t2 for a T= 1 ms trapezoid showing either the maximum gradient amplitude or maximum gradient area achieved without stimulation. Points on the diagonal (white dashed line) are symmetric waveforms. The cases highlighted with white markers correspond to three waveforms: A (t1 = 0.15 ms t2 = 0.65 ms), S (symmetric with t1 = t2 = 0.4 ms), and B (t1 = 0.65 ms t2 = 0.15 ms). Thus, S is the conventional symmetric trapezoid, and A and B are asymmetric but have identical flat-top time to S. A achieves a 38% higher PNS threshold compared to S, whereas B yields 41% lower thresholds.
Discussion
We investigate the impact of asymmetric readout gradient waveforms on nerve membrane dynamics for PNS reduction. We demonstrate that asymmetry can improve PNS thresholds while ensuring the same k-space coverage in the same time. We will validate this concept in realistic body models and realistic gradient coil geometries.Acknowledgements
NIH/NIGMS T32 GM008313
NIH NIBIB grant R01EB028250
Funding from Siemens Healthineers
References
[1] Tan et al., “Peripheral nerve stimulation limits of a high amplitude and slew rate magnetic field gradient coil for neuroimaging,” Magn Reson Med, vol. 83, no. 1, pp. 352–366, 2020.
[2] Weiger et al., “A high-performance gradient insert for rapid and short-T2 imaging at full duty cycle,” Magn Reson Med, vol. 79, no. 6, pp. 3256–3266, 2018.
[3] Wade et al., "Peripheral nerve stimulation thresholds of a high performance insertable head gradient coil." Proceedings of the 24th Annual Meeting of ISMRM, Singapore. 2016.
[4] Davids et al. “Predicting magnetostimulation thresholds in the peripheral nervous system using realistic body models,” Sci Rep, vol. 7, no. 1, p. 5316, 2017.
[5] Davids et al. "Optimization of MRI Gradient Coils with Explicit Peripheral Nerve Stimulation Constraints." IEEE Transactions on Medical Imaging (2020).
[6] Davids et al. "Prediction of peripheral nerve stimulation thresholds of MRI gradient coils using coupled electromagnetic and neurodynamic simulations." Magnetic resonance in medicine 81.1 (2019): 686-701.
[7] Davids M, Guérin B, Malzacher M, Schad LR, Wald LL. Predicting magnetostimulation thresholds in the peripheral nervous system using realistic body models. Sci Rep. 2017;7:5316.
[8] McIntyre et al., “Modeling the excitability of mammalian nerve fibers: Influence of afterpotentials on the recovery cycle”. J Neurophysiol. 87(2), 2002.
Figures
Figure 1: Example of symmetric and asymmetric waveforms. Every trapezoid is characterized by two rise times (t1, t2) and the full duration T. The plateau time is denoted by tp=T - t1 - t2, and G denotes the peak gradient amplitude. The symmetric waveform (top) uses the same rise times t1 = t2 whereas the asymmetric waveform uses different rise times (t1 > t2 in this case). A full trapezoidal pulse train is generated by concatenating multiple trapezoids with every odd numbered trapezoid having opposite polarity and interchanged rise times t1 and t2.
Figure 2: Left: Nerve segment with a single bend embedded in a homogeneous electric field produced by a hypothetical coil. The E-field induces a triangular electric potential along the nerve. Right: Nerve response given as transmembrane potential difference (relative to the resting potential) over the time course of an applied symmetric trapezoidal waveform (x-axis) for different locations along the nerve fiber (y-axis). Periods of alternating positive and negative slew cause depolarization (red) and hyperpolarization (green), until an AP is initiated after ~11.5 ms.
Figure 3: Nerve membrane responses in terms of transmembrane potential difference (2nd row) and sodium/potassium permeability (3rd row) for a symmetric and two asymmetric waveforms. All waveforms achieve the same k-space coverage. The symmetric waveform causes three APs. Using an asymmetric waveform (case A) with longer rise time t1 (up-ramp) and shorter rise time t2 (down-ramp) reduces the nerve’s depolarization and increases it’s hyperpolarization, thus suppressing AP formation. The asymmetric waveform case B has the opposite effect, inducing even more APs.
Figure 4: Examples of longer sub-threshold symmetric (solid lines, 1st row) and asymmetric gradient waveforms (dashed lines, 2nd row) and their corresponding nerve responses in terms of transmembrane potential as a function of time. The symmetric waveform induces a nerve response dominantly in the depolarized regime (i.e., closer to AP initiation), whereas the asymmetric waveform strongly shifts the nerve into the hyperpolarized state, thus reducing its propensity for AP formation.
Figure 5: PNS thresholds given as gradient amplitude (left) and corresponding k-space coverage (right) for the parameter space spanned by the independent rise times t1 (y-axis) and t2 (x-axis). Each square corresponds to a T = 1 ms period waveform. Waveforms along the diagonal (white-dashed line) correspond to symmetric waveforms, while all other waveforms are asymmetric. The asymmetric waveform (A) achieves a 38% increase of PNS threshold in terms of k-space coverage, compared to the symmetric waveform S. The threshold of the asymmetric waveform B is 41% lower than that of waveform S.