0400
Training Data Distribution Significantly Impacts the Estimation of Tissue Microstructure with Machine Learning1Centre for Medical Image Computing, University College London, London, United Kingdom, 2Great Ormond Street Institute of Child Health, University College London, London, United Kingdom
Synopsis
The performance of supervised machine learning tools is only as good as the data used to train them. In this work, we investigate the impact of training data distribution on tissue microstructure estimates in the human brain. We focus on two strategies: uniform sampling from the entire parameter space and sampling from parameter combinations observed using traditional model fitting. We demonstrate that training on previously observed combinations may be advantageous for detecting small variations in healthy tissue. However, for detecting atypical tissue abnormalities, our results favour uniform training data sampling in which all plausible parameter combinations are represented.
Introduction
The performance of supervised machine learning techniques relies on the quality and choice of data used for training. In the absence of balanced training data, artificial intelligence may learn disruptive racial1 and gender2 biases. In microstructure imaging, balancing training data to ensure that different parameter combinations are fairly represented is not trivial, as we do not have access to ground truth tissue microstructure. Recent works that leverage supervised machine learning for microstructural parameter estimation typically employ one of two training data distribution strategies: (1) uniform sampling from the entire plausible parameter space3-6 or (2) parameter combinations obtained from traditional model fitting7-10.In this work, we compare these two training data distribution strategies in microstructure imaging. To ensure that the complexity of the estimation task and the dimensionality of the parameter space are low, we use a simple two-compartment biophysical model that has two independent parameters11,12. Results from simulations and in-vivo human-brain data demonstrate that training data distribution indeed has a strong impact on the precision and accuracy of microstructure estimates. We show that training on in-vivo parameter combinations facilitates high accuracy and precision in typical parameter combinations seen in healthy tissue, whereas uniform training data distribution may be favourable for capturing atypical parameter combinations, such as in potential lesions.
Methods
Data AcquisitionSix healthy volunteers were scanned on a 3T Siemens Prisma scanner using a 64-channel head coil. We acquired diffusion weighted images with b-values of [1000, 2000, 3500, 5000] s/mm2 and a total of 128 uniformly distributed gradient directions13, as well as 12 images with no diffusion weighting. Measurement parameters include isotropic 2 mm resolution, TE = 94 ms and TR = 9.2 s. Additionally, a 3D T1-weighted MPRAGE with 1 mm isotropic resolution was acquired and segmented using FreeSurfer14.
Biophysical Model
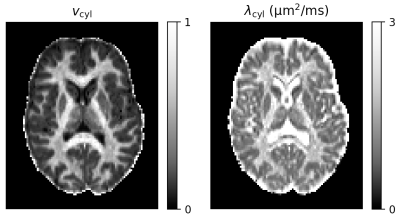
We fit diffusion data to the two-compartment SMT model11,12 in which brain tissue is assumed to consist of heterogeneously oriented cylindrical compartments and the surrounding extra-cellular volume. This model has two independent parameters: the volume fraction of cylindrical compartments (vcyl) and the diffusivity parallel to cylindrical compartments (λcyl).
Parameter Estimation
To estimate model parameters, we used two strategies: traditional model fitting (available at https://github.com/ekaden/smt) and supervised machine learning. For the machine learning strategy, we trained a number of artificial neural networks with the following shared properties:
- Three fully connected layers
- Mean square error loss criterion, stochastic gradient descent
- Trained on 219 synthetic data samples from the parameter space bounded by 0 ≤ vcyl ≤ 1 and 0 ≤ λcyl ≤ 3 μm2/ms.
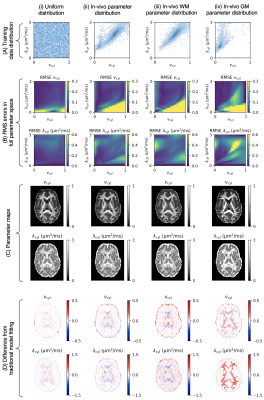
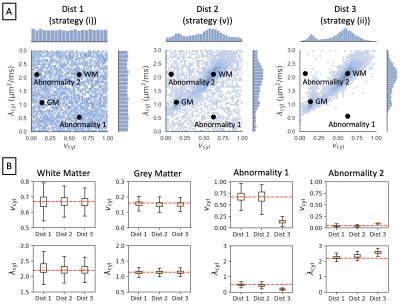
The only difference between each trained network was the distribution of the synthetic training data. We used the following distributions, visualised in Figure 2A and Figure 3A:
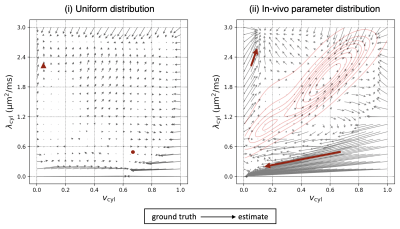
(i) uniform distribution
(ii) in-vivo parameter combinations from traditional model fitting in 5 subjects
(iii) subset of (ii) from white matter voxels
(iv) subset of (ii) from grey matter voxels
(v) half the samples drawn from (i) and half drawn from (ii)
Our primary focus is on comparing distributions (i) and (ii), as these are most commonly used in current literature. Distributions (iii) and (iv) serve to probe the estimation of healthy grey matter and white matter parameter combinations when these are not seen at training, whereas distribution (v) shows how estimation performance transitions between distribution (i) and (ii).
Results and Discussion
Figure 1 shows reference parameter maps for vcyl and λcyl estimated using traditional model fitting for a single subject. In Figure 2 we demonstrate that neural networks trained on different data distributions estimate different microstructural parameters, and that parameter combinations not represented in the training data tend to be estimated poorly. Of the tested neural networks, training data distributions (i) and (ii) provide similar maps to traditional model fitting.In Figure 3 we show that the in-vivo distribution (ii) estimates typical white matter and grey matter parameter combinations with higher precision and accuracy than uniform training data distribution (i). However, parameter combinations that are not typical in healthy human brain, marked as ‘Abnormality 1’ and ‘Abnormality 2’, are estimated poorly using in-vivo distribution (ii) compared to uniform distribution (i).
Finally, in Figure 4, we show how bias in estimates varies throughout the parameter space. The figure highlights parameter combinations that act as “sinks” in that estimates of other parameter combinations are biased towards these regions. For example, in the vicinity of densely sampled parameter combinations in the in-vivo distribution (ii), estimates appear to be biased towards the densest regions. However, “sinks” also appear in other regions of the parameter space, including regions that are not densely sampled in training.
Conclusion
We demonstrate that the distribution of training data has a significant impact on microstructural parameter estimates both in simulations and in-vivo in the human brain. Our findings suggest that a uniform training data distribution approach is favourable for estimating abnormal parameter combinations, e.g. in lesions or other pathologies. However, when the task is to detect small changes in tissue parameters, it may be favourable to weight training data according to a priori information on the expected parameter combinations. Future work might investigate finding the optimal training data distribution for a given estimation task.Acknowledgements
NGG thanks the London Interdisciplinary Bioscience PhD Consortium and is funded by BBSRC grant BB/M009513/1. MP is supported by UKRI Future Leaders Fellowship (MR/T020296/1). We also thank EPSRC platform grant EP/M020533/1, the NIHR UCLH Biomedical Research Centre and the NIHR GOSH Biomedical Research Centre for funding. We acknowledge Enrico Kaden’s background contributions to funding acquisition that supported this work, conceptualisation, design and set-up of the diffusion experiment, conceptualisation of the deep-learning model fitting framework for which similar ideas are used in our code, initial discussions on studying the effects of training data distribution. We also thank Filip Szczepankiewicz and Markus Nilsson for sharing their diffusion EPI sequence.References
[1] Obermeyer, Z., B. Powers, C. Vogeli, S. Mullainathan (2019). “Dissecting racial bias in an algorithm used to manage health of populations”. In: Science 366.6464, pp. 447-453.
[2] Cirillo, D., S. Catuara-Solarz, C. Morey, E. Guney, L. Subirats, S. Mellino, A. Gigante, A. Valencia, M. J. Rementeria, A. S. Chadha, and N. Mavridis (2020). “Sex and gender differences and biases in artificial intelligence for biomedicine and healthcare”. In: npj Digital Medicine 3, pp. 81.
[3] Nedjati-Gilani, G. L., T. Schneider, M. C. Hall, N. Cawley, I. Hill, O. Ciccarelli, I. Drobnjak, C. A. M. Gandini Wheeler-Kingshott, and D. C. Alexander (2017). “Machine learning based compartment models with permeability for white matter microstructure imaging”. In: Neuroimage 150, pp. 119–135.
[4] Palombo, M., A. Ianus, D. Nunes, M. Guerreri, D. Nunes, D. C. Alexander, N. Shemesh, and H. Zhang (2020). “SANDI: a compartment-based model for non-invasive apparent soma and neurite imaging by diffusion MRI”. In: Neuroimage 15, p. 116835.
[5] Hill, I., M. Palombo, M. Santin, F. Branzoli, A. Philippe, D. Wassermann, M. Aigrot, B. Stankoff, A. B. Evencooren, M. Felfli, D. Langui, H. Zhang, S. Lehericy, A. Petiet, D. C. Alexander, O. Cicarelli, and I. Drobnjak (2020). “Machine learning based white matter models with permeability: An experimental study in cuprizone treated in-vivo mouse model of axonal demyelination”. In: Neuroimage 225, p. 117425.
[6] Gyori, N. G., C. A. Clark, I. Dragonu, D. C. Alexander, and E. Kaden (2019a). “In-vivo neural soma imaging using B-tensor encoding and deep learning”. In: In Proceedings of the ISMRM, p. 0059.
[7] Golkov, V., A. Dosovitskiy, J. I. Sperl, M. I. Menzel, M. Czisch, P. Samann, T. Brox, and D. Cremers (2016). “q-Space deep learning: twelve-fold shorter and model-free diffusion MRI scans”. In: IEEE Transactions on Medical Imaging 35.5, pp. 1344–1351.
[8] Koppers, S. and D. Merhof (2016). “Direct estimation of fibre orientations using deep learning in diffusion imaging”. In: International Workshop on Machine Learning in Medical Imaging, pp. 53-60.
[9] Aliotta, E., H. Nourzadeh, S. H. Patel (2020). “Extracting diffusion tensor fractional anisotropy and mean diffusivity from 3-direction DWI scans using deep learning”. In: Magnetic Resonance in Medicine 85.2, pp. 845-854.
[10] Chen, G., Y. Hong, Y. Zhang, J. Kim, K.M. Huynh, J. Ma, W. Lin, D. Shen, P. Yap (2020). “Estimating tissue microstructure with undersampled diffusion data via graph convolutional neural networks”. In: Medical Image Computing and Computer Assisted Intervention – MICCAI 2020, pp. 280-290.
[11] Kaden, E., F. Kruggel, and D. C. Alexander (2016a). “Quantitative mapping of the per-Axon diffusion coefficients in brain white matter”. In: Magnetic Resonance in1016 Medicine 75.4, pp. 1752–1763.
[12] Kaden, E., N. D. Kelm, R. P. Carson, M. D. Does, and D. C. Alexander (2016). “Multi-compartment microscopic diffusion imaging”. In: Neuroimage 139, pp. 346–359.
[13] Caruyer, E., C. Lenglet, G. Sapiro, and R. Deriche (2013). “Design of multishell sampling schemes with uniform coverage in diffusion MRI”. In: Magnetic Resonance in Medicine 69.6, pp. 1534–1540.
[14] Fischl, B. (2012). “FreeSurfer”. In: Neuroimage 62.2, pp. 774–781.
Figures