0399
Improved unsupervised physics-informed deep learning for intravoxel-incoherent motion modeling1Department of Radiology and Nuclear Medicine, Amsterdam UMC, Amsterdam, Netherlands, 2Department of Radiology and Nuclear Medicine, St. Olav's University Hospital, Trondheim, Norway, 3Department of Circulation and Medical Imaging, NTNU: Norwegian University of Science and Technology, Trondheim, Norway, 4Centre for Big Data Research in Health, UNSW, Sydney, Australia, 5Department of Medical Oncology, Amsterdam UMC, Amsterdam, Netherlands, 6Department of Radiation Oncology, Amsterdam UMC, Amsterdam, Netherlands
Synopsis
We implemented an improved unsupervised physics-informed deep neural network approach for intravoxel-incoherent motion modeling to DWI data by exploring several hyperparameters. Whereas the original IVIM-NETorig showed high dependency between the predicted IVIM parameters, our optimized approach resolved this high dependency, produced better accuracy and was more consistent. In simulations, IVIM-NEToptim outperformed least-squares and Bayesian fitting approaches. In patients with pancreatic ductal adenocarcinoma, IVIM-NEToptim produced substantially less noisy parameter maps and lower intersession within-subject standard deviations than the alternatives. IVIM-NEToptim also detected the most individual patients with significant parameter changes in the group of patients who received chemoradiotherapy.
Introduction
The intravoxel incoherent motion (IVIM) model1 for diffusion-weighted imaging (DWI) has shown promising results in studies for estimating predictive and prognostic cancer imaging biomarkers2–5, by estimating diffusion (D); capillary microcirculation (D*) and the perfusion fraction (f) simultaneously. However, despite its potential, it is not routinely used as a decision-making tool, partially because it renders noisy parameter maps and poor test-retest repeatability. Currently, Bayesian algorithms for IVIM fitting to DWI6 have been the most promising at producing smoother, less noisy parameter maps and outperforming the conventional least-squares approach (LS)7–9. Conversely, Bayesian approaches are substantially slower than the already slow LS approach10 and can lead to biased perfusion estimates11. Recently, we introduced a novel approach for IVIM fitting, using unsupervised physics-informed deep neural networks (PI-DNNs): IVIM-NETorig10, which greatly increased speed and performance. However, that proof-of-principle IVIM-NET study did not explore many hyperparameters and focused on volunteer data.Therefore, we improved IVIM-NET by exploring the architecture of the network, its training features and other hyperparameters in simulations. Furthermore, we explored the performance of our optimized 'IVIM-NEToptim' in patients with pancreatic ductal adenocarcinoma (PDAC) receiving neoadjuvant chemoradiotherapy (CRT).
Methods
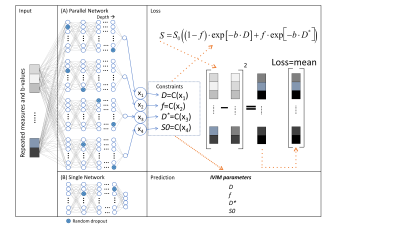
First, we implemented the original unsupervised PI-DNN, IVIM-NETorig, in Python 3.8 using PyTorch 0.4.112. The input layer consisted of neurons that took the normalized DWI signal. This was fed forward to 3 fully connected hidden layers and ended with the three IVIM parameters. To enforce the output layer to predict these IVIM parameters, a physics-based loss function was introduced that computed the mean-squared error between the input signal and the predicted IVIM signal.Next, seven novel hyperparameters were considiered in the PI-DNN (Figure 1) (fit S0, constraints, network architecture, number of hidden layers, dropout13, batch normalization14 and learning rate). For example, we implemented an alternative network architecture in which parameter values were predicted by independent sub-networks (parallel network architecture).
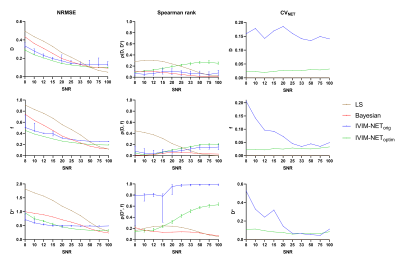
100,000 IVIM curves were simulated using: 0.5×10-3<D<3×10-3 mm2/s, 5<f<40%, and 10×10-3<D*<100×10-3 mm2/s, which are slightly broader than typical ranges found in abdominal IVIM15. The accuracy, independence, and consistency of IVIM-NET were evaluated for combinations of the hyperparameters by calculating the normalized root-mean-square error (NRMSE), Spearman’s ρ, and the coefficient of variation (CVNET), respectively. Because training a DNN is a stochastic process, each network variant was trained 50 times on identical data, hence CVNET. The best performing network, IVIM-NEToptim, was compared to a LS16,17 and a Bayesian approach (used in previous work10) at different SNRs ranging from 8 to 100.
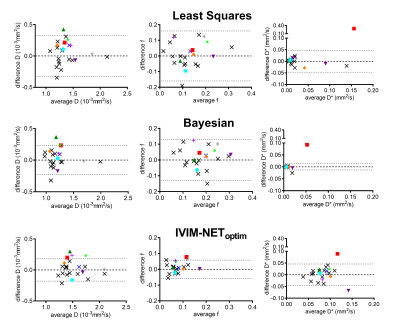
IVIM-NEToptim’s performance was then evaluated in twenty-three PDAC patients who underwent IVIM imaging. Fourteen received no treatment between two repeated scan sessions and nine received CRT between the repeated sessions. Bland-Altman plots (BAP) were plotted for patients from both cohorts. From the patients with repeated scans at baseline, intersession within-subject standard deviations (wSD) and 95% confidence intervals (95CI) were calculated, and were added to the BAP. If a patient from the treated cohort exceeded the 95CI, they were considered to have significant changes in tumor microstructure18. Furthermore, a paired t-test was performed in the treated cohort to test for significant parameter changes due to treatment for the whole cohort.
Results
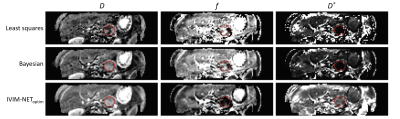
In simulations, although IVIM-NETorig showed substantially lower NRMSE for all estimated parameters than the LS and Bayesian approaches (8<SNR<50), it showed strong correlations between D* and f (high ρ(D*,f); Figure 2) and considerable CVNET (Figure 2). IVIM-NEToptim resolved this high dependency and substantially reduced the NRMSE and CVNET, making it superior to the LS and Bayesian approaches (8<SNR<50) (Figure 2). IVIM-NEToptim consisted of a parallel network architecture with 4 hidden layers, batch normalization, dropout of 10%, sigmoid constraints and fitted S0. Optimized training was performed using an Adam optimizer with a learning rate of 1×10-4.In vivo, IVIM-NEToptim showed less noisy and more detailed parameter maps (Figure 3), with lower wSD for D and f than the LS and Bayesian approaches (Table 1). In the treated cohort IVIM-NEToptim found a significant 52% increase in mean f after treatment, whereas the LS approach found a significant 12% increase in D after treatment (Table 1). For IVIM-NEToptim the p-value for D was 0.07 with an increase of 7%. Figure 4 shows that IVIM-NEToptim detected the most individual patients with significant parameter changes (n=7) after CRT, compared to the LS (n=2) and Bayesian approaches (n=4).
Discussion
We successfully developed and trained IVIM-NEToptim, an unsupervised PI-DNN IVIM fitting approach to DWI. In simulations, IVIM-NEToptim outperformed the original version, IVIM-NETorig, by offering more accurate, independent, and consistent estimates of D, f and D*. Furthermore, simulations showed that IVIM-NEToptim had substantially better accuracy than the LS and Bayesian approaches. In vivo, IVIM-NEToptim showed the most detailed and least noisy parameter maps, and was the only estimator to find a significant change in the perfusion fraction for the whole cohort receiving CRT. Furthermore, IVIM-NEToptim was associated with the best test-retest repeatability (smallest wSD) for D and f, which allowed it to detect the most individual patients with significant changes after CRT.Conclusion
IVIM-NEToptim outperforms state-of-the-art fitting approaches as it computes more detailed parameter maps, offers better test-retest repeatability for D and f and detects the most individual patients with significant parameter changes throughout CRT for all IVIM parameters.Acknowledgements
Misha P. T. Kaandorp and Peter T. While gratefully acknowledge support from the Research Council of Norway under FRIPRO Researcher Project 302624.References
1. Le Bihan D, Breton E, Lallemand D, Aubin M, Vignaud J LM. Separation of diffusion and perfusion in intravoxel inco-herent motion MR imaging. Radiology. 1988;168:497–505.
2. Cho GY, Gennaro L, Sutton EJ, et al. Intravoxel incoherent motion (IVIM) histogram biomarkers for prediction of neoadjuvant treatment response in breast cancer patients. Eur J Radiol Open. 2017;4(August):101-107. doi:10.1016/j.ejro.2017.07.002
3. Zhu L, Wang H, Zhu L, et al. Predictive and prognostic value of intravoxel incoherent motion (IVIM) MR imaging in patients with advanced cervical cancers undergoing concurrent chemo-radiotherapy. Sci Rep. 2017;7(1):1-9. doi:10.1038/s41598-017-11988-2
4. Ma W, Zhang G, Ren J, et al. Quantitative parameters of intravoxel incoherent motion diffusion weighted imaging (IVIM-DWI): potential application in predicting pathological grades of pancreatic ductal adenocarcinoma. Quant Imaging Med Surg. 2018;8(3):301-310. doi:10.21037/qims.2018.04.08
5. Klaassen R, Steins A, Gurney-Champion OJ, et al. Pathological validation and prognostic potential of quantitative MRI in the characterization of pancreas cancer: preliminary experience. Mol Oncol. 2020;14(9):2176-2189. doi:10.1002/1878-0261.12688
6. Neil JJ, Bretthorst GL. On the use of bayesian probability theory for analysis of exponential decay date: An example taken from intravoxel incoherent motion experiments. Magn Reson Med. 1993;29(5):642-647. doi:10.1002/mrm.1910290510
7. Gurney-Champion OJ, Klaassen R, Froeling M, et al. Comparison of six fit algorithms for the intravoxel incoherent motion model of diffusion-weighted magnetic resonance imaging data of pancreatic cancer patients. PLoS One. 2018;13(4):1-18. doi:10.1371/journal.pone.0194590
8. Orton MR, Collins DJ, Koh DM, Leach MO. Improved intravoxel incoherent motion analysis of diffusion weighted imaging by data driven Bayesian modeling. Magn Reson Med. 2014;71(1):411-420. doi:10.1002/mrm.24649
9. Barbieri S, Donati OF, Froehlich JM, Thoeny HC. Impact of the calculation algorithm on biexponential fitting of diffusion-weighted MRI in upper abdominal organs. Magn Reson Med. 2016;75(5):2175-2184. doi:10.1002/mrm.25765
10. Barbieri S, Gurney-Champion OJ, Klaassen R, Thoeny HC. Deep learning how to fit an intravoxel incoherent motion model to diffusion-weighted MRI. Magn Reson Med. 2020;83(1):312-321. doi:10.1002/mrm.27910
11. While PT. A comparative simulation study of bayesian fitting approaches to intravoxel incoherent motion modeling in diffusion-weighted MRI. Magn Reson Med. 2017;78(6):2373-2387. doi:10.1002/mrm.26598
12. Paszke A, Gross S, Chintala S, et al. Automatic differentiation in PyTorch. NIPS-W. 2017;22(1):2-8. doi:10.1145/24680.24681
13. Srivastava N, Hinton G, Krizhevsky A, Sutskever I, Salakhutdinov R. Dropout: A simple way to prevent neural networks from overfitting. J Mach Learn Res. 2014;15:1929-1958.
14. Ioffe S, Szegedy C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. 32nd Int Conf Mach Learn ICML 2015. 2015;1:448-456.
15. Barbieri S, Donati OF, Froehlich JM, Thoeny HC. Comparison of intravoxel incoherent motion parameters across MR imagers and field strengths: Evaluation in upper abdominal organs. Radiology. 2016;279(3):784-794. doi:10.1148/radiol.2015151244
16. K. Levenberg. A method for the solution of certain non-linear problems in Least squares. Q Appl Math. 1944;2(2):164-168. doi:10.1177/002205741408001401
17. Marquardt DW. An algorithm for least-squares estimation of nonlinear parameters. J Soc Ind Appl Math. 1963;11(2):431-441.
18. Bland JM, Altman DG. Statistics Notes: Measurement error. Bmj. 1996;313(7059):744-744. doi:10.1136/bmj.313.7059.744
Figures