0398
Gradient waveform design for cross-term-compensated diffusion MRI: Demonstration of tensor-valued encoding in phantom and simulations
Filip Szczepankiewicz1 and Jens Sjölund2
1Clinical Sciences Lund, Lund University, Lund, Sweden, 2Department of Information Technology, Uppsala University, Uppsala, Sweden
1Clinical Sciences Lund, Lund University, Lund, Sweden, 2Department of Information Technology, Uppsala University, Uppsala, Sweden
Synopsis
Diffusion weighted imaging is perturbed by the presence of background gradients, or so-called 'cross-terms,' causing bias in estimated parameters and fiber orientations. In this work, we present a novel gradient waveform design that removes the cross-term sensitivity entirely. This design is valuable for diffusion MRI methods that are otherwise corrupted by background gradients, and it also facilitates arbitrary sequence timing, b-tensor shapes and suppression of concomitant gradient effects.
Introduction
Diffusion MRI relies on a careful application of magnetic field gradients to sensitize the signal to the motion of spin. However, additional field gradients are caused by heterogeneous magnetic susceptibility (e.g. air/tissue interfaces) or by poor shimming$$$~$$$[1]. These 'background gradients' interact with the desired gradient waveform, creating so-called 'cross-terms,' which cause unwanted spin dephasing and bias in the estimated parameters$$$~$$$[2]. Finsterbusch$$$~$$$[3] has proposed an elegant sequence design for cross-term compensation, however, it requires stimulated spin-echos and considers only diffusion encoding along a single direction per acquisition.$$$~~~~~~$$$In this work, we propose a general and versatile framework for generating optimized gradient waveforms that suppress effects of stationary background gradients by constraining the 'cross-term sensitivity' in numerical optimization. We validate the novel gradient waveform design in simulations and phantom experiments, and show that they are vastly more accurate in the presence of background gradients compared to non-compensated waveforms. Thereby our approach facilitates accurate diffusion MRI in materials or regions plagued by background gradients.
Theory
In the presence of a time-stationary background gradient, the actual gradient waveform $$$(\mathbf{g}_\mathrm{a})$$$ is the sum of the desired $$$(\mathbf{g}_\mathrm{d})$$$ and the background $$$(\mathbf{g}_\mathrm{b})$$$ waveforms$$\mathbf{g}_\mathrm{a}(t)=\mathbf{g}_\mathrm{d}(t)+\mathbf{g}_\mathrm{b}(t)=\mathbf{g}_\mathrm{d}(t)+\mathbf{g}_\mathrm{b}h(t)$$
where $$$\mathbf{g}_\mathrm{b}(t)$$$ is expressed as a stationary vector, $$$\mathbf{g}_\mathrm{b}$$$, and a sign function, $$$h(t)$$$, that tracks the spin dephasing direction. The impact of cross-terms caused by $$$\mathbf{g}_\mathrm{b}$$$ can be mitigated by designing $$$\mathbf{g}_\mathrm{d}$$$ to have a dephasing q-vector $$$\mathbf{q}(t)=\gamma\int_0^{t}\mathbf{g}(t')\mathrm{d}t'$$$ orthogonal to the q-vector caused by the background$$$~$$$[1], such that
$$\int_0^{\tau}\mathbf{q}_\mathrm{d}(t)\odot\mathbf{q}_\mathrm{b}(t)\mathrm{d}t=0$$
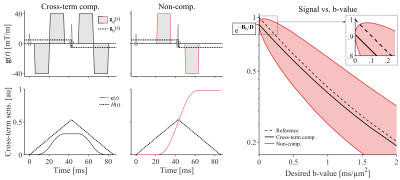
where '$$$\odot$$$' is element-wise multiplication, and $$$\tau$$$ is the echo time. Fig.1 shows waveforms with/without cross-term-compensation, and their effect on diffusion-weighted signal. As proposed in ref.$$$~$$$[4], cross-term-compensation can be achieved for arbitrary stationary background gradients and sequence timing by constraining the magnitude of the 'cross-term-sensitivity'
$$\mathbf{c}=\int_{0}^{\tau}\mathbf{q}_\mathrm{d}(t)H(t)\mathrm{d}t,$$
where $$$H(t)=\int_0^{\tau}h(t')\mathrm{d}t'$$$ is a triangular function centered on $$$\tau/2$$$.
Methods
Waveform optimization - Gradient waveforms were cross-term-compensated by introducing a linear equality constraint on the cross-term-sensitivity in the numerical optimization framework by Sjölund et al.$$$~$$$[5], such that $$$\mathbf{c}=0.$$$ Variants that yield linear, planar and spherical b-tensors were generated with gradient amplitude $$$<80$$$ mT/m, slew rate $$$<100$$$ T/m/s$$$~$$$[5] and included suppression of concomitant gradient effects$$$~$$$[6].$$$~$$$
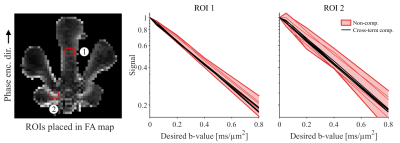
Phantom experiments - A water-filled plastic bottle with a folded base was used to provoke local field gradients. We used a 3T-Prisma system (Siemens Healthcare, Germany) and a custom spin-echo EPI pulse sequence that enables user-defined gradient waveforms$$$~$$$[7]. Waveforms with and without cross-term-compensation were executed with identical imaging parameters: TR$$$~=~3~$$$s, TE$$$~=~125~$$$ms, no partial-Fourier, 2 mm isotropic voxels, FOV$$$~=220\times220~$$$mm$$$^2$$$, $$$b=[0.0,~0.05,~0.10,~0.20,~0.40,~0.80]~{\mathrm{ms/µm^2}}$$$ (six rotations each), and 'advanced' shimming. Fractional anisotropy (FA) from diffusion tensor imaging$$$~$$$[8] was used as a proxy for the rotation variance of signal, i.e., high FA indicates large influence from background gradients. All ROIs were manually placed away from the water/air interface to avoid confounding effects from eddy currents.
$$$~$$$
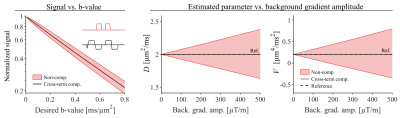
Simulations of signal and parameter error - Signal was simulated under the same conditions as the phantom experiments. Background gradients were simulated by adding a stationary offset to $$$\mathbf{g}_\mathrm{d}(t)$$$ along 100 directions with magnitudes between 0-500 µT/m. Signal was generated along each direction separately using the actual b-value $$$(b_\mathrm{a})$$$, such that
$$S(b_\mathrm{a})=S_0\,\mathrm{exp}(-b_\mathrm{a}D+1/2b_\mathrm{a}^2V)$$
where the true diffusivity and diffusional variance were, $$$D=2~\mathrm{µm^2/ms}$$$ and $$$V=0.2~\mathrm{µm^4/ms^2}$$$. The parameter estimation used the same signal representation, but employed the desired b-values $$$(b_\mathrm{d}$$$ instead of $$$b_\mathrm{a})$$$ in the fitting to provoke the estimation bias.
Results
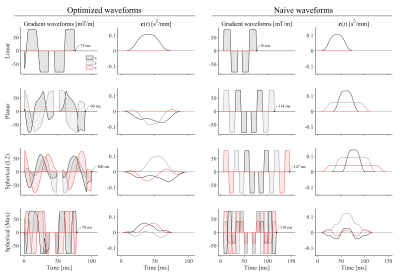
Fig.2 shows examples of cross-term-compensated gradient waveforms optimized by the proposed design along with a simple but less efficient design$$$~$$$[4]. All examples yield $$$b=2~\mathrm{ms/µm^2}$$$ and optimized waveforms can reduce encoding time by up to 50 ms.Fig.3 showcases that background gradients can have a large impact on quantification, and that cross-term compensation yields vastly more accurate signal.
Fig.4 provides a closer look at signal vs. $$$b$$$, and shows that the proposed cross-term compensation is robust in regions with and without suspected eddy current influence.
Fig.5 shows that significant parameter errors can be caused by background gradients, but that the compensated waveforms are robust to such effects. Even if the signal is reduced somewhat by the background (Fig.1), the normalized signal, $$$S(b)/S_0$$$, remains accurate.
Discussion and conclusions
We have presented a gradient waveform design that successfully removes the influence of background gradient cross-terms. Our design therefore enables accurate diffusion measurements even in the presence of stationary background gradients regardless of their direction and magnitude. This is valuable when imaging close to tissue/air interfaces, e.g. ear-canal, sinuses, implants etc, and is especially critical for methods that rely on accurate measurements at low b-values, such as IVIM.$$$~~~~~~$$$Our framework is highly versatile; waveforms can be tailored to specific MRI hardware, arbitrary sequence timing and b-tensor shapes$$$~$$$[5] and includes compensation for concomitant gradient$$$~$$$[6] and motion$$$~$$$[9]. Unlike previous methods$$$~$$$[3,10], it is compatible with spin-echo sequences with one (or more) refocusing pulse which are expected to yield shorter echo-times and SNR, and our design does not require geometric averaging over antipodal measurements$$$~$$$[11].
$$$~~~~~~$$$We note that the inclusion of cross-term-compensation reduces the encoding efficiency, warranting consideration of its use in cases where careful shimming may be sufficient. Furthermore, the generated waveforms tend to have more encoding power at shorter diffusion times, which may introduce confounding effects$$$~$$$[4]. The optimization code will be shared in open source after publication$$$~$$$[12].
Acknowledgements
This work was supported by grants from Swedish Research Council (2016-03443). We thank Siemens Healthcare (Erlangen, Germany) for access to the pulse sequence programming environment.References
[1] Novikov, Reisert, and Kiselev, “Effects of mesoscopic susceptibil-ity and transverse relaxation on diffusion NMR” J Magn. Reson., 2018.
[2] Lian, Williams, and Lowe, “Magnetic resonance imaging of diffusion in thepresence of background gradients and imaging of background gradients” JMR, 1994.
[3] Finsterbusch, “Cross-term-compensated pulsed-gradient stimulated echoMR with asymmetric gradient pulse lengths” J Magn Reson, 2008.
[4] Szczepankiewicz, Westin, and Nilsson, “Gradient waveformdesign for tensor-valued encoding in diffusion MRI” J Neuroscience Meth,2020.
[5] Sjölund et al., “Constrained optimization of gradient waveforms forgeneralized diffusion encoding” JMR, 2015.
[6] Szczepankiewicz, Westin, and Nilsson, “Maxwell-compensateddesign of asymmetric gradient waveforms for tensor-valued diffusion encod-ing” MRM, 2019.
[7] Szczepankiewicz et al., “Tensor-valued diffusion encoding for diffusional variance decomposition(DIVIDE): Technical feasibility in clinical MRI systems” PLoSOne, 2019.
[8] Basser, Mattiello, and LeBihan, “MR diffusion tensor spectroscopyand imaging” BiophysJ, 1994.
[9] Szczepankiewicz et al., “Motion-compensated gradient waveformsfor tensor-valued diffusion encoding by constrained numerical optimiza-tion” MRM, 2020.
[10] Valette et al., “A new sequence for single-shot diffusion-weightedNMR spectroscopy by the trace of the diffusion tensor” MRM, 2012.
[11] Neeman, Freyer, and Sillerud, “A simple method for obtaining cross-term-free images for diffusion anisotropy studies in NMR microimaging” MRM,1991.
[12] Numerical optimization of gradient waveforms for tensor-valued dMRI (https://github.com/jsjol/now). GitHub, 2015.
Figures
Figure 1 - Cross-terms depend on the gradient waveform, and their impact can be minimized by cross-term compensation. Here, an exaggerated 5 mT/m-background gradient is applied to visualize the impact on the diffusion-weighted signal. Compensated waveforms (black line) have a more accurate S(b)/S0, whereas non-compensated waveforms can over and underestimate the signal (red interval), even increasing signal with b-value (inset plot)! Both variants are attenuated by the background diffusion-weighting, exp(-Bb:D).
Figure 2 - Optimized cross-term-compensated gradient waveforms are more efficient than naive counterparts (mirror symmetric bipolar [4]). All waveforms yield b = 2 ms/µm2 under the same constraints on amplitude and slew-rate. The proposed design is more efficient and can reduce encoding time by 20-50 ms for planar and spherical encoding. Note that the available time for encoding is 6 ms longer before the refocusing pulse, compared to after. As desired, optimized sensitivity trajectories terminate at c = 0, indicating robustness to cross-terms.
Figure 3 - A water phantom with a folded surface demonstrates the effect of stationary background gradients. In addition to image distortions, background gradients cause signal variation when waveforms are rotated, causing a positive bias in FA (true value is zero in pure water). Direction encoded color-maps, brightness scaled by FA$$$\in[0.0~0.4]$$$, show prominent coross-term effects for conventional waveforms (high FA), compared to cross-term compensated waveforms, which appear more robust to background gradients (low FA). Violin plots show FA distributions in the slice.
Figure 4 - Signal vs. b-curves in the water phantom show that non-compensated waveforms suffer a significant directional dependency (each red line shows a rotation of the waveform and the red surface shows the observed interval). By contrast, cross-term-compensated waveforms are invariant to rotation (black lines show tight grouping). Regions 1 and 2 are placed away from/close to a surface, to represent locations where eddy-currents may be less/more impactful. Regardless of position, cross-term compensated waveforms are vastly more robust.
Figure 5 - Simulations of realistic background gradient magnitudes 0-500 µT/m show that signal, diffusivity (D) and diffusional variance (V) can be markedly under and over-estimated if waveforms are not cross-term compensated (red intervals show possible values). In all cases, cross-term-compensated waveforms yielded accurate signal decay (S(b)/S0) and parameter estimation, regardless of the background gradient. Inset plots show the actual gradient waveforms used in phantom measurements and simulations; planar and spherical waveforms gave similar results (not shown).