Introduction

Modern MRI methods often rely on acceleration methods including Parallel MRI (PMRI) and compressive sensing to reduce the scan time. Calibrated methods such as SENSE/GRAPPA [1, 2] as well as calibrationless structured low-rank methods [3, 4] have been introduced to recover the images from undersampled measurements. Our recent work has shown that linear relations between their k-space measurements can be capitalized using k-space deep-learning (DL) strategies [5],which are more computationally efficient than classical methods. Despite the great progress made in image reconstruction, undersampling artifacts and blurring of image edges are inevitable at high acceleration factors; these artifacts can deteriorate the performance of segmentation algorithms that exploit the edges and the coherence of image intensities within regions that would be impacted by undersampling.
We introduce a novel framework for DL based calibration-free MRI reconstruction and segmentation. The contributions include a novel image domain deep structured low-rank framework for calibration-free PMRI recovery and a joint segmentation-reconstruction framework to minimize segmentation errors introduced by undersampling artifacts and improve reconstruction quality.

Proposed Method

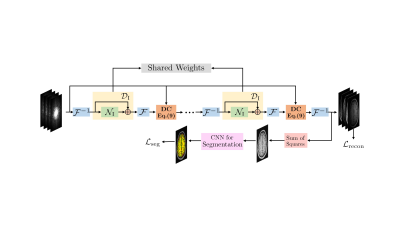
The forward model is defined as, \begin{equation} \mathbf b_i = \underbrace{\mathcal S \mathcal F}_{\mathcal A} ~\gamma_i + \mathbf n_i, \hspace{2pt} i = 1 \ldots N \end{equation} where $$$\mathbf b_i$$$ are noisy Fourier coefficients of $$$i^{th}$$$ coil image $$$\gamma_i$$$ corrupted by Gaussian noise $$$\mathbf n_i$$$, $$$N$$$ is the total number of coils, $$$\mathcal F$$$ is the Fourier operator and $$$\mathcal S$$$ denotes the sampling operator. According to the CLEAR formulation [6], if $$$P_{\mathbf s_0}$$$ is a patch extraction operator that extracts $$$M\times M$$$ patches of $$$\gamma_i(\mathbf s)$$$ centered at $$$\mathbf s_0$$$, the matrices \begin{equation}\label{key} \boldsymbol\Gamma_{\mathbf s} = \begin{bmatrix} P_{\mathbf s}(\gamma_1)| & \ldots & |P_{\mathbf s}(\gamma_N) \end{bmatrix} \end{equation} are low-rank. It solves for $$$\Gamma = \begin{bmatrix} \gamma_1,.. ,\gamma_N \end{bmatrix}$$$ as the nuclear norm minimization problem \begin{equation}\label{clear} \boldsymbol \Gamma = \arg \min_{\boldsymbol \Gamma} \|\mathcal A(\boldsymbol\Gamma)-\mathbf B\|^2 + \lambda\sum_s \|\boldsymbol\Gamma_{\mathbf s}\|_* \end{equation}.
Using the iterative reweighted least squares formulation, we obtain a model-based DL network alternating between \begin{eqnarray} \mathbf X_{n} &=& \mathcal D_{\rm I}(\boldsymbol \Gamma_n)\\ \widehat{\boldsymbol \Gamma}_{n+1} &=& (\mathcal A^H \mathcal A + \lambda \mathbf I)^{-1}(\mathcal A^H \mathbf B + \lambda \widehat{\mathbf X}_{n}) \end{eqnarray}

Similar to [5], the network is unrolled and trained end-to-end with exemplar data with CNN weights shared across iterations. The training loss is $$$\mathcal L_{\rm recon} = \|\boldsymbol \Gamma - \boldsymbol \Gamma_{gs} \|^2$$$ , where $$$\boldsymbol\Gamma$$$ is the prediction and $$$\boldsymbol \Gamma_{gs}$$$ is the gold standard multicoil data obtained from fully sampled measurements. The proposed method I-DSLR eliminates the need for calibration data for estimating the coil sensitivities or linear filters $$$\mathbf Q_s$$$.

We propose a multi-task deep network as shown in Fig .1, trained end-to-end. A segmentation network is attached to the final iteration of the I-DSLR. We use a weighted linear combination of normalized mean squared error $$$\mathcal L_{\rm recon}$$$ and pixel-wise multi-label cross entropy $$$\mathcal L_{\rm seg} = -\sum_p \boldsymbol{\phi}_{p}^{gs} \ln \boldsymbol{\phi}_{p}$$$ error for training. \begin{equation} \mathcal L_{\rm total} = \mathcal L_{\rm recon} + \beta \mathcal L_{\rm seg} \end{equation} For each pixel $$$p$$$, $$$\boldsymbol{\phi}_{gs}$$$ is the gold standard segmentation on the sum-of-squares image obtained from $$$\boldsymbol{\Gamma}_{gs}$$$ and $$$\boldsymbol{\phi}$$$ is the segmentation CNN output.

Experiments and Results

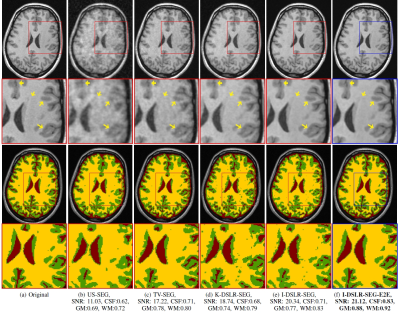
We perform experiments on the publicly available Calgary Campinas Dataset (CCP) [7]. It consists of 12-channel raw k-space data of T1-weighted brain MRI scans from a Discovery MR750 3T scanner for 67 subjects. The slice dimensions are 208 x 170 for axial view of the brain. Ground truth segmentations for the slices were generated using the FAST software. Forty subjects (40 x 256 = 10240 slices) were used for training, 7 for validation and the remaining 20 for testing purposes. 2D non-uniform cartesian variable density undersampling masks with different acceleration factors were used for experiments; readout direction is orthogonal to axial slices.
A pre-trained I-DSLR network cascaded with a segmentation network pre-trained using fully sampled data (I-DSLR-SEG) is compared against k-space Deep-SLR method(K-DSLR-SEG), total variation (TV-SEG) and undersampled (US-SEG) in the same setting. We also compare against I-DSLR-SEG-E2E, a cascade of IDSLR and UNET segmentation networks trained end-to-end (E2E). In TV-SEG, the segmentation network is trained and tested on images reconstructed using TV. Similarly, for US-SEG, the segmentation network is trained and tested on undersampled datasets.
A comparison of the methods is shown in Fig. 2. I-DSLR has sharper edges compared to US, TV and K-DSLR. The corresponding segmentation performance improves with increase in reconstruction quality. The end-to-end training strategy in I-DSLRSEG-E2E further improves quality over I-DSLR-SEG. Its improved reconstruction can be attributed to the regularization by the segmentation network and vice-versa.

Conclusion

We introduced a novel image domain model-based DL approach for calibrationless PMRI recovery. It is a non-linear extension of locally low rank methods for calibrationless parallel MRI. The experiments show that additional annihilation relations exploited by I-DSLR approach offers better performance over k-space approach K-DSLR [5]. We introduce a multi-task framework where I-DSLR is cascaded with a segmentation dedicated DL network which is trained end-to-end. The networks regularize each other, thereby reducing the errors caused from undersampling artifacts. Experiments show that the segmentation accuracy depends on the reconstruction quality. I-DSLR-SEG-E2E reduces the errors propagating to segmentation network, thus outperforming methods that cascade independently trained networks.

Acknowledgements

This work is supported by NIH 1R01EB019961-01A1.