0392
Learning-based non-linear registration robust to MRI-sequence contrast1Department of Radiology, Harvard Medical School, Boston, MA, United States, 2Department of Radiology, Massachusetts General Hospital, Boston, MA, United States, 3Centre for Medical Image Computing, University College London, London, United Kingdom, 4Computer Science and Artificial Intelligence Laboratory, MIT, Cambridge, MA, United States
Synopsis
We introduce a novel strategy for learning deformable registration without acquired imaging data, producing networks robust to MRI contrast. While classical methods repeat an optimization for every new image pair, learning-based methods require retraining for accurate registration of unseen image types. To address these inefficiencies, we leverage a generative strategy for diverse synthetic label maps and images that enable training powerful networks that generalize to a broad spectrum of MRI contrasts. We demonstrate robust and accurate registration of arbitrary unseen MRI contrasts with a single network, thereby eliminating the need for retraining models.
Introduction
Deformable registration is a key component of neuroimaging pipelines and consists in computing a dense transform to morph an image into the space of another. In brain MRI, the same anatomy can have a dramatically different appearance depending on the pulse sequence. For example, while T1-weighted contrast (T1w) clearly delineates normal tissues, T2-weighting (T2w) excels at detecting abnormal fluids. Many applications hinge on registration of such images to compare separate subjects (within contrast) or for morphometric analysis in the space of an atlas, that might have a different contrast than the input image.Classical methods optimize an objective function that balances image similarity with field regularity. Unfortunately, this optimization needs to be repeated for every image pair. Learning methods learn a function that maps an image pair to a transformation, but these approaches do not generalize to data with contrast properties that differ from the training set. For example, networks trained on T1w pairs will typically not accurately register T2w image pairs.
We propose SynthMorph, a strategy addressing this dependency by learning registration from images of arbitrary geometric content and gray-scale intensity. We evaluate this strategy in an array of realistic spoiled gradient-echo contrasts obtained from Bloch-equation simulations and MPRAGE contrasts derived from MP2RAGE acquisitions.
Method
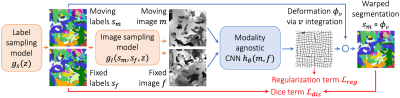
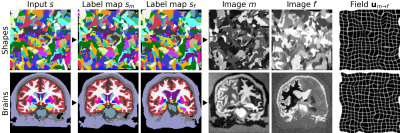
We build on VoxelMorph1, a U-Net2 that outputs a diffeomorphism3 $$$\phi$$$ (Figure 1). We fit network parameters by optimizing a loss $$$\mathcal{L}$$$ containing a dissimilarity term $$$\mathcal{L}_{dis}$$$ and a regularization term $$$\mathcal{L}_{reg}$$$: $$\mathcal{L}(m,f,\phi)=\mathcal{L}_{dis}(m\circ\phi,f)+\lambda\cdot\mathcal{L}_{reg}(\phi),$$ where $$$\lambda$$$ is a constant. To achieve contrast invariance, we synthesize arbitrary shapes and contrasts from pure noise models (Figure 2) and use these to train the network. At every mini batch, we synthesize two paired 3D label maps $$$\{s_m,s_f\}$$$. Alternatively, if brain segmentations are available, we deform two label maps from separate subjects. From $$$\{s_m,s_f\}$$$, we synthesize4 gray-scale images $$$\{m,f\}$$$: briefly, we sample intensities for each label using a Gaussian mixture model and randomly apply artifacts including blurring and an intensity bias field (Figure 3). We emphasize that no acquired images are used.The synthesis from label maps enables minimization of a loss function that measures volume overlap independent of image contrast:5 $$\mathcal{L}_{dis}(\phi,s_m,s_f)=1-\frac{2}{J} \sum_{j=1}^{J} \frac{|(s_m^j\circ\phi)\odot s_f^j|}{|(s_m^j\circ\phi)\oplus s_f^j|},$$ where $$$s^j$$$ is the one-hot encoded label $$$j\in\{1,2,...,J\}$$$ of label map $$$s$$$, and $$$\odot$$$ and $$$\oplus$$$ denote voxel-wise multiplication and addition, respectively.
Experiment
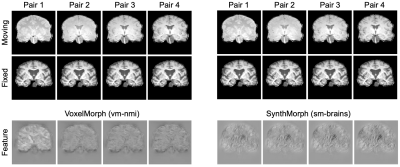
We assess robustness to MRI-contrast changes by registering a moving image with gradually varying contrast to a fixed T1w image and measuring label overlap as Dice coefficients. We test two SynthMorph variants: one trained only with images synthesized from random shapes (sm-shapes) and another model trained only with images synthesized from brain label maps (sm-brains).Data
We train our models on 40 distinct-subject segmentation maps with brain and non-brain labels derived from the Buckner40 dataset6. For each of 10 subject pairs, we compile a series of FLASH7 images with contrast ranging from proton-density weighted (PD) to T1w, using Bloch-equation simulations in acquired T1, T2* and PD maps: TR/TE 20/2 ms, FA {2,4,...,40}°. We also compile a series of MPRAGE images with TI {300,320,...,1000} ms from MP2RAGE8 acquisitions: TR/TE 5000/2.98 ms, TI1/TI2 2700/2500 ms, FA 4°. We derive brain and non-brain labels for training and evaluation using SAMSEG9, and map all images to a common affine space with 1 mm isotropic resolution.
Baselines
As classical baselines, we test ANTs/SyN10 with cost function MI, NiftyReg11 with cost function NMI, and the patch-similarity method deedsBCV12. As learning baselines, we train VoxelMorph (vm-ncc) with similarity loss NCC and the same architecture as our models, on 100 skull-stripped T1w images from HCP-A13,14. We train another VoxelMorph model with NMI on combinations of 100 T1w and 100 T2w images (vm-nmi).
Results
Figure 4 compares registration accuracy as a function of moving-image contrast. While results are similar across methods when both images have T1w contrast, as contrast differences increase, only our method remains robust, whereas ANTs, NiftyReg and VoxelMorph break down. Figure 5 shows example feature maps extracted from the last network layer illustrating this result.
Discussion
GeneralizabilityGeneralizability to unseen data types is a critical obstacle to the deployment of neural networks. Although methods such as VoxelMorph improve on classical registration accuracy, their weak point remains robustness to new image types unseen during training. We address this weakness by proposing a strategy for training networks to be robust to MRI-contrast changes.
Other body parts
While we focus on neuroimaging, our strategy promises to be extensible to other body parts. For example, accurate registration of cine-cardiac MRI frames is challenging due to low image quality but may facilitate insights into disease.15
Conclusion
We introduce a strategy for learning registration without acquired data. The approach yields unprecedented generalization accuracy for learning-based methods and enables registration of unseen MRI contrasts, which eliminates the need for retraining models. We encourage the reader to try out our code at http://voxelmorph.csail.mit.edu.Acknowledgements
The authors thank Douglas Greve and the HCP-A Consortium for sharing data. This research is supported by ERC Starting Grant 677697 and NIH grants NICHD K99 HD101553, NIA U01 AG052564, R56 AG064027, R01 AG064027, AG008122, AG016495, NIBIB P41 EB015896, R01 EB023281, EB006758, EB019956, R21EB018907, NIDDK R21 DK10827701, NINDS R01 NS0525851, NS070963, NS105820, NS083534, and R21 NS072652, U01 NS086625, U24 NS10059103, SIG S10 RR023401, RR019307, RR023043, BICCN U01 MH117023 and Blueprint for Neuroscience Research U01 MH093765. B. Fischl has financial interests in CorticoMetrics, reviewed and managed by Massachusetts General Hospital and Mass General Brigham.
References
1. Balakrishnan, G et al. VoxelMorph: A Learning Framework for Deformable Medical Image Registration. IEEE TMI. 2019;38(8):1788-00.
2. Ronneberger O et al. U-Net: Convolutional Networks for Biomedical Image Segmentation. CoRR. 2015;234-241.
3. Ashburner, J. A fast diffeomorphic image registration algorithm. NeuroImage. 2007;38(1):95-113.
4. Billot, B et al. A Learning Strategy for Contrast-agnostic MRI Segmentation. PMLR. 2020;121:75-93.
5. Milletari, F et al. V-net: Fully convolutional neural networks for volumetric medical image segmentation. 3DV. 2016:565-71.
6. Fischl, B et al. Whole brain segmentation: automated labeling of neuroanatomical structures in the human brain. Neuron. 2002;33(3):341-355.
7. Buxton, RB et al. Contrast in Rapid MR Imaging: T1- and T2-Weighted Imaging. J Comput Assist Tomogr. 1987;11(1):7-16.
8. Marques, J et al. MP2RAGE, a self bias-field corrected sequence for improved segmentation and T1-mapping at high field. NeuroImage. 2010;49(2)1271-81.
9. Puonti, O et al. Fast and sequence-adaptive whole-brain segmentation using parametric Bayesian modeling. NeuroImage. 2016;143(1):235-49.
10. Avants, BB et al. Symmetric diffeomorphic image registration with cross-correlation. Med Image Anal. 2008;12(1):1361-8415.
11. Modat, M et al. Fast free-form deformation using graphics processing units. Comput Meth Prog Bio. 2010;98(3):278-84.
12. Heinrich, M et al. MRF-based deformable registration and ventilation estimation of lung CT. IEEE TMI. 2013;32(7):1239-1248.
13. Harms, MP et al. Extending the Human Connectome Project across ages: Imaging protocols for the Lifespan Development and Aging projects. NeuroImage. 2018;183:972-984.
14. Bookheimer, SY et al. The Lifespan Human Connectome Project in Aging: An overview. NeuroImage. 2019;185:335-348.
15. Tavakoli, V and Amini, AA. A survey of shaped-based registration and segmentation techniques for cardiac images. Comput Vis Image Underst. 2013;117(9):966-989.
Figures