Introduction

Cardiac magnetic resonance imaging (MRI) is increasingly used in clinical practice, where a series of images are acquired during the scan to capture the cardiac dynamic. Fast imaging techniques are often adopted to improve temporal resolution, which may reduce signal-to-noise ratio of each time frame and making image denoising more necessary. However, dynamic imaging also provides more information for denoising as the images at different time frames have similar content and often follow the same noise model. In this work, we propose a deep learning framework for dynamic imaging denoising, where we explore similarity of image content at different time frames by performing image registration and utilize the fact that noises of different observations are independent and following similar noise model.

Methods

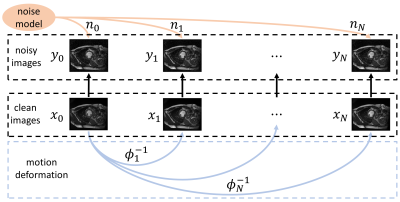
Let $$$y_0$$$ be the noisy image we want to denoise and $$$y_1, ..., y_N$$$ be $$$N$$$ extra noisy images at different time frames. Suppose the noisy images are generated under the data model in Fig.1.
$$y_k=x_k+n_k=x_0\circ\phi_k^{-1}+n_k, k=0,1,...,N$$
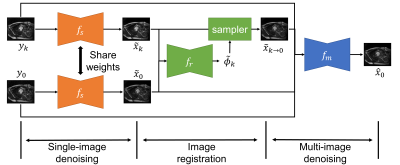
where $$$x_k$$$ and $$$n_k$$$ are the unknown clean image and noise respectively, and $$$\phi_k$$$ is the deformation field between the target frame and frame $$$k$$$. The task of self-supervised denoising is to estimate $$$x_0$$$ using information from the noisy images, $$$y_0, ..., y_N$$$. The overview of our proposed method is shown in Fig.2, which consists of the following three stages.

1) Single-image denoising: First we perform image denoising on each frame separately in a self-supervised manner, which serves as an initialization for the following stages. Inspired by Self2Self [1], given a noisy image $$$y_k$$$, we randomly sample a binary mask $$$b_k$$$ to mask out some pixels in $$$y_k$$$. Then a network $$$f_s$$$ is trained to recover the missing pixels based on information from the remaining pixels. The output of network, $$$\tilde{x}_{k} = f_s(b_k\odot y_k)$$$ is the denoised image. The network is trained by minimizing the mean squared error(MSE) between the network output and the noisy image on the masked pixels: $$\mathcal{L}_s=\frac{1}{N+1}\sum_{k=0}^N || (1-b_k)\odot (\tilde{x}_k-y_k) ||_2^2.$$

2) Image registration: we register the denoised image $$$\tilde{x}_k$$$, $$$k\in\{1,...,N\}$$$ to $$$\tilde{x}_0$$$. We adopt an unsupervised registration method based on Voxelmorph [2], where a network $$$f_r$$$ is used to prediction the deformation field given pairs of moving image $$$\tilde{x}_k$$$ and target image $$$\tilde{x}_0$$$, $$$\tilde{\phi}_k=f_r(\tilde{x}_k, \tilde{x}_0)$$$. The loss function for $$$f_r$$$ is as follows.
$$\mathcal{L}_r=\frac{1}{N}\sum_{k=1}^N || \tilde{x}_k\circ\tilde{\phi}_k -\tilde{x}_0 ||_2^2 + \lambda ||\nabla\tilde{\phi}_k||_2^2,$$
where $$$\lambda$$$ is a weighting coefficient. The first term is the similarity metric and the second term is a regularization for the deformation field.

3) Multi-image denoising: Let $$$\tilde{x}_{k\rightarrow0}=\tilde{x}_k\circ\tilde{\phi}_k$$$. In the final stage, we aggregate all these images to generate a refined estimation of the target clean image. We adopt the blind-spot method similar to the single-image denoising stage but concatenate all images as input and produce an estimation for the target frame.
$$\hat{x}_0 = f_m(\tilde{x}_0, \tilde{x}_{1\rightarrow0}, ..., \tilde{x}_{N\rightarrow0}, b\odot y_0, y_1, ..., y_N),$$
where $$$\hat{x}_0$$$ and $$$f_m$$$ is the final estimation and multi-image denoising network respectively. Again, we use a random binary mask $$$b$$$ to remove pixels in $$$y_0$$$, avoiding learning an identity mapping, and a masked MSE is used to train $$$f_m$$$,
$$\mathcal{L}_m=|| (1-b)\odot (\hat{x}_0-y_0) ||_2^2.$$

Our framework can be trained on a single scan without large-scale dataset. The total loss function for our proposed model is as follows: $$\mathcal{L}=\lambda_s \mathcal{L}_s +\lambda_r \mathcal{L}_r + \mathcal{L}_m.$$

Results

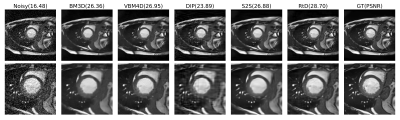
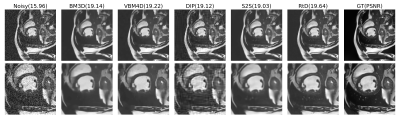
We simulate Gaussian noise and Rician noise in ACDC dataset[3], with $$$\sigma=5\%, 10\%$$$, and $$$15\%$$$. We compare our proposed method with other state-of-the-art denoising methods, including deep image prior(DIP)[4], Self2Self(S2S)[1], BM3D[5] and VBM4D[6]. We adopt PSNR and SSIM as evaluation metrics. Fig.3 shows the quantitative metrics of different methods on ACDC dataset for different noise settings. Fig.4 and 5 show example slices under Gaussian and Rician noise with $$$\sigma=15\%$$$ and the corresponding denoised results using different methods.

Discussion

As the quantitative results shown, the proposed method achieve comparable or even better performance than other methods for image denoising. Besides, comparing with S2S, our method outperforms it consistently, indicating that information from other time frames can largely boost performance of denoising models. The visualization results show that our method has not only better statistical but also better perceptual results compared with other methods. Single-image methods such as BM3D and Self2Self, only have access to one noisy observation, and therefore have not enough information to recover details that are corrupted by noise, resulting in blurred estimation. The DIP method suffers from significant structural artifacts in high noise levels. Though retrieving some details from adjacent frames, VBM4D also brings subtle artifacts to the denoised images, which degrade image quality. In comparison, the proposed method is able to recover more detail structures with higher image quality.

Conclusion

In summary, we proposed a self-supervised deep learning method for cardiac MRI denoising, which explores similarity of image content at different time frames by estimating the motion during imaging and improve image quality with sequential single- and multi-image denoising networks. Besides, the proposed method only trained on a single scan and has no prerequisite on large training dataset, making it practical for applications with scarce data. Experiments on a variety of noise settings show that our method has comparable or even better performance than other state-of-the-art unsupervised or self-supervised denoising methods.

Acknowledgements

No acknowledgement found.