Introduction

Diffusion-weighted MRSI (DW-MRSI) promises to significantly enhance in vivo tissue microstructural imaging by simultaneously measuring the diffusion properties of several molecules localized in specific tissue components^1-4. This unique capability provides rich compartment-specific⁵ and cell-specific microstructural information and potentially new disease biomarkers^6-7. However, DW-MRSI studies have been largely limited to single voxels or very low resolutions in basic science and clinical applications^8-10. This is because of the low sensitivity of MRSI and the extra SNR loss induced by diffusion encoding (DE), the high-dimensional imaging problem involving spatial, spectral, and diffusion dimensions, and the susceptibilities to system instability and physiological motions^3-4. While several fast acquisition methods have been proposed to accelerate DW-MRSI^9-10, the performance remains limited (e.g., >1cm³ resolution, single slices, and long imaging time)^8-10. We propose a novel method to enable high-resolution 3D DW-MRSI in a clinically relevant time, by synergizing a fast sequence with interleaved navigators and subspace-based processing¹¹. We have evaluated the proposed method using in vivo experiments and demonstrated high-SNR DW-MRSI of the brain and metabolite-specific ADC maps with the highest ever resolution (3.4×3.4×5.3 mm³).

Methods

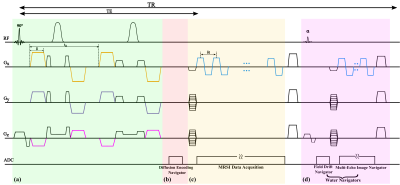
Data Acquisition: Acquiring high-resolution 3D DW-MRSI data in a clinically relevant time is rather challenging because of the additional encoding dimension, SNR consideration, the requirement of stronger DE gradients, and susceptibility to system instabilities and subject motions. Our proposed acquisition strategy addresses these issues by integrating a set of special features (illustrated in Fig.1). First, we adapted a recently proposed SPICE-based fast spatial-spectral encoding design with sparse (k,t)-space sampling capability to achieve rapid data collection with extended k-space coverage^11-12. Second, we used a combination of slab-selective excitation and an adiabatic refocusing pulse pair to minimize chemical-shift displacement errors (CSDEs) for spin-echoes while achieving excellent cortical coverage. Third, bipolar DE gradients were integrated into the refocusing scheme to realize large b-values without dramatically lengthening TEs¹³. Finally, several navigators were interleaved to allow for tracking and correcting phase inconsistencies induced by system instabilities and microscopic physiological motions while maximizing acquisition efficiency in each TR.
Data Processing: The proposed acquisition poses unique challenges for data processing, specifically, the problems of nuisance signal removal (NSRM) (compared to localized single voxels) and reconstruction from the high-resolution, noisy data. To this end, we proposed to use a union-of-subspaces (UoSS) model^14-16 to represent the high-dimensional DW-MRSI function of interest $$$\rho(\textbf{r},t,\textbf{b})$$$ as :
$$
\rho(\textbf{r},t,\textbf{b}) = \sum_{\textit{lw}=1}^{L_w}u_{lw}(\textbf{r},\textbf{b})\phi_{lw}(t) + \sum_{\textit{lf}=1}^{L_f}u_{lf}(\textbf{r},\textbf{b})\phi_{lf}(t) + \sum_{\textit{lm}=1}^{L_m}u_{lm}(\textbf{r})\phi_{lm}(t,\textbf{b}),[1]
$$
where $$$\phi_{lw}(t)$$$,$$$\phi_{lf}(t)$$$ are the water and lipid subspaces, respectively. $$$\phi_{lm}(t,\textbf{b})$$$ is the multi-b-value metabolite subspace($$$\textbf{b}$$$ denoting the DE space) and $$$u_x(\cdot)$$$ the corresponding spatial coefficients. Note that we proposed to use b-value independent water/lipid subspaces due to the nature of these signals. The multi-b-value metabolite subspace maximizes the representation power while maintaining the low dimensionality for the spatial coefficients^15-16. This model significantly reduces the dimensionality of the imaging problem and effectively exploits the correlations in the spectral-diffusion dimensions to enable better signal separation as well as resolution and SNR tradeoffs. Accordingly, we can fit water/lipid signals using these subspace constraints and remove their contributions from the data. The metabolite reconstruction can then be done by solving
$$
\left\{\hat{\textbf{U}},\hat{\textbf{V}}\right\} = \arg\underset{\textbf{U},\textbf{V}}{\min}\left\Vert\textbf{d}-\textbf{F}_{\Omega}\left\{\textbf{B}\odot\textbf{U}\textbf{V}\right\}\right\Vert_{2}^{2} + \lambda \mathcal{R}(\textbf{U}\textbf{V}),[2]
$$
where $$$\textbf{d}$$$ represents the data after NSRM, $$$\textbf{U}$$$ and $$$\textbf{V}$$$ are matrix forms of the spatial coefficients and multi-b-value subspace. $$$\textbf{B}$$$ models the B₀ inhomogeneity induced phases and $$$\textbf{F}$$$ the encoding operator with (k,t) sampling pattern $$$\Omega$$$ . $$$\mathcal{R(\cdot)}$$$ is a spatial-spectral regularization function with parameter $$$\lambda$$$ (e.g., joint sparsity)¹⁶. We predetermined $$$\textbf{V}$$$ from lower-resolution/higher-SNR data for reconstructing higher-resolution data with spatial-temporal undersampling^11-12. Phase discrepancies were extracted from both the DE and field drift navigators (Fig. 1) and corrected before NSRM. Figure 2 illustrates the correction effects (details omitted due to space constraint).

Results

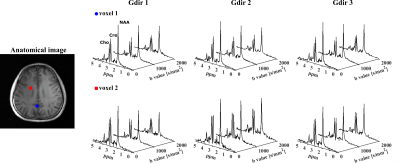
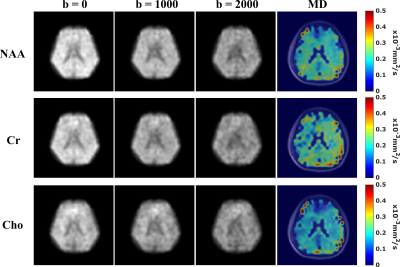
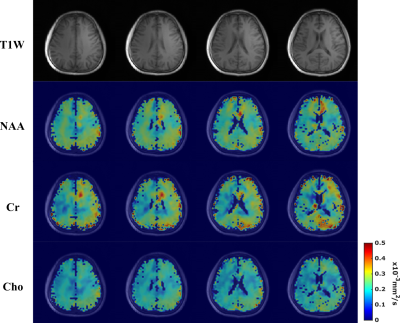
In vivo data were acquired from healthy volunteers on a Siemens Prisma 3T scanner using a 20-channel head coil. Cardiac gating was used to minimize the effects of microscopic tissue displacements due to pulsations (trigger delay = 200ms). Data at different resolutions were acquired with 220×220×64 mm³ FOV, 850/80 ms TR/TE, 167 kHz readout bandwidth, matrix sizes of 32x32x8 (6.9×6.9×8mm³ voxels) or 64x64x12 (3.4×3.4×5.3 mm³ voxels) and 0.8/1.18 ms echo spacing. The DE parameters are b-values = [0,1000,2000] s/mm², DW gradient duration $$$\delta$$$ = 10 ms, diffusion time $$$t_{d}$$$ = 38.8 ms. For the 32x32x8 data, we acquired 3 orthogonal diffusion directions, i.e.,[Gx,Gy,Gz] = [1,1,-0.5](Gdir1)/ [1,-0.5,1](Gdir2)/ [-0.5,1,1](Gdir3), with ~5mins per b-value. For the 64x64x12 data, only Gdir1 was acquired for the results shown here, taking around 16.5mins(retrospective undersampling, 25mins full acquisition). Figure 3 shows high-quality spatially-resolved DW spectra produced by the proposed method from 6.9×6.9×8mm³ voxels. The DW metabolite maps along with mean diffusivity (MD) maps are shown in Figure 4. High-SNR metabolite ADC maps produced from the 64x64x12 data are shown in Figure 5, demonstrating the capability of the proposed method in mapping microstructural information with unprecedented resolutions.

Conclusion

We presented a novel method to achieve high-resolution, 3D DW-MRSI that synergizes fast spatial-spectral encoding and subspace-based processing. High-quality reconstruction and metabolite-specific ADC maps of the human brain were successfully produced. These promising results demonstrate the potential of the proposed method to enable molecule-specific tissue microstructural imaging for various neuroscience and clinical applications.

Acknowledgements

No acknowledgement found.