0327
BUDA-STEAM: A rapid parameter estimation method for T1, T2, M0, B0 and B1 using three-90° pulse sequence1Korea Advanced Institute of Science and Technology, Daejeon, Korea, Republic of, 2Martinos Center for Biomedical Imaging, Charlestown, MA, United States
Synopsis
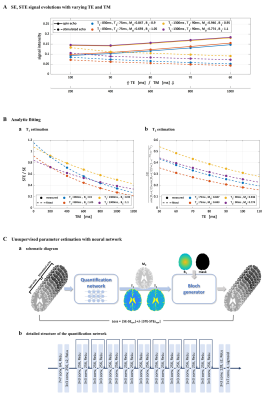
An MR parameter estimation method using spin- and stimulated-echo signals is proposed. Three-90° pulse sequence is introduced to simultaneously acquire spin and stimulated echo signals. These signals contain rich information that allow for estimation of T1, T2, M0, B0 and B1 maps. We utilize Blip Up-Down Acquisition (BUDA) to eliminate geometric distortion incurred by rapid EPI readout. In order to estimate the parameter maps from the spin- and stimulated-echo signals with high fidelity, two parameter estimation methods, analytic fitting and a novel unsupervised deep neural network method, are developed.
Introduction
MR parameter quantification enables advanced characterization of tissue and facilitates longitudinal studies1-4. However, MR parameter estimation techniques typically require excessive acquisition time, hence they often do not lend themselves to routine clinical application. Herein, we propose a rapid parameter estimation technique that provides distortion-free and co-registered T1, T2, M0, B0 and B0 maps.Method
Acquisition & ReconstructionThe proposed mapping of T1, T2, M0 and B1 inhomogeneity is based on simultaneously acquired spin- and stimulated-echo signals from three-90° RF pulse sequence5,6. Figure 1(a) shows the proposed pulse sequence, where EPI technique is used for rapidly encoding spin- and stimulated-echo contrasts. The acquired echo signals are formulated as follows:
$$S_{SE}=M_{0}\cdot(1-e^{-TR_{eff}^{prev}/T_{1}})\cdot sin(B_{1}\cdot \frac{\pi}{2})\cdot sin^{2}(B_{1}\cdot \frac{\pi}{4})\cdot e^{-TE/T_{2}}~~~~~[1]$$
$$S_{STE}=\frac{1}{2}\cdot M_{0}\cdot(1-e^{-TR_{eff}^{prev}/T_{1}})\cdot sin^{3}(B_{1}\cdot \frac{\pi}{2})\cdot e^{-TM/T_{1}}\cdot e^{-TE/T_{2}}~~~~~[2]$$
where TE is the echo time, TM is the mixing time, and $$$TR_{eff}^{prev}=TR^{prev}-\frac{TE^{prev}}{2}-TM^{prev}$$$ is the effective TR of the previous acquisition.
In order to eliminate the geometric distortion in the EPI readout, we introduce blip-up/down acquisition (BUDA) and reconstruction7. BUDA acquires two shots of EPI with opposite phase encoding directions. With this set of opposite-polarity images, B0 field map can be estimated8. BUDA reconstruction incorporates the estimated field inhomogeneity into parallel imaging forward model and employs Hankel structured low-rank constraint9-11 to exploits similarities between the opposite-polarity images while mitigating potential shot-to-shot phase variation as follows:
$$\min_{I}\sum_{t=1(blip-up)}^{2(blip-down)}‖F_{t}ECI_{t}-k_{t} ‖_{2}^{2}+\lambda‖\mathcal{H}(I)‖_{*}~~~~~[3]$$
where $$$F_{t}$$$ is Fourier operator in $$$t^{th}$$$ shot, $$$E$$$ is field inhomogeneity map, $$$C$$$ is coil sensitivities estimated from distortion-free gradient-echo calibration data using ESPIRiT12, $$$𝑘_{𝑡}$$$ is k-space data for $$$t^{th}$$$ shot, $$$\mathcal{H}(\cdot)$$$ is the block-Hankel representation and $$$𝐼$$$ is the distortion-free image.
While using a larger TM provides T1 sensitivity, this increases the dead time between the second and the third RF pulses and reduces the acquisition efficiency. We incorporate an echo-shifting approach6 to ensure high sampling efficiency, where the mixing time is used for acquiring spin echo data from different slice locations as shown in Figure 1(c).
Parameter estimation
We introduce two methods for estimating T1, T2, M0 and B1. First approach is an analytic method with dictionary matching and nonlinear least square fitting, whereas the second approach uses unsupervised neural network-based optimization.
Analytic fitting: We take the signal ratio between stimulated and spin echoes to eliminate T2 decay effect and spin density component.
$$\frac{S_{STE}}{S_{SE}}=\frac{1}{2}\cdot\left\{\frac{sin(B_{1}\cdot \frac{\pi}{2})}{sin(B_{1}\cdot \frac{\pi}{4})}\right\}^{2}\cdot e^{-TM/T_{1}}~~~~~[4]$$
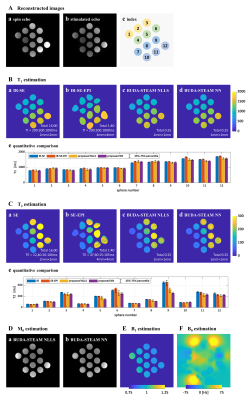
The ratio follows simple exponential decay with respect to TM. T1 and B1 are estimated from these ratio images. Rapid initial estimates for T1 and B1 are first obtained by Bloch-simulated dictionary matching and the values are used as seed point for subsequent nonlinear least-square fitting. The estimated T1 and B1 values are plugged in the spin echo signal equation, which now only contains T2 and M0 components and follows simple exponential decay with respect to TE. T2 and M0 are estimated by nonlinear least-square fitting after an interim dictionary matching. With the prior knowledge that B1 field is spatially smooth, B1 is estimated by polynomial fitting and T1 is re-estimated using the estimated B1 to improve estimation performance.
Unsupervised deep neural network for parameter estimation: In order to exploit spatial relations between neighboring voxels, we propose a convolutional neural network-based parameter quantification method. Input of the quantification network is a set of spin- and stimulated-echo images for various TE and TM. The quantification network produces T1, T2, M0 maps as output. A residual network is used as the quantification network. Starting from these output T1, T2, M0 maps and the polynomial fitted B1, spin- and stimulated-echo signals are synthesized by Bloch generator as Eqs [1-2]. The signal difference between the input images and the synthesized images is utilized as loss function, thereby obviating the need for any additional ground truth information during the estimation of network weights.
$$Loss=|SE-SE_{syn}|+\lambda|STE-STE_{syn}|~~~~~[5]$$
$$$\lambda$$$ is the regularizing parameter for compensating signal intensity difference between spin echo and stimulated echo signals.
Result
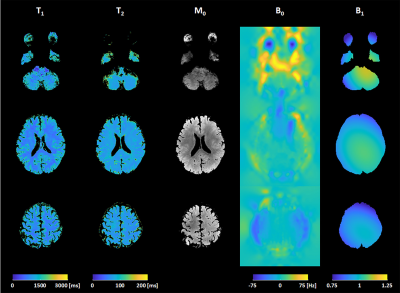
Phantom experiments and in vivo MRI experiments were conducted on 3T MRI scanner (Siemens Magnetom Verio) to validate the proposed method. The proposed simultaneous spin echo and stimulated echo acquisition was performed with five combinations of TE and TM.Parameter estimation results of phantom experiments with the proposed method and reference methods are shown in Figure 3 and those of in vivo brain experiments are shown in Figure 4 and 5. As shown in the parameter estimation results, geometric distortion are corrected by the proposed BUDA-STEAM. In terms of T1 and T2 values, the proposed and reference methods show similar results even though the proposed method took shorter time for acquisition, total 25sec for the phantom experiment and 50sec for the in vivo experiment. The estimated results with the analytic fitting and the neural network-based estimation are similar for all parameters of T1, T2, B1, and M0. The neural network-based estimation provides noise-robust MR parameters owing to the fact that the convolutional network takes information of spatially adjacent voxels into account.
Discussion & Conclusion
The proposed BUDA-STEAM parameter estimation method enables acquisition of distortion-corrected, co-registered T1, T2, M0, B1 and B0 maps, within a short acquisition time using a three-90° pulse sequence and BUDA reconstruction. In addition, the parameter estimation using unsupervised neural network optimization provided noise-robust results from this rapid acquisition.Acknowledgements
This research was supported by a grant of the Korea Health Technology R&D Project through the Korea Health Industry Development Institute (KHIDI), funded by the Ministry of Health & Welfare, Republic of Korea (grant number : HI14C1135) and MIT-Korea - KAIST Seed Fund of MIT International Science and Technology Initiatives (MISTI).References
[1] Tofts, Paul, ed. Quantitative MRI of the brain: measuring changes caused by disease. John Wiley & Sons, 2005.
[2] Neema, Mohit, et al. "T1‐and T2‐based MRI measures of diffuse gray matter and white matter damage in patients with multiple sclerosis." Journal of Neuroimaging 17 (2007): 16S-21S.
[3] Bohnen, Sebastian, et al. "Performance of t1 and t2 mapping cardiovascular magnetic resonance to detect active myocarditis in patients with recent-onset heart failure." Circulation: Cardiovascular Imaging 8.6 (2015): e003073.
[4] Foltz, Warren D., et al. "Changes in apparent diffusion coefficient and T2 relaxation during radiotherapy for prostate cancer." Journal of Magnetic Resonance Imaging 37.4 (2013): 909-916.
[5] Shi, Xianfeng, Seong‐Eun Kim, and Eun‐Kee Jeong. "Single‐shot T1 mapping using simultaneous acquisitions of spin‐and stimulated‐echo‐planar imaging (2D ss‐SESTEPI)." Magnetic resonance in medicine 64.3 (2010): 734-742.
[6] Fritz, Francisco J., Benedikt A. Poser, and Alard Roebroeck. "MESMERISED: Super-accelerated 7 T STEAM imaging for quantitative multi-contrast and diffusion MRI." bioRxiv (2020).
[7] Liao, Congyu, et al. "Highly efficient MRI through multi-shot echo planar imaging." Wavelets and Sparsity XVIII. Vol. 11138. International Society for Optics and Photonics, 2019.
[8] Andersson, Jesper LR, Stefan Skare, and John Ashburner. "How to correct susceptibility distortions in spin-echo echo-planar images: application to diffusion tensor imaging." Neuroimage 20.2 (2003): 870-888.
[9] Haldar, Justin P. "Low-rank modeling of local k-space neighborhoods (LORAKS) for constrained MRI." IEEE transactions on medical imaging 33.3 (2013): 668-681.
[10] Lee, Dongwook, et al. "Acceleration of MR parameter mapping using annihilating filter‐based low rank hankel matrix (ALOHA)." Magnetic resonance in medicine 76.6 (2016): 1848-1864.
[11] Mani, Merry, et al. "Multi‐shot sensitivity‐encoded diffusion data recovery using structured low‐rank matrix completion (MUSSELS)." Magnetic resonance in medicine 78.2 (2017): 494-507.
[12] Uecker, Martin, et al. "ESPIRiT—an eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA." Magnetic resonance in medicine 71.3 (2014): 990-1001.
Figures