0315
Partial Fourier Reconstruction in Liver DWI using a Recurrent Convolutional Network1Pattern Recognition Lab, Friedrich-Alexander-Universität Erlangen-Nürnberg, Erlangen, Germany, 2Magnetic Resonance, Siemens Healthcare GmbH, Erlangen, Germany
Synopsis
Partial Fourier (PF) acquisition allows to reduce TE in single-shot echo-planar imaging in order to increase signal-to-noise ratio (SNR) in diffusion-weighted imaging (DWI). However, when applying it to motion-prone liver DWI, conventional PF reconstruction methods fail since they rely on smoothness priors of the phase. This work proposes to use an unrolled network architecture which aims to estimate a more appropriate regularization by learned recurrent convolutions. It can be shown that reconstructions produced by the network are superior in terms of quantitative measures as well as qualitative impression compared to conventional methods which tend to introduce artifacts.
Introduction
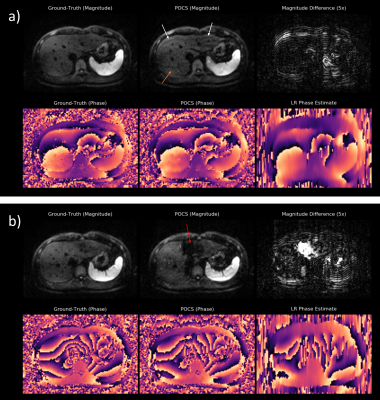
DWI is valuable for lesion detection and classification and is thus frequently used in clinical protocols for liver MRI [1,2]. However, the T2*-blurring of typically employed single-shot echo-planar imaging (ssEPI) combined with strong diffusion encoding leads to inherently SNR-starved images. PF-sampling along the phase-encoding direction is often employed to shorten the TE and to increase the apparent SNR.In order to reconstruct an image from an asymmetrically sampled k-space, conventional PF methods try to exploit Hermitian symmetry in frequency domain by assuming smoothness of the phase. Homodyne [3] and Projection Onto Convex Sets (POCS) [4] utilize a low-resolution (LR) phase prior which is estimated from the symmetrically sampled part around the k-space center. However, when applying these methods to liver DWI – which is often subject to rapid, motion-related phase variations – artifacts are introduced (Figure 1). The fact that currently no robust reconstruction method for PF-DWI of the liver exists, prevents its use in clinical practice or limits it to weak PF factors with relatively small SNR gains.
This work aims to enable the application of PF to liver DWI using an iterative reconstruction which, similar to POCS, alternates between regularizing the current estimate and enforcing data fidelity. However, instead of explicitly relying on smoothness assumptions of the phase, this work proposes to learn a more suitable regularizer from training data using a recurrent convolutional network.
Methods
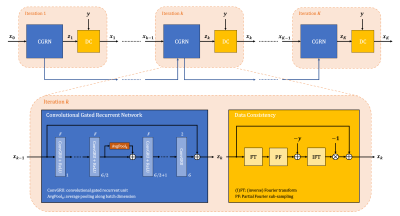
Network architecture: The employed network architecture is derived from unrolling a variational splitting algorithm for a fixed number of iterations. Within each iteration the algorithm alternates between gradient descent with respect to regularizer and data term, respectively, whereas the former is replaced by a neural network. The Deep Recurrent Partial Fourier Network (DRPF-Net) employed in this work was introduced in [5] and uses convolutional gated recurrent units [6] which conserve a memory state across iterations (Figure 2). This allows weight-sharing across iterations while maintaining the flexibility to adapt to iteration-specific conditions. While multiple repetitions of a slice were arranged into a 3-D stack in [5], they are now represented as a typical input batch allowing to employ 2-D instead of 3-D convolutions which are expensive with respect to both run-time and memory. In order to still exploit correlations across the repetitions and additionally ensure permutation-equivariance, the idea of Deep Sets [7] was employed by including pooling operations along the batch dimension.Data: Liver DWI (b-values: 50, 800 s/mm2) was acquired in 25 volunteers using a prototypical ssEPI sequence on 1.5 and 3 T MR scanners (MAGNETOM, Siemens Healthcare, Erlangen, Germany). Data was acquired without PF but with parallel acceleration (2x). Coil-combined, complex-valued ground-truth data was generated using a prototypically modified reconstruction pipeline. Data was divided into training (19 volunteers), validation (2) and test (4) sets comprising 665, 70 and 140 image slices, respectively. In addition to that, one data set was acquired using prospective PF-sampling (5/8).
Training: During training, complex images were retrospectively sub-sampled with a PF-factor of 5/8 and then fed to the network as a two-channel input representing real and imaginary part, respectively. The training objective was to minimize a loss function consisting of two terms: a pixel-wise L1-loss and a perceptual loss [8], where the former was weighted twice as high. Optimization was performed using Adam [9] with a learning rate of 10-4 for 200 epochs.
Evaluation: The reconstructions produced by the DRPF-Net and POCS (each using 5 iterations) were evaluated both quantitatively and qualitatively on retrospectively sub-sampled data. For qualitative analysis, results on the prospectively PF-sampled data set were assessed as well. All evaluations were performed on the averaged DW images and for a PF factor of 5/8.
Results & Discussion
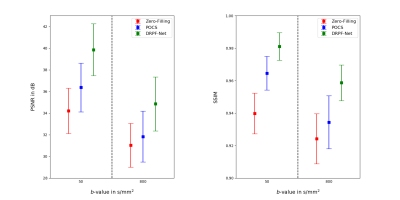
The qualitative comparison for retrospectively sub-sampled data is presented in Figure 3. While the zero-filled reconstruction is significantly blurred, POCS alleviates blurring but introduces signal fluctuations and artificial structures due to the underlying LR phase estimate. In contrast, the DRPF-Net produces sharp reconstructions without noticeable artifacts. This is substantiated by the results of the quantitative evaluation (Figure 4) as the DRPF-Net outperforms zero-filling and POCS significantly with respect to peak signal-to-noise ratio (PSNR) and structural similarity (SSIM) for both b-values.Figure 3 additionally demonstrates that the location in the left liver lobe which suffers from artifacts in the POCS reconstruction coincides with strong phase variations which cannot be reconstructed accurately as shown for a selected repetition. In contrast, the phase map produced by the DRPF-Net is in higher agreement with the ground-truth indicating the method’s capability to recover high-frequency phase information even at high degrees of asymmetry.
The performance on prospectively sub-sampled data can also be validated as Figure 5 demonstrates the network’s ability to reconstruct visually appealing images with homogeneous liver signal and high resolution with respect to small structures like vessels.
Conclusion
This work demonstrates that PF-reconstruction of motion-affected liver DWI is possible using an unrolled network architecture. Due to the elimination of phase priors unsuitable for the given application and the employment of learned recurrent convolutions, the proposed method produces quantitatively and qualitatively convincing reconstructions. Realizing liver DWI with significantly reduced echo-train length can enable increased SNR and TE-intensive schemes such as bipolar or flow-compensated diffusion preparation, for example.Acknowledgements
No acknowledgement found.References
[1] Mitchell, D. G., Bruix, J., Sherman, M., & Sirlin, C. B. (2015). LI‐RADS (Liver Imaging Reporting and Data System): Summary, discussion, and consensus of the LI‐RADS Management Working Group and future directions. Hepatology, 61(3), 1056-1065.
[2] Taouli, B., & Koh, D. M. (2010). Diffusion-weighted MR imaging of the liver. Radiology, 254(1), 47-66
[3] Noll, D. C., Nishimura, D. G., & Macovski, A. (1991). Homodyne detection in magnetic resonance imaging. IEEE transactions on medical imaging, 10(2), 154-163.
[4] Haacke, E. M., Lindskogj, E. D., & Lin, W. (1991). A fast, iterative, partial-Fourier technique capable of local phase recovery. Journal of Magnetic Resonance (1969), 92(1), 126-145.
[5] Gadjimuradov, F., Benkert, T., Nickel, M. D., & Maier, A. (2020). Deep Recurrent Partial Fourier Reconstruction in Diffusion MRI. In International Workshop on Machine Learning for Medical Image Reconstruction (pp. 38-47). Springer, Cham.
[6] Ballas, N., Yao, L., Pal, C., & Courville, A. (2015). Delving deeper into convolutional networks for learning video representations. arXiv preprint arXiv:1511.06432.
[7] Zaheer, M., Kottur, S., Ravanbakhsh, S., Poczos, B., Salakhutdinov, R. R., & Smola, A. J. (2017). Deep sets. Advances in neural information processing systems, 30, 3391-3401.
[8] Zhang, R., Isola, P., Efros, A. A., Shechtman, E., & Wang, O. (2018). The unreasonable effectiveness of deep features as a perceptual metric. In Proceedings of the IEEE conference on computer vision and pattern recognition (pp. 586-595).
[9] Kingma, D. P., & Ba, J. (2014). Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980.
[10] Maier, A. K., Syben, C., Stimpel, B., Würfl, T., Hoffmann, M., Schebesch, F., ... & Christiansen, S. (2019). Learning with known operators reduces maximum error bounds. Nature machine intelligence, 1(8), 373-380.
Figures