Introduction

Recently, a rise in the popularity of deep learning-based methods has coincided with a shift away from shallower dictionary-based methods for regularization in MR image reconstruction. A probable cause for this trend may be an underlying assumption that features learned using relatively unrestricted supervised deep models subsume those learned in a 'blind' fashion (learned from measurements of the image without any additional training data), and other sparsity-based priors that are deemed “handcrafted”. However, it is unknown if this assumption is valid, even when supervised deep learning methods can learn very rich models for reconstructing MR images. Moreover, deep CNNs often require relatively large datasets to train well.
This work seeks to address both these issues by studying the processes of blind dictionary learning-based and supervised learning-based MRI reconstruction from under-sampled data and highlighting the complementarity of the two approaches by proposing a framework that combines the two in a residual fashion. We also study the demand for training data for our proposed method, compared to strict deep supervised reconstruction.

Problem Setup and Algorithm

In model-based regularized reconstruction approaches, given a set of k-space measurements $$$y_c \in \mathbb{C}^p, \ c=1, \ldots, N_c,$$$ from $$$N_c$$$ coils with corresponding system matrices $$$A_c \in \mathbb{C}^{p \times q}, \ c=1, \ldots, N_c$$$, the image $$$x\in\mathbb{C}^{q\times q}$$$ is obtained by optimizing a cost function of the form:
$$\underset{x}{\arg\min} ~ \nu \sum_{c=1}^{N_c} \|A_c x - y_c\|_2^2 + \mathcal{R}(x). $$
For blind dictionary-learning based reconstruction the regularizer has the form [2],
$$\mathcal{R}(x)=\underset{D, Z}{\min}~\sum_{j=1}^{N_1}\|\mathcal{P}_j{x}-Dz_j\|_2^2+\lambda^2\|z_j\|_0\qquad\text{s.t.}\qquad \|d_u\|_2=1~~\forall~u,$$
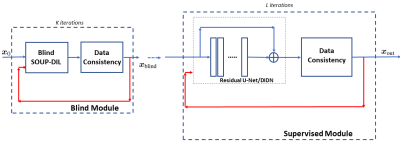
where $$$D\in\mathbb{C}^{n\times J}$$$ is an overcomplete dictionary whose $$$u$$$th column is $$$d_u$$$, $$$Z\in\mathbb{C}^{J\times N_1}$$$ is a sparse code matrix whose columns are $$$z_j$$$, and $$$\mathcal{P}_jx\in\mathbb{C}^{n\times N_1}$$$ is the $$$j$$$th $$$(\sqrt{n}\times\sqrt{n})$$$ overlapping patch in $$$x$$$ extracted as a vector. A typical approach to solving this blind dictionary learning reconstruction problem alternates between updating the dictionary and sparse representation using the current estimate of the image $$$x$$$, and then updating the reconstructed image [2]. Let $$$B^{i}(\cdot)$$$ denote the function representing the $$$i$$$th iteration of this alternating algorithm, and $$$x_i$$$ be the reconstructed image at the start of the iteration, then $$$x_{i+1} = B^{i}(x_i)$$$.
Applying $$$K$$$ such iterations, we have:
$$x_{\text{blind}}=x_K=B^{K}\circ B^{K-1}\circ\ldots B^{1}(x_0),$$
where $$$\circ$$$ represents function composition. Similarly, for data-consistent reconstruction using a supervised deep-residual network, like MoDL [1] the regularizer has the form
$$\mathcal{R}(x)=\|x-\big(D_{\theta}(\bar{x})+\bar{x}\big)\|_2^2,$$
where $$$D_{\theta}(\cdot)$$$ is a CNN-based denoiser, and $$$\bar{x}$$$ is its input. Again, if $$$S^{l}_{\theta}(\cdot)$$$ is the $$$i$$$th iteration of the algorithm that solves this deep learning-based regularized inverse problem, we have:
$$x_{l+1}=S^{l}_{\theta}(x_l)=\underset{x}{\arg\min}~\nu \sum_{c=1}^{N_c} \|A_c x - y_c\|_2^2+\|x-\big(D_\theta(\bar{x}_l)+\bar{x}_l\big)\|_2^2.$$
After $$$L$$$ 'iterations' of supervised reconstruction,
$$x_{\text{supervised}}=x_L=S^{L}_{\theta}\circ S^{L-1}_{\theta}\circ\ldots S^{1}_{\theta}(x_0).$$
Usually, the network weights $$$\theta$$$ are learned from pairwise training data consisting of undersampled measurements and corresponding ground truth images using a mean squared error or mean absolute error loss. We propose combining shallow sparsity-based reconstruction and deep supervised learning reconstruction in the following manner:
$$\hat{x}=S_{\theta}^L\circ\ldots\circ S_{\theta}^1\circ B^K\circ\ldots B^1(x_0)=\mathcal{M}_{\theta}(x_0)$$
Fig. 1 shows the corresponding pipeline. Essentially, we use the result of the blind dictionary learning-based reconstruction algorithm as a foundation for the deep supervised reconstruction to residually refine.

Methods

We use the SOUP-DIL algorithm [2] for dictionary learning-based reconstruction $$$(\nu=8\times10^{-4},\lambda=0.2)$$$, and used pairwise training data from the fastMRI knee dataset [3] to train the deep supervised network ($$$\nu=2$$$). The training loss function was:
$$\hat{\theta}=\underset{\theta}{\arg\min}\sum_{n=1}^{N_2}\big(\big\|x_{\text{true}}^{(n)}-\mathcal{M}_{\theta}(x_0^{(n)})\big\|_2^2+\beta\big\|x_{\text{true}}^{(n)}-\mathcal{M}_{\theta}(x_0^{(n)})\big\|_1\big),$$ where $$$n$$$ indexes the training data, and a DIDN [4] architecture was used for $$$\theta$$$ with a batch size of 4. Conjugate gradient method was used for the image update for both the deep supervised and blind dictionary-based reconstruction schemes.
We compared the proposed method against strict supervised learning for reconstruction using the 5-fold undersampling mask shown in Fig. 2. The metrics used for evaluation were PSNR (in dB), SSIM, and HFEN (High-Frequency Error Norm [5]). We also varied the size of the training dataset to validate the robustness of the performance of both methods to the availability of training data.

Results

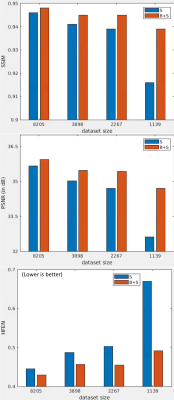
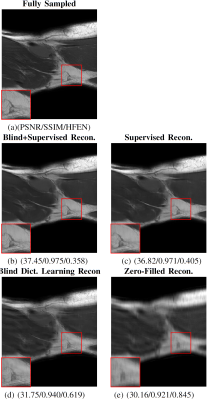
Fig. 3 shows the results on a test set of 513 slices across various training dataset sizes. BLIPS reconstruction outperforms strict supervised learning-based reconstruction across all metrics and training dataset sizes. BLIPS performance is also much more robust to the availability of training data, and can yield much better quality reconstructions with limited training data. This robustness is evident in Fig 4, which visualizes the comparisons of performance (across training dataset sizes) in Fig 3 through separate bar graphs for SSIM, PSNR and HFEN.
Fig. 5 visualizes the performance of supervised, blind, and BLIPS reconstructions on a test image slice. It is evident that combining blind dictionary-based learning with supervised learning retains several 'fine' details in the image which are smoothed/blurred out in a strict supervised reconstruction. We hypothesize this is because patch-based instance adaptive dictionary learning-based reconstruction restores these features, which are then refined by deep residual supervised learning-based reconstruction.

Conclusions

We conclude that there is significant complementarity between the features learned by deep supervised models and those traditionally deemed "handcrafted" or learned in a blind fashion, and there are significant benefits to combining these two models for MR image reconstruction.

Acknowledgements

This work was supported in part by NSF Grant IIS 1838179 and NIH Grant R01 EB023618.