0277
DSLR+: Enhancing deep subspace learning reconstruction for high-dimensional MRI
Christopher Michael Sandino1, Frank Ong2, Ke Wang3, Michael Lustig3, and Shreyas Vasanawala2
1Electrical Engineering, Stanford University, Stanford, CA, United States, 2Radiology, Stanford University, Stanford, CA, United States, 3Electrical Engineering and Computer Sciences, UC Berkeley, Berkeley, CA, United States
1Electrical Engineering, Stanford University, Stanford, CA, United States, 2Radiology, Stanford University, Stanford, CA, United States, 3Electrical Engineering and Computer Sciences, UC Berkeley, Berkeley, CA, United States
Synopsis
Unrolled neural networks (UNNs) have enabled state-of-the-art reconstruction of dynamic MRI data, however, they remain limited by GPU memory hindering applications to high-resolution, high-dimensional imaging. Previously, we proposed a deep subspace learning reconstruction (DSLR) method to reconstruct low-rank representations of dynamic imaging data. In this work, we present DSLR+, which improves upon DSLR by leveraging a locally low-rank model and a more accurate data consistency module. We demonstrate improvements over state-of-the-art UNNs with respect to 2D cardiac cine image quality and reconstruction memory footprint, which is greatly reduced by reconstructing compressed representations of the data instead of the data itself.
Introduction
Unrolled neural networks (UNNs) have enabled learning of iterative procedures for recovery of dynamic MR images from vastly undersampled measurements1-3. However, UNN training remains limited by GPU memory constraints thus hindering applications to high-resolution and high-dimensional imaging. To address this, we previously proposed a deep subspace learning reconstruction (DSLR) framework, which uses low-dimensional neural networks to iteratively reconstruct compressed, low-rank representations of high-dimensional MRI data instead of the data directly4. While DSLR grants significant improvements to reconstruction time and GPU memory requirements, it does not surpass state-of-the-art UNNs with respect to image quality.In this work, we propose a new reconstruction framework, DSLR+, which extends the original DSLR with two main developments: 1) a locally low-rank model to represent spatially localized dynamics with higher fidelity, and 2) an enhanced data consistency module which fully inverts the MRI model within each unrolled iteration.
Theory
The original DSLR aims to reconstruct compressed representations obtained by decomposing dynamic MRI data into a product of simpler spatial and temporal basis functions (Fig 1A). This is known as a globally low-rank (GLR) model5, which has been demonstrated to be effective at representing global contrast changes, but not spatially localized dynamics commonly found in cardiac cine images. Instead, DSLR+ uses a locally low-rank (LLR) model6 to reduce temporal blurring of rapidly moving structures which cannot be captured by the GLR model (Fig 1B).Block-wise basis functions, $$$L_b$$$ and $$$R_b$$$, are jointly estimated by iteratively solving the following non-convex optimization problem:
$$\underset{L_b, R_b}{\text{argmin}}\big|\big|Y-A\sum_bM_b(L_bR_b^H)\big|\big|_F^2+\sum_b\Psi(L_b)+\Phi(R_b)\tag{Eq. 1}$$where $$$Y$$$ is the raw k-space data, $$$M_b$$$ converts blocks to the image representation, and $$$A$$$ is the MRI model comprised of ESPIRiT7 maps, Fourier transform, and k-space sampling mask. $$$\Psi$$$ and $$$\Phi$$$ are regularizers whose proximal operators are modelled by convolutional neural networks (CNNs). In DSLR, Eq. 1 is solved by an unrolled alternating minimization (AltMin) approach which alternates between proximal gradient descent (PGD) steps with respect to $$$L_b$$$ and $$$R_b$$$. However, because Eq. 1 is inherently ill-posed, PGD may not be suitable to efficiently solve this optimization problem. Inspired by the MoDL network architecture8, DSLR+ inverts the MRI model in each AltMin step to enhance data consistency steps in between CNN updates:
$$L_b^{(k+1/2)}=\underset{L_b}{\text{argmin}}\big|\big|Y-A\sum_bM_b(L_bR_b^{(k)H})\big|\big|_F^2\tag{Eq. 2}$$$$L_b^{(k+1)}=\text{CNN}_{2D}\big(L_b^{(k+1/2)}\big)\tag{Eq. 3}$$$$R_b^{(k+1/2)}=\underset{R_b}{\text{argmin}}\big|\big|Y-A\sum_bM_b(L_b^{(k)}R_b^{H})\big|\big|_F^2\tag{Eq. 4}$$$$R_b^{(k+1)}=\text{CNN}_{1D}\big(R_b^{(k+1/2)}\big)\tag{Eq. 5}$$Since Eqs. 2&4 are linear with respect to the optimization variables $$$L_b$$$ and $$$R_b$$$, a globally optimal solution can be found by the conjugate gradient (CG) algorithm for each unrolled iteration $$$k$$$.
Methods
Network Architecture: The proposed DSLR+ network is formed by unrolling Eqs. 2-5 to a fixed number of iterations, and training it end-to-end to learn an iterative procedure for reconstructing the block-wise basis functions (Fig. 2). The entire network is trained in a supervised fashion using the average $$$l_1$$$-loss between the DSLR+ network output and the fully-sampled reference images. The network is implemented in PyTorch9, and trained using the Adam optimizer10.Training Data: With IRB approval, fully-sampled bSSFP 2D cardiac CINE datasets are acquired from 15 volunteers at different cardiac views and slice locations on GE (Waukesha, WI) scanners. For training, 12 volunteer datasets are split slice-by-slice to create 190 unique cine slices, which are further augmented by random flipping, cropping along readout, and variable-density k-t undersampling (R=10-15). Two volunteer datasets are used for validation, and the remaining dataset is used for testing. One additional prospectively undersampled dataset is collected from a pediatric patient for testing.
Evaluation: We compare three different UNNs with respect to reconstruction speed and standard image quality metrics (PSNR, SSIM):
- MoDL8: Unrolled variable splitting network with five outer-loop iterations containing 2D+time ResNets11, 64 features/convolution. Ten inner-loop (CG) iterations are used to perform each model inversion.
- DSLR4: Unrolled AltMin-PGD network with five iterations containing 2D spatial and 1D temporal ResNets, 256 features/convolution, 8 basis functions, overlapping blocks of size 16x16.
- DSLR+: Unrolled AltMin-CG network with five outer-loop iterations containing 2D spatial and 1D temporal ResNets, 256 features/convolution, 8 basis functions, overlapping blocks of size 16x16. Twenty inner-loop (10 CG-$$$L_b$$$ + 10 CG-$$$R_b$$$) iterations are used to perform each model inversion.
Results
During network training, DSLR+ converges much faster than DSLR, but only slightly faster than MoDL (Fig. 3). The average reconstruction times for MoDL, DSLR, and DSLR+ are 1.33±0.06, 0.33±0.05, and 1.34±0.09 sec/slice respectively. The proposed DSLR+ depicts superior image quality in reconstructions of 14X retrospectively undersampled data compared to both MoDL and DSLR (Fig. 4). In reconstructions of 12X prospectively undersampled data, DSLR+ and MoDL show comparable image quality, although, DSLR+ shows slightly better de-aliasing performance (Fig. 5).Discussion & Conclusion
Many recent works have incorporated low-rank regularization as an additional signal prior to enhance UNN reconstruction12,13. The DSLR method is the first to leverage low-rank structure to reduce the memory footprint of UNN training. Here, we improve the original DSLR by introducing an LLR model, and integrating conjugate gradient steps for enhanced data consistency. While both additions increase computational complexity compared to DSLR, DSLR+ retains its small memory footprint during training and inference with drastically improved image quality.Acknowledgements
This work was supported by NIH R01EB009690, NIH R01EB026136, GE Healthcare, and the NSF Graduate Research Fellowship.References
- Schlemper J, Caballero J, Hajnal JV, Price A, Rueckert D. A Deep Cascade of Convolutional Neural Networks for Dynamic MR Image Reconstruction. IEEE Trans Med Imaging. 2018;37(2):491–503. doi:10.1007/tmi.2017.2760978
- Biswas S, Aggarwal HK, Jacob M. Dynamic MRI using model‐based deep learning and SToRM priors: MoDL‐SToRM. Magn Reson Med. 2019;82(1):485-494. doi:10.1002/mrm.27706
- Sandino CM, Lai P, Vasanawala SS, Cheng JY. Accelerating cardiac cine MRI using a deep learning‐based ESPIRiT reconstruction. Magn Reson Med. 2021;85(1):152-167. doi:10.1002/mrm.28420
- Sandino CM, Ong F, Vasanawala SS. Deep subspace learning: Enhancing speed and scalability of deep learning-based reconstruction of dynamic imaging data. In: Proceedings of the ISMRM & SMRT Virtual Conference & Exhibition. 2020.
- Liang ZP. Spatiotemporal imaging with partially separable functions. In: Proceedings of the 4th IEEE International Symposium on Biomedical Imaging: From Nano to Macro. 2007. doi:10.1109/nfsi-isbi.2007.4387720
- Trzasko JD, Manduca A. Local versus global low-rank promotion in dynamic MRI series reconstruction. In: Proceedings of the 19th Annual Meeting of the International Society of Magnetic Resonance in Medicine. Montreal, Quebec, Canada; 2011.
- Uecker M, Lai P, Murphy MJ, et al. ESPIRiT - An eigenvalue approach to autocalibrating parallel MRI: Where SENSE meets GRAPPA. Magn Reson Med. 2014;71(3):990–1001. doi:10.1002/mrm.24751
- Aggarwal HK, Mani MP, Jacob M. MoDL: Model-Based Deep Learning Architecture for Inverse Problems. IEEE Trans Med Imaging. 2019;38(2):394-405. doi:10.1109/tmi.2018.2865356
- Paszke A, Gross S, Massa F, et al. PyTorch: An imperative style, high-performance deep learning library. In: Advances in Neural Information Processing Systems. 2019:8024–8035.
- Kingma DP, Ba JL. Adam: A method for stochastic gradient descent. In: Proceedings of the 3rd International Conference on Learning Representations. San Diego, CA, United States; 2015.
- He K, Zhang X, Ren S, Sun J. Identity Mappings in Deep Residual Networks. In: Proceedings of the 14th European Conference on Computer Vision. Amsterdam, Netherlands. 2016:630-645. doi:10.1007/978-3-319-46493-0_38
- Pramanik A, Aggarwal HK, Jacob M. Deep Generalization of Structured Low-Rank Algorithms (Deep-SLR). IEEE Trans Med Imaging. 2020;39(12):4186-4197. doi:10.1109/tmi.2020.3014581
- Ke Z, Huang W, Cheng J, et al. Deep Low-rank Prior in Dynamic MR Imaging. arXiv :2006.12090 [cs, eess]. 2020.
Figures
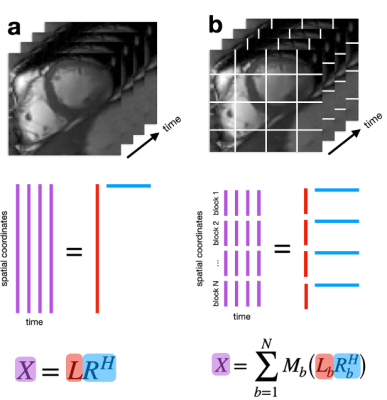
Fig. 1: (a) Each time frame is concatenated to form a 2D matrix. The globally low-rank (GLR) model assumes that this matrix is low-rank and can be represented as a product of two matrices containing relatively few basis functions. (b) The image is divided into blocks, then decomposed into a product of two matrices containing block-wise spatial and temporal basis functions. This locally low-rank (LLR) model generalizes GLR by exploiting spatially localized low-rank structure. Although non-overlapping blocks are shown, overlapping blocks are used to reduce blocking artifacts.
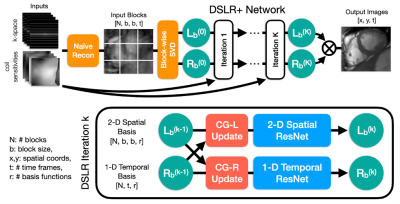
Fig. 2: Undersampled k-space data are reconstructed by zero-filling and then converted into blocks, which are decomposed using SVD to initialize $$$L_b$$$ and $$$R_b$$$. These are iteratively processed by DSLR+ by alternating conjugate gradient and CNN updates. Before each CNN, the basis functions are split into real/imaginary parts and concatenated along the featuredimension. For simplicity, 2-D and 1-D ResNets comprised of 6 convolutions each are used. At the end of the network, the basis functions are combined to form the output images.
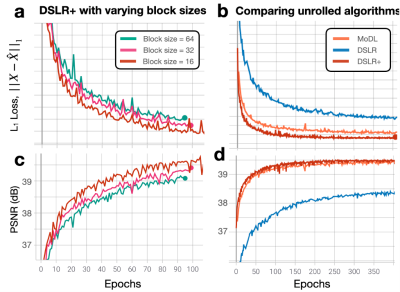
Fig. 3: (a,c) L1 loss and PSNR metrics are evaluated on the validation set for separate DSLR+ networks trained with block sizes of 16, 32, and 64 As the block size is decreased, both L1 loss and PSNR are improved because the LLR model has more degrees of freedom to represent the underlying image dynamics. (b,d) L1 loss and PSNR metrics are evaluated on the validation set for MoDL, DSLR, and DSLR+ networks. The DSLR+ network shows better metric performancecompared to original DSLR, suggesting that model inversion allows the network to converge to a solution quicker than with simpler PGD steps.
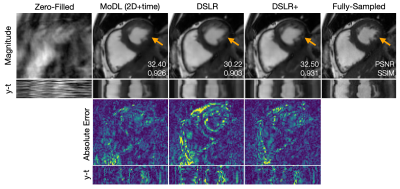
Fig. 4: A fully-sampled dataset is retrospectively undersampled by 14X using a variable-density k-t sampling pattern. This data is then reconstructed using (from left-to-right): zero-filling, MoDL, DSLR, and DSLR+ methods. Magnitude, errors, and y-t profiles are shown. PSNR and SSIM metrics are computed within an ROI around the heart and displayed on top of magnitude images. The proposed DSLR+ shows superior performance with respect to image quality metrics. Additionally, DSLR+ provides sharper definition of small papillary muscles compared to MoDL and DSLR (orange arrows).
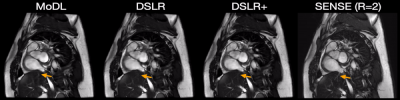
Fig. 5: Two prospectively undersampled scans are performed in a patient with premature ventricular contractions (PVC), which manifests as a double heartbeat motion. The first acquisition is 12X accelerated and reconstructed using MoDL, DSLR, and DSLR+ (left to right). A second acquisition is 2X accelerated and reconstructed with SENSE (rightmost). All show remarkable image quality despite severe acceleration, and never having seen a PVC during training. Both MoDL and DSLR+ faithfully demonstrate the double beat motion, although, DSLR+ depicts less residual aliasing (arrows).