0229
Joint Data Driven Optimization of MRI Data Sampling and Reconstruction via Variational Information Maximization1Stanford University, Stanford, CA, United States
Synopsis
We propose a framework for learning the sampling pattern in MRI jointly with reconstruction in a data-driven manner using variational information maximization. We enable optimization of k-space samples via continuous parametrization of the sampling coordinates in the non-uniform FFT operator. Experiments with knee MRI shows improved reconstruction quality of our data-driven sampling over the prevailing variable-density sampling, highlighting possible benefits that can be obtained by learning data sampling patterns.
Introduction
Deep learning methods have shown great promise at solving MR reconstruction problems. However, typically the sampling trajectories for accelerated MR imaging are first selected heuristically, and then the reconstruction networks are optimized separately. In other words, the reconstruction models are optimized for a pre-determined acquisition model without taking advantage of possible gains that can be obtained from learning the undersampling patterns.Recently, end-to-end deep learning methods have been proposed for learning undersampling patterns for MRI reconstruction problems. Active acquisition strategies1-3 make use of the previously acquired samples to determine the new samples to collect on-the-fly. The non-active strategies 4-7 produce undersampling masks or sampling trajectories, after which the learned sampling pattern is fixed and new scans can be acquired using the learned trajectory.
In this work, we consider the non-active case and present a variational information maximization method that enables joint optimization of acquisition and reconstruction of MRI scans in a end-to-end manner using deep uncertainty autoencoders.
Methods
We consider the MR signal model under the additive white complex Gaussian noise as $$z=f_\phi(x)+\epsilon=\big[(F_{nu}(\phi)S_1)^H\:\ldots\:(F_{nu}(\phi)S_C)^H\big]^Hx+\epsilon$$ where $$$x\in\mathbb{C}^N$$$ is the image, $$$z\in\mathbb{C}^M$$$ is the measurement in k-space, $$$f_\phi(\cdot)$$$ is the forward model that describes the imaging system parameterized by k-space sample coordinates $$$\phi\in[-0.5,0.5]^M$$$, and $$$\epsilon\sim\mathcal{N}_c(0,\sigma^2I)$$$ is the measurement noise. We further consider the multi-channel case with $$$C$$$ channels, where $$$S_i\in\mathbb{C}^{N\times N}$$$ is a diagonal matrix containing coil sensitivity profiles for coil $$$i$$$, and $$$F_{nu}(\phi):\mathbb{C}^N\rightarrow\mathbb{C}^{M/C}$$$ is the non-uniform FFT (nuFFT) operator at sampling locations $$$\phi$$$. Using the nuFFT operator parameterized by sampling locations ($$$\phi$$$) allows continuous optimization of sampling coordinates.Given an acceleration factor $$$R=N/M$$$, our goal is to find the optimal set of samples $$$\phi$$$ along with a reconstruction function $$$g(z)$$$ that produces high reconstruction quality. Under this setting, we adapt the uncertainty autoencoder framework defined in 8 and make use of the InfoMax principle9 that maximizes the mutual information between the image and noisy latent representations(k-space):
$$\begin{align}\max_\phi{I_\phi(X,Z)}&=\max_\phi{H(X)}-H_\phi(X|Z)\\&=\max_\phi{E_{q_{\phi}(X,Z)}}[\log q_\phi(X|Z)]\\&\geq\max_{\phi,\theta}E_{q_{\phi}(X,Z)}[\log p_\theta(X|Z)]\end{align}$$
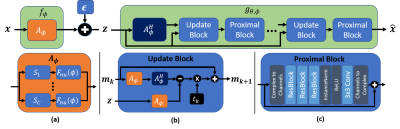
where in the last line we introduce a variational approximation to the model posterior to obtain a lower bound. The variational parameters $$$(\theta)$$$ correspond to the weights of the reconstruction network. In this work, we used an unrolled reconstruction network similar to 10,11 that mimic the proximal gradient based solutions for compressed sensing. Our overall network architecture is illustrated in Figure 1.
Using the variational bound on mutual information, we can express our objective as $$\mathcal{L}(\phi, \theta;\mathcal{D})=\max_{\phi,\theta}\sum_{x\in\mathcal{D}}E_{q_\phi(Z|x)}[\log{p_\theta(x|z)}]$$ This formulation allows optimizing k-space sample coordinates $$$(\phi)$$$ and reconstruction network parameters $$$(\theta)$$$ using backpropagation. In this framework, we optimize $$$\phi$$$ and $$$\theta$$$ for the entire dataset as opposed to having separate acquisition and reconstruction parameters for each example in the dataset. At test time, the learned sampling pattern is fixed and reconstruction is done using the learned reconstruction network.
Results
We used the "Stanford Fully-Sampled 3D FSE Knees" dataset available in mridata.org12 which contains 3D knee scans from 20 subjects acquired with 8 channels. The sensitivity maps were estimated using ESPIRiT13. Each of the slices were treated as separate examples during training and validation.In our experiments, we consider the 3D acquisition case where we optimize the phase encoding locations in 2D k-space. We considered four acceleration factors: R=5, 10, 15, 20. For each acceleration factor, we initialized the k-space sampling pattern $$$(\phi)$$$ using Variable Density Sampling (VDS)14, and picked $$$\sigma=0.001$$$ for the measurement noise $$$\epsilon$$$. We then ran our model and compared the result with the case where we only optimized the reconstruction network.
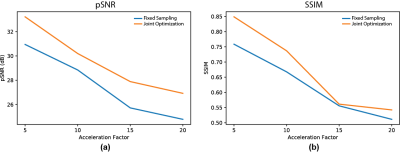
Figure 2 shows pSNR and SSIM metric results for the proposed joint optimization framework and the VDS baseline. We observe that joint optimization using our framework improves reconstruction quality as indicated by the 1.4-2.2dB increase in pSNR.
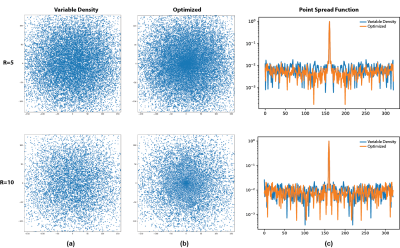
Figure 3 shows the initial and optimized sampling patterns along with the point spread function (PSF) of the sampling pattern before and after optimization. Sampling optimization accumulates more samples near k-space center and reduces the gaps between them. The sidelobes of the PSF are suppressed which reduces the amount of aliasing due to undersampling.
Figure 4 shows the reconstruction results on a sample test slice for $$$R=5$$$ and $$$R=10$$$. Sampling optimization using our framework enhances reconstruction quality. In addition, zero-filling reconstruction using the optimized samples have less severe aliasing artifacts, making it easier for the decoder network to remove these artifacts.
Conclusion and Discussion
This work explores the use of variational information maximization and deep uncertainty autoencoders for learning the sampling pattern in MRI jointly with image reconstruction. Using the nuFFT operator in the encoder enables continuous optimization of k-space sample coordinates. On a knee MR dataset, we have shown that the optimized sampling pattern improves reconstruction quality, highlighting possible benefits that can be obtained by learning undersampling patterns.One observation is that the peripheral samples do not change as much as the samples near origin during training. Incorporating additional regularizers that emphasize high frequency information can improve the gradient flow to these samples.
Our framework allows incorporating other MR physics related artifacts beyond the Gaussian measurement noise such as motion and off-resonance effects. These artifacts can be simulated as a part of the forward model to find the optimal sampling locations in the presence of such effects.
Acknowledgements
This work is supported by NIH R01EB009690 and R01EB026136, as well as GE Healthcare.References
1. Kyong Hwan Jin, Michael Unser, and Kwang Moo Yi. Self-supervised deep active accelerated mri. arXiv preprint arXiv:1901.04547, 2019.
2. Zizhao Zhang, Adriana Romero, Matthew J Muckley, Pascal Vincent, Lin Yang, and Michal Drozdzal. Reducing uncertainty in undersampled mri reconstruction with active acquisition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 2049–2058, 2019.
3. Luis Pineda, Sumana Basu, Adriana Romero, Roberto Calandra, and Michal Drozdzal. Active mr k-space sampling with reinforcement learning. arXiv preprint arXiv:2007.10469, 2020.
4. Cagla Deniz Bahadir, Adrian V Dalca, and Mert R Sabuncu. Learning-based optimization of the under-sampling pattern in mri. In International Conference on Information Processing in Medical Imaging, pages 780–792. Springer, 2019.
5. Iris AM Huijben, Bastiaan S Veeling, and Ruud JG van Sloun. Learning sampling and model-based signal recovery for compressed sensing mri. In ICASSP 2020-2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), pages 8906–8910. IEEE, 2020.
6. Hemant Kumar Aggarwal and Mathews Jacob. J-modl: joint model-based deep learning for optimized sampling and reconstruction. IEEE Journal of Selected Topics in Signal Processing,14(6):1151–1162, 2020.
7. Tomer Weiss, Ortal Senouf, Sanketh Vedula, Oleg Michailovich, Michael Zibulevsky, and Alex Bronstein. Pilot: Physics-informed learned optimal trajectories for accelerated mri. arXiv preprint arXiv:1909.05773, 2019.
8. Aditya Grover and Stefano Ermon. Uncertainty autoencoders: Learning compressed representations via variational information maximization. In The 22nd International Conference on Artificial Intelligence and Statistics, pages 2514–2524, 2019.
9. Ralph Linsker. How to generate ordered maps by maximizing the mutual information between input and output signals. Neural computation, 1(3):402–411, 1989.
10. Joseph Y Cheng, Feiyu Chen, Marcus T Alley, John M Pauly, and Shreyas S Vasanawala. Highly scalable image reconstruction using deep neural networks with bandpass filtering. arXiv preprint arXiv:1805.03300, 2018.
11. Christopher M Sandino, Joseph Y Cheng, Feiyu Chen, Morteza Mardani, John M Pauly, and Shreyas S Vasanawala. Compressed sensing: From research to clinical practice with deep neural networks: Shortening scan times for magnetic resonance imaging. IEEE Signal Processing Magazine, 37(1):117–127, 2020.
12. F Ong, S Amin, SS Vasanawala, and M Lustig. An open archive for sharing mri raw data. In ISMRM & ESMRMB Joint Annual Meeting, page 3425, 2018.
13. Martin Uecker, Peng Lai, Mark J Murphy, Patrick Virtue, Michael Elad, John M Pauly, Shreyas S Vasanawala, and Michael Lustig. Espirit—an eigenvalue approach to autocalibrating parallel mri: where sense meets grappa. Magnetic resonance in medicine, 71(3):990–1001, 2014.
14. Michael Lustig, David Donoho, and John M Pauly. Sparse mri: The application of compressed sensing for rapid mr imaging. Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine, 58(6):1182–1195, 2007.
Figures