0228
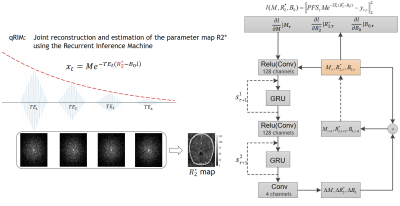
A unified model for simultaneous reconstruction and R2* mapping of accelerated 7T data using the Recurrent Inference Machine1Biomedical Engineering & Physics, Amsterdam UMC, Amsterdam, Netherlands, 2Biomedical Imaging Group Rotterdam, Erasmus MC, Rotterdam, Netherlands, 3Radiology, Amsterdam UMC, Amsterdam, Netherlands, 4Integrative Model-based Cognitive Neuroscience research unit, University of Amsterdam, Amsterdam, Netherlands, 5Max Planck Institute for Human Cognitive and Brain Sciences, Leipzig, Germany
Synopsis
Quantitative MRI often relies on the acquisition of multiple images with different scan settings. Therefore, data redundancy can be exploited to further accelerate imaging by deep learning. We propose a unified model for joint reconstruction and $$$R_2^*$$$-mapping from sparse data and embed this in a Recurrent Inference Machine, an iterative inverse problem solving network. Applied to high-resolution multi-echo gradient echo data of a cohort study covering the entire adult life span, the error in $$$R_2^*$$$ significantly decreases. With increasing acceleration factor, an increasing reduction in error is observed, pointing to a larger benefit for sparser data.
Introduction
$$$R_2^*$$$-mapping finds its application in image-guided Deep Brain Stimulation for Parkinson's disease, and detection of hemorrhage, micro-calcifications and iron deposits1. $$$R_2^*$$$ is typically computed voxel-wise from fitting a relaxation model to reconstructed multi-echo gradient echo (ME-GRE) images. Long acquisition times associated with such scans can be reduced by deep learning in MR image reconstruction on subsampled k-space data. However, if data redundancy over multi-echo data is not exploited, possible image blur may be introduced and larger errors seen in estimated parameter maps. To accelerate beyond what is possible with volume-wise reconstruction alone we propose to unify the image reconstruction and relaxation models. By adopting the recurrent inference machine (RIM) for image reconstruction2, and formulating a unified forward model, we reconstruct and fit an $$$R_2^*$$$-map to subsampled k-spaces directly. We perform experiments in high-resolution 7T data and aim to reduce the error in the estimated $$$R_2^*$$$-maps.Methods
For quantitative MRI (qMRI) multiple images are acquired in the same subject with different scan specifications. Specifically, for $$$R_2^*$$$-estimation with a ME-GRE sequence, images of multiple echoes are acquired, and the measured image intensity $$$\mathbf{x_t}$$$ at echo time $$$TE_t$$$ follows from this forward relaxation model:$$\mathbf{x_t}=Me^{-TE_t (R_2^*-B_0 i)}+\eta_t$$
Here M is the net magnetization, $$$B_0$$$ is the static magnetic field, and $$$\eta_t$$$ is the noise of echo $$$t$$$. Following the image reconstruction model with a multi-channel receive coil, the measured k-space signal of echo t and coil channel c is computed as
$$\mathbf{y_{t,c}}=P(FS_c \mathbf{x_t} + \eta_{t})$$ where $$$S_c$$$ is the sensitivity map of coil channel c, F is the Fourier transform, P is the subsampling mask of the k-space. By merging these equations, we unify the image reconstruction and relaxation model as
$$\mathbf{y_{t,c}}=P(FS_c Me^{-TE_t (R_2^*-B_0 i)} + \eta_{t})$$.
With the unified model we aim to estimate the parameter $$$R_2^*$$$ along with M and $$$B_0$$$ from k-space by training a recurrent inference machine (RIM)2:
$$ \hat{\theta} = \mathrm{argmax}_\theta \mathrm{SSIM} \left( A_\theta (M_{init},R_{2,init}^*,B_{0,init}),(M,R_2^*,B_0) \right) $$
where $$$A_\theta$$$ is the function of the RIM parameterized by $$$\theta$$$ to predict the parameters from an initial estimation of the parameters $$$M_{init},R_{2,init}^*,B_{0,init}$$$, and the k-space measurements $$$\mathbf{y}$$$. T is the number of time steps. As a method to solve the inverse problem, the RIM estimates the parameters from the perspective of maximum a posteriori (MAP) estimation, maximizing the sum of the log-likelihood and log-prior distributions:
$$ M,R_2^*,B_0 = \mathrm{argmax}_{M,R_2^*,B_0} \left( \mathrm{log} p(y|M,R_2^*,B_0) + \mathrm{log} p(M,R_2^*,B_0) \right) $$
The negative log-likelihood can be expressed as data consistency between the measured k-space $$$y$$$ and the predicted $$$\hat{y}$$$ (see Fig. 1). In our neural network, the log-prior of the parameters $$$\theta$$$ is implicit and learned from the training data. The architecture of the model is visualized in Fig. 1. The RIM iteratively updates the parameter estimation for the next time step with the current estimation and a hidden state, and the additional gradient of the log-likelihood.
Experiments
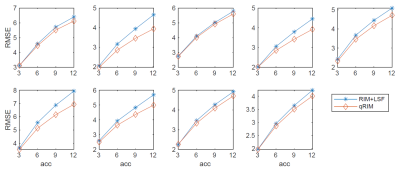
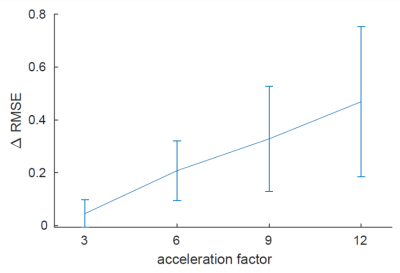
Data were selected from the AHEAD database, covering the adult life span3. The MP2RAGE-ME sequence with FatNav motion navigators4 was used on a Philips 7T scanner, with a resolution of 0.7mm, two-fold accelerated along one phase-encoding dimension. For $$$R_2^*$$$-mapping, the multi-echo second inversion data was GRAPPA-interpolated and motion-corrected, after which k-space training data was obtained by Fourier-transforming individual coil images.To validate the proposed method, we trained and tested the RIMs with retrospectively subsampled k-spaces in 2D. The subsampling was with Gaussian pseudo-random patterns with acceleration factors of 3 to 12 with a fraction of 0.02 fully sampled in the k-space center. Subsampling patterns varied per TE. 17 training, 2 validation, and 10 testing subjects were used, respectively. As a preprocessing step for initializing the parameter maps, a RIM model for image reconstruction was used, and least squares fitting (LSF) was performed. The ground-truth maps were fitted by LSF on fully sampled data. The comparison was made between the prediction of the proposed method (qRIM) and the initialized maps, i.e., results of RIM-reconstruction+LSF (RIM+LSF). The Root Mean Squared Error (RMSE) was computed for all testing subjects, and the difference between the reference and proposed method ΔRMSE was statistically tested to be different from zero using an unpaired t-test and to increase with acceleration factor using linear regression.
Results and Discussion
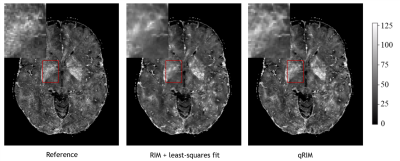
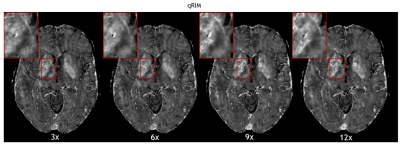
The RMSE for all testing subjects is shown in Fig. 2, and mean and standard deviation of ΔRMSE for all acceleration factors is shown in Fig. 3. The results show that the RMSE of the proposed model is reduced compared to the RIM-LSF results in all subjects. ΔRMSE was significantly larger than zero, even for 3-fold acceleration (p=0.03), and the reduction increases with acceleration factor (p<1e-5). Fig. 4 shows a predicted slice from one testing subject. Compared to the RIM+LSF, the prediction of RIM-qMRI shows a sharper image with more detailed image contents preserved. Fig. 5 shows that image quality is largely preserved, also for high acceleration factors, at the cost of modest blur.Conclusion
The proposed qRIM using a unified forward model for reconstruction and parameter estimation is able to exploit the redundancy among TEs thanks to the ended forward model. This allowed to reduce RMSE while showing improved image sharpness, illustrating the added value of unified modeling.Acknowledgements
No acknowledgement found.References
1 Stüber, C., Morawski, M., Schäfer, A., Labadie, C., Wähnert, M., Leuze, C., Streicher, M., Barapatre, N., Reimann, K., Geyer, S., Spemann, D., & Turner, R. (2014). Myelin and iron concentration in the human brain: a quantitative study of MRI contrast. NeuroImage, 93 Pt 1, 95–106.
2 Lønning, K., Putzky, P., Sonke, J.-J., Reneman, L., Caan, M. W. A., & Welling, M. (2019). Recurrent inference machines for reconstructing heterogeneous MRI data. Medical Image Analysis, 53, 64–78. https://doi.org/10.1016/j.media.2019.01.005
3 Alkemade, A., Mulder, M. J., Groot, J. M., Isaacs, B. R., van Berendonk, N., Lute, N., Isherwood, S. J., Bazin, P.-L., & Forstmann, B. U. (2020). The Amsterdam Ultra-high field adult lifespan database (AHEAD): A freely available multimodal 7 Tesla submillimeter magnetic resonance imaging database. NeuroImage, 117200.
4 Caan, M. W. A., Bazin, P. L., Marques, J. P., de Hollander, G., Dumoulin, S. O., & van der Zwaag, W. (2019). MP2RAGEME: T1, T2*, and QSM mapping in one sequence at 7 tesla. Human Brain Mapping, 40(6), 1786–1798.
Figures