Introduction

In recent years, several methods have been proposed that used deep learning algorithms in an MR image reconstruction for fast MRI^1-6. Most of the current deep-learning-based MR reconstruction methods used the coil sensitivity maps that were pre-computed by coil sensitivity estimation methods such as ESPIRiT method⁷. However, with a high reduction factor or with fewer ACS lines of acquired k-space data, estimated coil sensitivity maps may not be accurate and could affect the reconstruction performance of MR images⁸. In this study, we propose a Joint Deep Model-based MR Image and Coil Sensitivity Reconstruction Network (Joint-ICNet) that jointly reconstructs an MR image and coil sensitivity maps from undersampled multi-coil k-space data using deep learning networks and interleaved MR model-based data consistency schemes.

Methods

Problem Formulation: The purpose of this study is to reconstruct an MR image from undersampled multi-channel k-space data using deep-learning networks. Thus, the objective function can be formulated as the following least squares equation:
$$\min_{\mathbf{x},\mathbf{C}}\left\Vert{\mathbf{Ax-b}}\right\Vert^2_2+\lambda_I\left\Vert{\mathbf{x}-\mathcal{D}_I(\mathbf{x})}\right\Vert^2_2+\lambda_F\left\Vert{\mathbf{x}-\mathcal{F}^{-1}\mathcal{D}_F(\mathbf{f})}\right\Vert^2_2+\lambda_C\left\Vert{\mathbf{C}-\mathcal{D}_C(\mathcal{F}^{-1}\mathbf{b})}\right\Vert^2_2,$$
where $$$\mathbf{x}$$$ denotes the desired MR image, $$$\mathbf{b}$$$ denotes the measured multi-coil k-space data, $$$\mathbf{A}$$$ denotes the forward operator that has a coil sensitivity map $$$\mathbf{C}$$$ , Fourier transform $$$\mathcal{F}$$$, and a k-space sampling matrix $$$\mathbf{M}$$$, $$$\mathcal{D}_I$$$ is the de-aliasing model that reconstructs artifacts-free MR images from $$$\mathbf{x}$$$, $$$\mathcal{D}_F$$$ is the k-space model that interpolates missing k-space data points from $$$\mathbf{f}$$$, $$$\mathbf{f}$$$ represents the k-space of $$$\mathbf{x}$$$ that is Fourier transformed by $$$\mathcal{F}$$$, $$$\mathcal{D}_C$$$ is the coil sensitivity model that estimates coil sensitivity maps from the acquired k-space data $$$\mathbf{b}$$$, $$$\lambda_I$$$, $$$\lambda_F$$$, and $$$\lambda_C$$$ represent the regularization parameters of $$$\mathcal{D}_I$$$, $$$\mathcal{D}_F$$$, and $$$\mathcal{D}_C$$$, respectively. The least squares problem of the equation can be solved sequentially using a gradient descent method with an iterative algorithm in terms of $$$\mathbf{x}$$$ and $$$\mathbf{C}$$$, respectively, as
$$\begin{cases}\mathbf{x}_{k+1}=\mathbf{x}_k-2\mu_k\left[\mathbf{A}^*(\mathbf{A}\mathbf{x}_k-\mathbf{b})+\lambda_k^I(\mathbf{x}_k-\mathcal{D}_I(\mathbf{x}_k))+\lambda_k^F(\mathbf{x}_k-\mathcal{F}^{-1}\mathcal{D}_F(\mathbf{f}))\right],\\\mathbf{C}_{k+1}=\mathbf{C}_k-2\nu_k\left[\mathbf{x}_k^*\mathcal{F}^{-1}\mathbf{M}^\top(\mathbf{A}\mathbf{x}_k-\mathbf{b})+\lambda_k^C(\mathbf{C}_k-\mathcal{D}_C(\mathcal{F}^{-1}\mathbf{b}))\right],\end{cases}$$
where $$$\mu_k$$$ and $$$\nu_k$$$ are the step size of $$$\mathbf{x}_k$$$ and $$$\mathbf{C}_k$$$ at iteration $$$k$$$ $$$(k = 0, … , N_k)$$$, respectively, and $$$N_k$$$ represents the number of iterations. $$$\mathbf{x}_k$$$ and $$$\mathbf{C}_k$$$ are sequentially reconstructed from above equations.

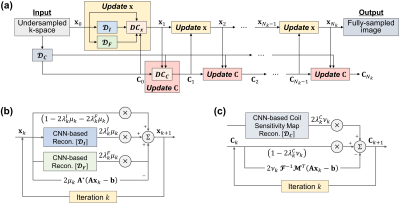
Proposed Model: The detailed architecture of Joint-ICNet is presented in Fig. 1 and Fig. 2. Joint-ICNet consists of two main blocks: 1) an MR image reconstruction block that reconstructs an MR image from undersampled multi-coil k-space data with convolutional neural network (CNN)-based regularizations and a model-based data consistency layer of an MR image, and 2) a coil sensitivity maps reconstruction block that estimates coil sensitivity maps from undersampled k-space data with a CNN-based regularization and a model-based data consistency layer of coil sensitivity maps. The desired MR image and coil sensitivity maps can be obtained by sequentially estimating them with two blocks.

Implementation Details: We used U-net⁹ based architectures for the CNN-based regularizations $$$\mathcal{D}_I$$$, $$$\mathcal{D}_F$$$, and $$$\mathcal{D}_C$$$, where U-net has four pooling and up-sampling layers. Each convolutional block located in U-net consisted of a 2D convolutional layer followed by a leaky rectified linear unit (leaky ReLU) with 0.2 negative slope coefficient and instance normalization. The trainable parameters of regularization $$$\lambda_k$$$, and step sizes $$$\mu_k$$$ and $$$\nu_k$$$ were initialized as 1. A total of 10 iterations (i.e., $$$N_k=10$$$) was performed in the unrolled network. The Joint-ICNet was trained with a structural similarity (SSIM) loss function¹⁰.

Experiments: We used multi-coil k-space data of the fastMRI open dataset¹¹. The dataset has brain MRI scans including T1 weighted, T1 weighted with contrast agent (T1POST), T2 weighted, and FLAIR images taken from various vendors. During the training, 20% of the slices were used for the training and the validation, which were randomly selected from the dataset. For the test, the whole test slices were used. The k-space data were retrospectively undersampled using 1D Cartesian equispaced sampling masks. The reduction factors were R = 4 and 8. Three metrics including a normalized root mean squared error (NRMSE), a peak signal-to-noise ratio (PSNR), and SSIM were used to quantitatively evaluate the reconstructed images.

Results

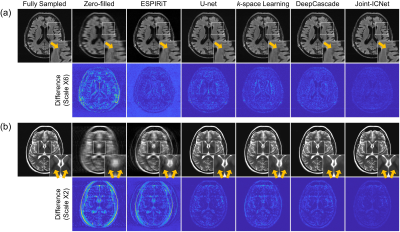
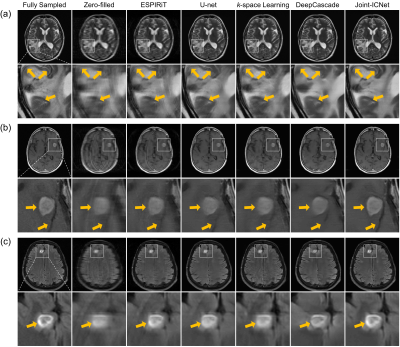
We compared Joint-ICNet with a conventional PI-based method, ESPIRiT⁷, and deep-learning-based MR reconstruction methods, which were U-net⁹, k-space learning², and DeepCascade⁵. Fig. 3 presents the fully sampled and reconstructed (a) FLAIR images with the reduction factor R = 4, and (b) T2 images with the reduction factor R = 8, respectively. Compared to other methods, Joint-ICNet shows superior performance in reconstructing images and removing artifacts as shown on the magnified and difference images. The reconstructed results with abnormal cases are shown in Fig. 4, which presents fully sampled and reconstructed (a) T2, (b) T1POST, and (c) FLAIR images, with the reduction factor R = 4. Whereas the conventional PI-based and other deep-learning-based methods could not recover the blurred abnormal tissues, Joint-ICNet recovered those similar to the fully sampled images, as shown on the magnified images. In addition, Joint-ICNet had the lowest NRMSE, and the highest PSNR and SSIM values compared to other reconstruction methods, as presented in Table 1.

Conclusion

We proposed a joint deep model-based MR image and coil sensitivity reconstruction network, called Joint-ICNet, that jointly reconstructs an MR image and coil sensitivity maps from undersampled multi-coil k-space data. Experiments with various MR images and reduction factors demonstrated that our proposed Joint-ICNet showed superior performance compared to conventional PI-based and state-of-the-art deep-learning-based reconstruction methods in reconstructing the MR images.

Acknowledgements

This research was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Science and ICT (2019R1A2B5B01070488) and Y-BASE R&E Institute a Brain Korea 21, Yonsei University.