0223
Motion-resolved B1+ prediction using deep learning for real-time pTx pulse-design.1Cardiff University Brain Research Imaging Centre, Cardiff, United Kingdom
Synopsis
Motion in parallel-transmit (pTx) causes flip-angle error due to dependence of channels' B1-sensitivities on head position. Real-time pTx pulse-design could mitigate motion-induced flip-angle error, but requires real-time, motion-resolved B1+ distributions (not measurable). A deep learning method is presented to estimate motion-resolved B1+ maps via a system of conditional generative adversarial networks. Using simulations, we demonstrate that estimated maps can be used to design tailored pTx pulses which yield similar flip-angle profiles to those without motion, reducing maximum observed flip-angle error from 79% to 25%. Importantly, networks can be run sequentially to accurately predict B1+ for arbitrary displacements incorporating multiple directions.
Introduction
Parallel-transmission (pTx) of pulses can overcome B1 nonuniformity at 7T1-3, however individual channels’ fields and interference patterns depend on the coil load (position, composition, geometry)4-5. As a result, flip-angle and specific absorption rate (SAR) distributions are sensitive to motion in pTx, leading to image quality and safety concerns6-9. Retrospective motion correction is therefore inadequate. Conservatively-bounded SAR estimates are used, but prevent optimal imaging performance3,10.Real-time pTx pulse-design is a feasible solution11-12, but requires real-time B1+ distributions (not measurable). Data not directly measurable by MR (eg. tissue conductivity) can be predicted by conditional generative adversarial networks (cGANs), given some MR-accessible data as input13-15. Neural networks have been used to predict (non-pTx) B1+ from localizers at 7T for slice-dependent pulse scaling to reduce SAR, however prediction quality was head position dependent16.
Here, we use simulations and train cGANs to predict pTx B1+ distributions (henceforth B1-maps) following head motion, given one initial B1-map. If used with motion detection17-18, this permits motion-resolved B1-estimation (and therefore real-time pulse re-design). Flip-angle and SAR distributions of (SAR-unconstrained) pTx pulses designed using network-predicted B1-maps are compared to those using the conventional approach of designing pulses from the initial B1-map alone.
Methods
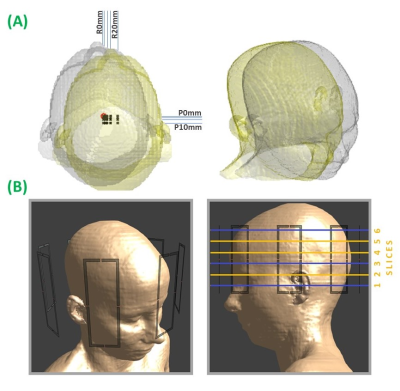
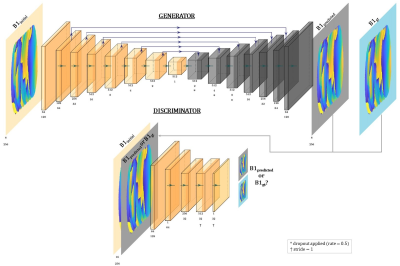
Billie, Duke and Ella body models (IT’IS, Zurich, Switzerland)19 were simulated at 295MHz with an 8-channel pTx coil in Sim4Life (ZMT, Zurich, Switzerland). In [7], axial displacements had the largest local-SAR effects, therefore each model was simulated at one central, and 19 off-centre positions on the axial plane (figure 1). Other simulation details followed those in [7].Network architecture (figure 2) is adapted from [20]. The Adam21 optimizer (learning rate= 2e-4) was used to train models in TensorFlow for 60 epochs. Separate networks were trained for large (5mm) and small (2mm) displacements in rightward (R) and posterior (P) directions, yielding a total of 8 networks (4 magnitude, 4 phase).
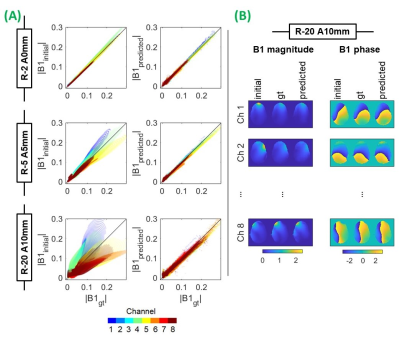
Data were input to networks as 2-D (256x256) slices of B1-map, with corresponding slices before (input) and after (ground-truth) a given displacement as input-target pairs. Networks were validated with the Billie data (excluded during training) at all off-centre positions, and 6 slice locations (figure 1). All available relative displacements were included in training and evaluation (ie. the initial position was not always the origin), meaning networks’ training dataset size depended on the number of simulated positions fulfilling a relative displacement. This yielded between 408 and 600 unique input-target slice pairs. Where necessary networks were cascaded; using the output of one network as input to the next sequentially (eg. R5mm, R5mm, P2mm networks were cascaded for evaluation at R10 P2mm position).
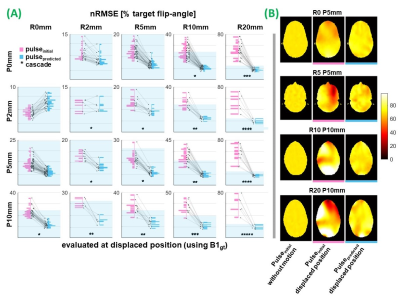
Corresponding magnitude and phase network outputs were combined to form complex predicted maps (B1predicted). 5-spoke pTx pulses were designed using an adaptation of [22-23]. 1-spoke (RF-shim) pulses were also designed for SAR evaluation. For each evaluation, a conventional pulse (pulseinitial) was first designed using the initial position’s B1-map (B1initial) for uniform in-plane excitation. A second pulse (pulsepredicted) was designed using network-output B1predicted (proposed approach). Both pulses were subsequently evaluated at the corresponding ground-truth displaced position (B1gt) to quantify motion-induced effects, and improvement provided by the proposed approach. Their flip-angle distributions were compared with that of pulseinitial without motion via root-mean-squared-error (nRMSE), normalised by target flip-angle (70°). Peak local-SAR (psSAR) of both pulses was also evaluated using 10-g averaged Q-matrices24.
Results and Discussion
Figure 3 shows that the proposed approach reduced excitation profile error in 91% of evaluations. Motion caused nRMSE of 79% in the worst-case, which was reduced to 25% by re-designing pulses using B1predicted. Maximum observed motion-induced phase error was 0.2 radians lower for pulsepredicted. Largest error reductions were seen for larger displacements and/or inferior slice locations where motion-induced error was highest, however pulsepredicted performance was largely independent of displacement magnitude.Voxelwise correlations show that, beyond the smallest movements, B1predicted resembled B1gt more so than B1initial, including where models were cascaded multiple times (figure 4). Even for small displacements, motion-induced error is systematically channel and motion-direction dependent. Residual error in B1predicted is spatially random in comparison, therefore does not accumulate when channels are superposed, and thereby avoids regions of very high or low flip-angle when pulses are applied to B1gt. Residual network error becomes comparable to motion-induced error when the latter is low, (ie. smaller displacements), but the benefit of the proposed method is clear for larger displacements; common among certain patient populations25-26. Comprehensive network optimization was beyond the scope of this initial investigation but is expected to further improve network prediction quality.
Following motion, psSAR was lower for pulsepredicted than pulseinitial in 82% and 62% of 5-spoke and RF-shimming evaluations, respectively (figure 5). The method does not guarantee SAR reduction (psSAR of pulsepredicted was higher for some displacements and slice locations), since these observations arise incidentally due to compensation of motion-induced B1 changes, and pulses were not SAR-constrained.
Conclusions
Motion-resolved B1-maps can be estimated online using cGANs. These maps can be used for pseudo real-time pTx pulse-design11-12. Maximum motion-induced flip-angle nRMSE was reduced from 79% to 25% with the re-designed pulses. Importantly, networks can be run sequentially to predict B1-distributions following arbitrary displacements comprising multiple directions. Here, error was reduced for 18 displacements using networks trained for just 4 displacements.Acknowledgements
No acknowledgement found.References
[1] J. Vaughan, et al., 7T vs. 4T: RF power, homogeneity, and signal-to-noise comparison in head images. Mag Res Med,64 (1), pp. 24–30, 2001.
[2] U. Katscher and P. Bornert, Parallel RF transmission in MRI. NMR Biomed,19 (3), pp. 393–400, 2006.
[3] C. M. Deniz, Parallel transmission for ultrahigh field MRI. Topics in Mag Res Imag,28 (3), pp. 159–171, 2019.
[4] U. Katscher, et al., Basic considerations on the impact of the coil array on the performance of transmit sense. Mag Res Mat Phys Biol Med, 18 (2), pp. 81–88, 2005.
[5] C. M. Deniz, et al., Radiofrequency energy deposition and radiofrequency power requirements in parallel transmission with increasing distance from the coil to the sample. Mag Res Med, 75 (1), pp. 423–432, 2016.
[6] E. Kopanoglu, et al. Implications of within-scan patient head motion on B1+ homogeneity and specific absorption rate at 7T. Proc. Intl. Soc. Mag. Reson. Med. 27, 2019.
[7] E. Kopanoglu, et al., Specific absorption rate implications of within-scan patient head motion for ultra-high field MRI. Mag Res Med, 2020.
[8] S. Wolf, et al., SAR simulations for high-field MRI: How much detail, effort, and accuracy is needed? Mag Res Med, 69 (4), pp. 1157–1168, 2013.
[9] N. Schon, et al., Impact of respiration on B1+ field and SAR distribution at 7T using a novel EM simulation setup. Proc. Intl. Soc. Mag. Reson. Med., 28, 2020.
[10] E. F. Meliado, et al., Conditional safety margins for less conservative peak local SAR assessment: A probabilistic approach. Mag Res Med, 2020.
[11] E. Kopanoglu, Near real-time parallel-transmit pulse design. Proc. Intl. Soc. Mag. Reson. Med., 26, 2018.
[12] E. Kopanoglu and R. T. Constable, Radiofrequency pulse design using nonlinear gradient magnetic fields. Mag Res Med, 74 (3), pp. 826–839, 2015.
[13] S. Mandija, et al., Opening a new window on MR-based electrical properties tomography with deep learning. Scientific Reports, 9 (1), 2019.
[14] S. Bollmann, et al., “DeepQSM - using deep learning to solve the dipole inversion for quantitative susceptibility mapping. NeuroImage, 195, pp. 373–383, 2019.
[15] E. Meliado et al., A deep learning method for image-based subject-specific local SAR assessment. Mag Res Med, 83 (2), pp. 695–711, 2020.
[16] S. Abbasi-Rad, et al., Improving FLAIR SAR efficiency at 7T by adaptive tailoring of adiabatic pulse power through deep learning B1+ estimation. Mag Res Med, 2020.
[17] J. Maclaren, et al., Prospective motion correction in brain imaging: A review. Mag Res Med, 69 (3), pp. 621–636, 2013.
[18] P. Digiacomo, et al., “A within-coil optical prospective motion-correction system for brain imaging at 7T. Mag Res Med, 2020.
[19] M-C. Gosselin, et al., Development of a new generation of high-resolution anatomical models for medical device evaluation: The virtual population 3.0. Phys Med Bio, 59 (18), pp. 5287–5303, 2014.
[20] P. Isola, et al., Image-to-image translation with conditional adversarial networks, 2018. arXiv:1611.07004.
[21] D. Kingma and J. Lei Ba, Adam: A method for stochastic optimization. Proceedings of the Conference on Learning Representations, 2015.
[22] Grissom, W.et al. Spatial domain method for the design of RF pulses in multicoil parallel excitation. Magnetic Resonance in Medicine, 56, 620–629, 2006.
[23] ISMRM RF Pulse-design Challenge. http://challenge.ismrm.org/. 2016.
[24] I. Graesslin, et al., A specific absorption rate prediction concept for parallel transmission MR. Mag Res Med, 68 (5), pp. 1664–1674, 2012.
[25] K. T. Chen, et al., MR-assisted PET motion correction in simultaneous PET/MRI studies of dementia subjects. JMRI, 2018.
[26] S. Kecskemeti, et al., Robust motion correction strategy for structural MRI in unsedated children demonstrated with three-dimensional radial MPNRAGE. Radiology, 289 (2), pp. 509–516,2018.
Figures