0222
Subtle Inverse Crimes: Naively using Publicly Available Images Could Make Reconstruction Results Seem Misleadingly Better!1Electrical Engineering and Computer Sciences, UC Berkeley, Berkeley, CA, United States, 2Electrical and Computer Engineering, The University of Texas at Austin, Austin, TX, United States
Synopsis
This work reveals how naively using publicly available data for training and evaluating reconstruction algorithms may lead to artificially improved algorithm performance. We observed such practice in the “wild” and aim to bring this to the attention of the community. The underlying cause is common data preprocessing pipelines which are often ignored: k-space zero-padding in clinical scanners and JPEG compression in database storage. We show that retrospective subsampling of such preprocessed data leads to overly-optimistic reconstructions. We demonstrate this phenomenon for Compressed-Sensing, Dictionary-Learning and Deep Neural Networks. This work hence highlights the importance of careful task-adequate usage of public databases.
Introduction
Modern advanced and learning-based MRI reconstruction algorithms are often developed using images from public databases. Several databases are specifically designed for MRI reconstruction and provide raw k-space data1,2, while many others offer images, often as magnitude and in DICOM or NIfTI format, originally intended for other tasks3-5 (i.e. segmentation or biomarker discovery). Due to their availability, the latter are often used by researchers for reconstruction purposes; however, this may lead to artificially-improved results. Using magnitude over complex data is an obvious advantage, but there are additional subtle and often ignored image-processing pipelines that further artificially bias the reconstructions. Here we demonstrate how two common data preprocessing pipelines related to commercial MRI scanners and DICOM data can artificially improve the results of algorithms based on Compressed Sensing (CS)6, Dictionary Learning (DL)7 and Deep Neural Network (DNN)8. We show that in a typical algorithm evaluation experiment, which involves retrospective subsampling of k-space data, the hidden preprocessing pipelines yield improved algorithm performance. We hence coin the term subtle inverse crimes to describe the misleading evaluation of inverse problem solvers on unsuitable preprocessed data9.Conceptual Framework
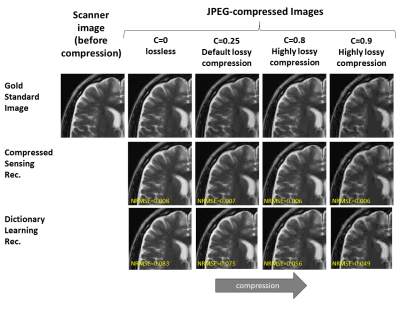
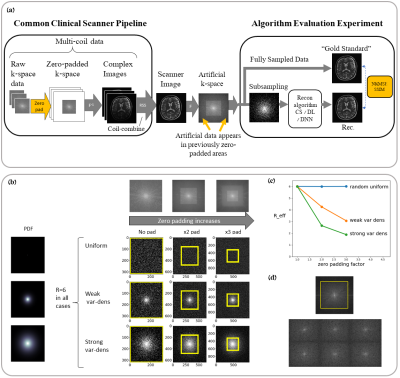
Subtle Crime I: Zero-padding. Commercial scanners often interpolate images by zero-padding k-space, performing an inverse DFT, and applying a subsequent coil combination, for example by a Root Sum of Squares (RSS) (Figure 1a). The zero-padding step is extremely common and often applied by default in commercial scanners; magnitude image databases hence often include zero-padded data. The zero-padding squashes the “true” k-space data to the center; therefore, when a retrospective variable-density subsampling scheme is applied, the “true” data is sampled with a higher effective density (Figure 1b,c). The inverse problem therefore becomes easier to solve and algorithms may exhibit artificially improved performance. To demonstrate this, we study how image quality metrics, NRMSE and SSIM, are affected by the zero-padding and subsequent variable density sampling.Subtle Crime II: JPEG compression. Lossy JPEG compression is sometimes part of the DICOM pipeline10 or database storage. The JPEG-compressed image is then used as the ground truth for a retrospective experiment (Figure 2). This “ground truth” compressed data has lower entropy than typical MR data, therefore retrospective experiments leveraging image spatial redundancy benefit from the compression.
Methods
Algorithms. We study three reconstruction algorithms:1. CS with l1-wavelet regularization6, implemented using SigPy11 with $$$λ=0.005$$$.
2. A Dictionary Learning method that jointly solves for the dictionary and the sparse code using alternating minimization4. The method was implemented using an open-source code12 with Orthogonal Matching Pursuit13 for the sparse code recovery and K-SVD14 for the dictionary update.
3. Unrolled DNN: The MoDL algorithm8 was implemented in PyTorch15 with a U-Net16, 6 unrolls, 8 CG steps, l1-loss and the Adam optimizer17.
Data & implementation. Experiments were performed on MR images from the FastMRI database2 (unprocessed raw data), with 531 (87) train (test) images from 35 subjects. To demonstrate the subtle crimes in a variety of cases, CS and DL were implemented on brain data with 2D subsampling while MoDL was implemented on knee data with 1D (full columns) subsampling.
The standard JPEG implementation of the PILLOW Library18 was used. We performed a set of experiments with various JPEG compression factors. We defined $$$c=(100-q)/100$$$ as a measure of the compression strength, where $$$q$$$ is the JPEG compression quality, and studied a range of $$$q$$$ values: 100 (lossless), 75 (default lossy compression), 50 (mildly lossy) and 10-20 (highly lossy). Different datasets were created for each $$$q$$$ value, and the models were trained on them separately.
Results
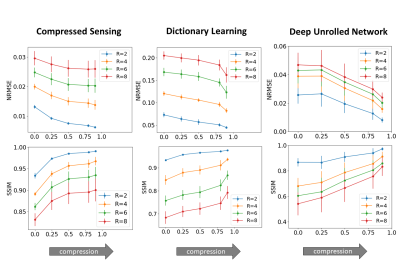
Subtle Crime I. Figure 3a demonstrates the zero-padding effect: high zero-padding together with retrospective dense sampling leads to a clear improvement in the reconstruction quality, both visually and in terms of NRMSE. Since the reconstruction algorithm parameters were identical in all experiments, this improvement is artificial; it results only from the preprocessing and retrospective subsampling. This effect is further demonstrated in a set of experiments (Figure 3b): CS, DL and DNNs all exhibit an artificial improvement in a similar scenario.Subtle Crime II. To demonstrate how using JPEG-compressed data affects retrospective experiments we studied a range of compression values. Figure 4 demonstrates the JPEG paradoxical effect: the higher the compression, the lower the NRMSE even though the visual image quality degrades. This occurs because the NRMSE is measured against a “gold standard” compressed image. Importantly, although the default compression is visually unnoticeable, it still artificially reduces the NRMSE by about 10%, as demonstrated for both CS and DL. Moreover, Figure 5 shows that all the studied algorithms (CS, DL and DNN) are sensitive to the JPEG subtle crime.
Discussion and Conclusion
This work highlights a subtle and often ignored phenomenon: training and evaluation of reconstruction algorithms on preprocessed data may lead to artificially improved results. Our experiments reveal that CS, DL and DNN algorithms may all exhibit overly-optimistic performance due to subtle data preprocessing. One possible remedy strategy is to crop zero-padded k-space areas; another is to avoid retrospective subsampling of magnitude preprocessed data. Public datasets are extremely useful, yet not all are suitable for all purposes; this work emphasizes the importance of careful data usage and detection of inadequate pipelines by researchers and reviewers.Acknowledgements
The authors acknowledge funding from grants U24 EB029240-01, R01EB009690, 01HL136965.References
1. Ong, F., Amin, S., Vasanawala, S., & Lustig, M. (2018). Mridata. org: An open archive for sharing MRI raw data. In Proc. Intl. Soc. Mag. Reson. Med (Vol. 26, p. 1).
2. Zbontar, J., Knoll, F., Sriram, A., Murrell, T., Huang, Z., Muckley, M. J., ... & Parente, M. (2018). FastMRI: An open dataset and benchmarks for accelerated MRI. arXiv preprint arXiv:1811.08839.
3. IXI database. Resources for the computational analysis of brain development, Imperial College, http://biomedic.doc.ic.ac.uk/brain-development.
4. The Human Connectome Project, University of Souterhn California, http://www.humanconnectomeproject.org/publications/documents/.
5. Mueller, S. G., Weiner, M. W., Thal, L. J., Petersen, R. C., Jack, C. R., Jagust, W., ... & Beckett, L. (2005). Ways toward an early diagnosis in Alzheimer’s disease: the Alzheimer’s Disease Neuroimaging Initiative (ADNI). Alzheimer's & Dementia, 1(1), 55-66.
6. Lustig, M., Donoho, D., & Pauly, J. M. (2007). Sparse MRI: The application of compressed sensing for rapid MR imaging. Magnetic Resonance in Medicine: 58(6), 1182-1195.
7. Ravishankar, S., & Bresler, Y. (2010). MR image reconstruction from highly undersampled k-space data by dictionary learning. IEEE transactions on medical imaging, 30(5), 1028-1041.
8. Aggarwal, H. K., Mani, M. P., & Jacob, M. (2018). MoDL: Model-based deep learning architecture for inverse problems. IEEE transactions on medical imaging, 38(2), 394-405.
9. Guerquin-Kern, M., Lejeune, L., Pruessmann, K. P., & Unser, M. (2011). Realistic analytical phantoms for parallel magnetic resonance imaging. IEEE Transactions on Medical Imaging, 31(3), 626-636.
10. Herrmann, M. D., Clunie, D. A., Fedorov, A., Doyle, S. W., Pieper, S., Klepeis, V., ... & Kikinis, R. (2018). Implementing the DICOM standard for digital pathology. Journal of pathology informatics, 9.
11. Ong, F., & Lustig, M. (2019). SigPy: a python package for high performance iterative reconstruction. In Proceedings of the ISMRM 27th Annual Meeting, Montreal, Quebec, Canada (abstract 4819).
12. Tamir, J. (2020). Step-by-Step Reconstruction Using Learned Dictionaries. In: Proceedings of the ISMRM 28th Annual Meeting, (Virtual Meeting).
13. Pati, Y. C., Rezaiifar, R., & Krishnaprasad, P. S. (1993). Orthogonal matching pursuit: Recursive function approximation with applications to wavelet decomposition. In Proceedings of 27th Asilomar conference on signals, systems and computers (pp. 40-44). IEEE.
14. Aharon, M., Elad, M., & Bruckstein, A. (2006). K-SVD: An algorithm for designing overcomplete dictionaries for sparse representation. IEEE Transactions on signal processing, 54(11), 4311-4322.
15. Paszke, A., Gross, S., Massa, F., Lerer, A., Bradbury, J., Chanan, G., ... & Desmaison, A. (2019). Pytorch: An imperative style, high-performance deep learning library. In Advances in neural information processing systems (pp. 8026-8037).
16. Ronneberger, O., Fischer, P., & Brox, T. (2015). U-net: Convolutional networks for biomedical image segmentation. In International Conference on Medical image computing and computer-assisted intervention (pp. 234-241). Springer, Cham.
18. Kingma, D. P., & Ba, J. (2014). Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980.
19. Clark, A. (2015). Pillow (PIL Fork) https://pillow.readthedocs.io/en/stable/.
Figures
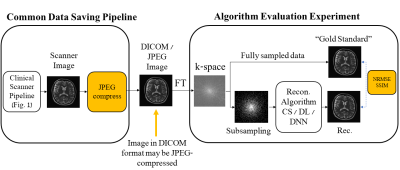
Subtle Crime II concept. MR images are often saved in the DICOM format which sometimes involves JPEG compression. However, JPEG-compressed images contain less high-frequency data than the original data; therefore, algorithms trained on retrospectively-subsampled compressed data may benefit from the compression. These algorithms may hence exhibit misleadingly good performance.