0221
On Instabilities of Conventional Multi-Coil MRI Reconstruction To Small Adversarial Perturbations1Electrical and Computer Engineering, University of Minnesota, Minneapolis, MN, United States, 2Center for Magnetic Resonance Research, University of Minnesota, Minneapolis, MN, United States, 3University of Florida, Gainesville, FL, United States, 4MIT-IBM Watson AI Lab, IBM Research, Cambridge, MA, United States
Synopsis
Although deep learning (DL) has received much attention in accelerated MRI, recent studies suggest small perturbations may lead to instabilities in DL-based reconstructions, leading to concern for their clinical application. However, these works focus on single-coil acquisitions, which is not practical. We investigate instabilities caused by small adversarial attacks for multi-coil acquisitions. Our results suggest that, parallel imaging and multi-coil CS exhibit considerable instabilities against small adversarial perturbations.
Introduction
Deep learning (DL) reconstruction has recently received much attention due to its improved reconstruction quality1-5. While DL has been transformative in many image processing tasks, it is well-understood that these methods may be susceptible to instabilities arising from small adversarial perturbations due to their non-linear nature6-8. Such instabilities were also explored for MRI reconstruction recently9, which suggested that both researchers and FDA need to be cognizant of these issues. Several follow-up studies10,11 explored adversarial training frameworks to improve the robustness of DL-MRI reconstruction. However, all these works concentrated on a single-coil setup, which has little practical application.In this work, we investigate how small adversarial perturbations affect multi-coil MRI reconstruction, particularly using conventional non-DL methods. Our results indicate that for multi-coil MRI reconstruction, parallel imaging and multi-coil compressed sensing (CS) methods are also susceptible to large instabilities from small adversarial perturbations.
Methods
Multi-coil MRI Acquisition Model and Inverse Problem: The multi-coil encoding model is given as: $$\textbf{y$_\Omega$}=\textbf{E$_\Omega$x}+\textbf{n}\tag{1}$$ where $$$\textbf{y$_\Omega$}$$$ is the acquired measurements with sub-sampling pattern $$$\textbf{$\Omega$}$$$, $$$\textbf{E$_\Omega$}$$$ is the multi-coil encoding matrix, and $$$\textbf{n}$$$ is noise. For i.i.d. Gaussian noise, the maximum likelihood estimate is $$\mathrm{arg}\min\limits_{x}||\textbf{y$_\Omega$}-\textbf{E$_\Omega$x}||_2^2=(\textbf{E$^\textit{H}_\Omega$}\textbf{E$_\Omega$})^{-1}\textbf{E$^\textit{H}_\Omega$}\textbf{y$_\Omega$}\tag{2}$$ which is the CG-SENSE12 output without regularization. Alternatively, a regularized version of the problem can be solved $$\mathrm{arg}\min \limits_{x}||\textbf{y$_\Omega$}-\textbf{E$_\Omega$x}||_2^2+\mathcal{R}(\textbf{x})\tag{3}$$ where $$$\mathcal{R}(\textbf{$\cdot$})$$$ is a regularizer, e.g. Tikhonov or l1-norm of transform coefficients. In DL methods that rely on algorithm unrolling5, the regularizer is implicitly learned through neural networks, leading to a non-linear representation.Adversarial Attacks: Let $$$\textbf{z} = \textbf{E$^\textit{H}_\Omega$}\textbf{y$_\Omega$}$$$ denote the zero-filled image, and $$$\textit{f}(\textbf{z$_{\Omega}$})$$$ be a reconstruction algorithm that takes as input the zero-filled image. Note that while the reconstruction algorithm may take $$$\textbf{y$_\Omega$}$$$ as input, using the zero-filled image allows consistency with the setup in9. We use an l∞-attack, i.e. the attack $$$\textbf{r}$$$ on the input with $$$||\textbf{r}||_{\infty}<\epsilon$$$ leads to a reconstruction $$$\textit{f}(\textbf{z$_{\Omega}$}+\textbf{r})$$$ that largely deviates from the original output $$$\textit{f}(\textbf{z$_{\Omega}$})$$$. The attack is chosen on the zero-filled image instead of the fully-sampled image as done in9, because the latter is not practical: 1) One does not have access to fully-sampled images to generate a practical attack, 2) In multi-coil MRI, the encoding operator is not known exactly, but estimated. Finally, the attack is not chosen in k-space, since it is difficult to define an l∞-perturbation in k-space due to the varying signal strength between center and edges.
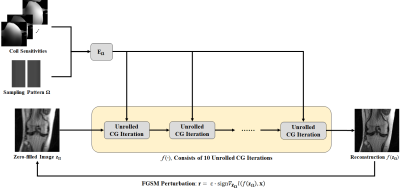
Imaging Data and Experiments: Coronal proton density knee MRI with 15-channel coils were obtained from the fastMRI database13. An acceleration rate, R = 4 with 24 ACS lines was used, as common in DL-MRI reconstruction14. Both uniform and random undersampling were investigated. For the former, CG-SENSE and GRAPPA were considered, while for the latter, CG-SENSE and multi-coil CS were explored. For both undersampling patterns, the attacks were performed on the CG-SENSE solution. Specifically, the CG algorithm was unrolled for 10 iterations3. The attack was generated on this unrolled CG using fast gradient sign method15 with an MSE loss and $$$\epsilon=||\textbf{r}||_{\infty}/255$$$ (Fig. 1). For random undersampling, this attack was used directly on multi-coil CS. For uniform undersampling, the small perturbation attack on the zero-filled image was converted to k-space for GRAPPA. Among the infinitely many k-space perturbations on $$$\textbf{$\Omega$}$$$ that led to $$$\textbf{r}$$$ , the minimum l2 solution was picked.
For testing, CG-SENSE used 10 iterations; GRAPPA used 5×4 kernels. Multi-coil CS reconstruction utilized variable splitting, l1-norm of Daubechies4 wavelets as the regularizer, and its parameters were tuned empirically. All coil maps were generated using ESPIRiT16.
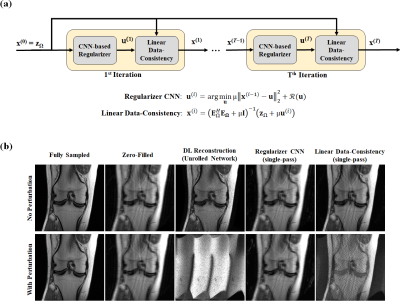
Additionally, an attack was generated on a pre-trained DL method17,18 based on an unrolled network to investigate whether the linear data- consistency units or the non-linear neural networks used for regularization were affected more substantially.
Results
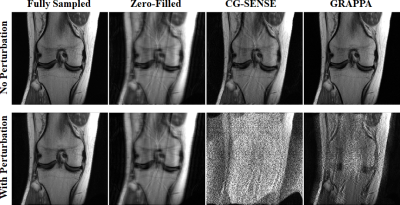
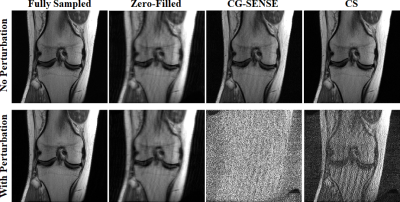
Fig. 2 depicts CG-SENSE and GRAPPA results for uniform undersampling. While the perturbation causes no visual difference in the fully-sampled image, both methods fail under the attack. Fig. 3 shows CG-SENSE and multi-coil CS reconstructions for random undersampling. The same conclusions apply, with both methods failing under a non-visible small perturbation.Fig. 4 depicts the results of an unrolled neural network under an attack that targets it end-to-end. There is no major change when the attack is run through a single regularizer unit, but output collapses when the attack is passed through a single data-consistency unit. This suggests the end-to-end attack on an unrolled network targets the linear data-consistency units.
Discussion and Conclusions
Our results indicate that for multi-coil MRI reconstruction, parallel imaging and multi-coil CS are also susceptible to large instabilities from small adversarial perturbations. Moreover, for DL reconstruction that utilize $$$\textbf{E$_\Omega$}$$$ explicitly, adversarial attacks predominantly target the linear data consistency units. The ill-conditioning of the encoding operator is well-discussed for CG-SENSE in non-Cartesian acquisitions, which has led to an early stopping criterion in practice19. While in general, it is hard to compute the condition number, which depends on the coil configuration and R, adversarial attacks enable a method to exploit such ill-conditioning. Since these attacks also breakdown multi-coil MRI reconstruction methods, including parallel imaging and CS, it is worthwhile to interpret the instabilities of DL methods within this broader context.Acknowledgements
The first three authors contributed equally to this work. Grant support: NIH R01HL153146, NIH P41EB027061, NIH U01EB025144; NSF CAREER CCF-1651825References
1. Wang S, Su Z, Ying L, et al. Accelerating magnetic resonance imaging via deep learning. IEEE 13th International Symposium on Biomedical Imaging (ISBI); 2016; 514-517.
2. Hammernik K, Klatzer T, Kobler E, et al. Learning a variational network for reconstruction of accelerated MRI data. Magn Reson Med. 2018; 79(6):3055-3071.
3. Aggarwal HK, Mani MP, Jacob M. MoDL: Model-Based Deep Learning Architecture for Inverse Problems. IEEE Trans Med Imaging. 2019; 38(2):394-405.
4. Schlemper J, Caballero J, Hajnal JV, et al. A Deep Cascade of Convolutional Neural Networks for Dynamic MR Image Reconstruction. IEEE Transactions on Medical Imaging. 2018; 37(2): 491-503. doi:10.1109/tmi.2017.2760978.
5. Knoll F, Hammernik K, Zhang C, et al. Deep Learning Methods for Parallel Magnetic Resonance Image Reconstruction. IEEE Signal Processing Magazine. 2020; 37(1):128-140.
6. Moosavi-Dezfooli SM, Fawzi A, Frossard P. Deepfool: A simple and accurate method to fool deep neural networks. Proc. IEEE Conference on Computer Vision and Pattern Recognition. 2016; 2574-2582.
7. Moosavi-Dezfooli SM, Fawzi A, Fawzi O, et al. Universal adversarial perturbations. Proc. IEEE Conference on Computer Vision and Pattern Recognition. 2017; 86–94.
8. Szegedy C, Zaremba W, Sutskever I, et al. Intriguing properties of neural networks. Proc. International Conference on Learning Representations. https://openreview.net/forum?id=kklr_MTHMRQjG. Accessed 28 April 2020.
9. Antun V, Renna F, Poon C. On instabilities of deep learning in image reconstruction and the potential costs of AI. Proc. PNAS. 2020; 117(48):30088–30095.
10. Raj A, Bresler Y, Li B. Improving Robustness of Deep-Learning-Based Image Reconstruction. arXiv preprint. 2020; arXiv:2002.11821.
11. Genzel M, Macdonald J, März M. Solving Inverse Problems With Deep Neural Networks--Robustness Included? arXiv preprint. 2020; arXiv:2011.04268.
12. Pruessmann KP, Weiger M, Börnert P, et al. Advances in Sensitivity Encoding With Arbitrary k-Space Trajectories, Magn Reson Med. 46:638–651.
13. Knoll F, Zbontar J, Sriram A, et al. fastMRI: A Publicly Available Raw k-Space and DICOM Dataset of Knee Images for Accelerated MR Image Reconstruction Using Machine Learning. Radiology: Artificial Intelligence. 2020; 2(1): e190007.
14. Knoll F, Murrell T, Sriram A, et al. Advancing machine learning for MR image reconstruction with an open competition: Overview of the 2019 fastMRI challenge. Magn Reson Med. 2020; 84:3054–3070.
15. Goodfellow IJ, Shlens J, Szegedy C. Explaining and Harnessing Adversarial Examples. arXiv preprint. 2014; arXiv:1412.6572.
16. Uecker M, Lai P, Murphy M J, et al. ESPIRiT—an eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA. Magn Reson Med. 2014; 71(3):990-1001.
17. Yaman B, Hosseini SAH, Moeller S, et al. Self-supervised learning of physics-guided reconstruction neural networks without fully sampled reference data. Magn Reson Med. 2020; 84:3172–3191.
18. Hosseini SAH, Yaman B, Moeller S, et al. Dense recurrent neural networks for accelerated MRI: History-cognizant unrolling of optimization algorithms. IEEE J Selec Top Sign Proc. 2020; 14(6):1280-1291.
19. Maier O, Baete SH, Fyrdahl A, et al. CG-SENSE revisited: Results from the first ISMRM reproducibility challenge. arXiv preprint. 2020; arXiv:2008.04308.
Figures