0212
3t++ temporally consistent 3 tissue HARDI decomposition of neonatal brain tissue1Forensic & Neurodevelopmental Sciences, King's College London, London, United Kingdom, 2Centre for the Developing Brain, School of Biomedical Engineering and Imaging Sciences, King’s College London, Kings Health Partners, St. Thomas Hospital, London, SE1 7EH, UK, King's College London, London, United Kingdom, 3Department of Electrical Engineering (ESAT/PSI), KU Leuven, Leuven, Belgium, 4Biomedical Engineering Department, School of Biomedical Engineering and Imaging Sciences, King's College London, London, United Kingdom, 5Department of Perinatal Imaging & Health, School of Biomedical Engineering and Imaging Sciences, King's College London, London, United Kingdom, 6MRC Centre for Neurodevelopmental Disorders, King's College London, London, United Kingdom
Synopsis
We decompose neonatal HARDI signal into four components that together capture the orientation dependency and temporal dependency of signal in neonatal white and grey matter and CSF. We show that the voxel-wise volume fractions of the associated components exhibit distinct sigmoid-shaped time dependencies between 33 to 44 weeks gestational age and clearly delineate anatomical structures in developing white and grey matter, allowing detailed characterisation of microstructural properties of developing white and grey matter.
Introduction
In adults, multi-shell multi-tissue constrained spherical deconvolution (MSMT-CSD)1 applied to High Angular Resolution Diffusion Imaging (HARDI) data allows characterising CSF, white matter (WM) and cortical grey matter (GM) tissue properties using a set of tissue-specific signal signatures “response functions” that capture their respective b-value and angular properties.In the neonatal period, brain parenchyma exhibits age-dependent b-value and angular properties, reflecting cell composition, density, and water content. In previous work, this was modelled as a non-negative combination of signal fingerprints from CSF and WM single-fibre regions sampled at the age-extremes2.
In this study, we extend this work to derive more biologically plausible canonical response functions that are constrained to yield temporally consistent decompositions of neonatal brain tissue across gestational ages. To do this, we replace the convexity constraint used in previous work1-3 with the constraint that component fractions across all tissue types should sum to one for all time points in the cohort.
Methods
We used HARDI data from 108 neonates included in the developing Human Connectome Project (dHCP)2, scanned between 33.4 and 44.6 weeks postmenstrual age (wPMA) ($$$b = 0, 0.4, 1$$$ and $$$2.6 ms / \mu m^2$$$ with $$$n=20, 64, 88$$$ and $$$128$$$ directions respectively)4,5. These were processed using complex-domain denoising6, EPI distortion correction using FSL topup7, motion correction using a multi-shell data representation with outlier suppression8, inter-slice intensity inhomogeneity correction9, and transformation to the extended dHCP T2w-atlas space10 using rigid co-registration of dMRI and T2w images with FSL flirt11.In all subjects, initial responses were estimated from CSF, single-fibre WM and isotropic GM-like voxels, selected using the dhollander heuristic12, followed by consensus filtering to harmonise the WM response selection (minimum agreement: 2 subjects) and intensity normalisation using mtnormalise13. The coefficients of all of these responses were then concatenated into the matrix $$$X\in\mathbb{R}^{n\,\times\,m}$$$ with $$$m=24$$$ coefficients (6 per shell) and $$$n=3\times108$$$ tissue- and subject-specific response functions.
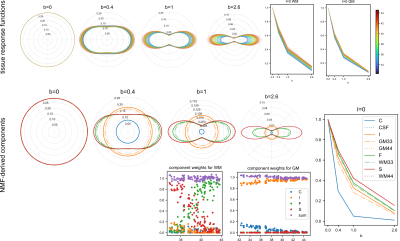
This matrix $$$X$$$ was decomposed into $$$r=4$$$ canonical components using semi-nonnegative matrix factorisation (sNMF), which minimises the objective $$$\frac{1}{2}\|X-WH\|_F\text{, s.t. } W_{ij} \geq 0 \forall i,j$$$ for the weight and coefficient matrices $$$W\in\mathbb{R}^{n\,\times\,r}_{+}$$$ and $$$H\in\mathbb{R}^{r\,\times\,m}$$$ by alternating updates to $$$H$$$ and $$$W$$$. We initialise the sNMF model via convexity-constrained NMF14 and introduce constraints in the subsequent sNMF optimisation:
a) row-wise normalisation of the weights $$$W$$$ to sum to 1,
b) ten iterations of unconstrained updates to $$$H$$$ and $$$W$$$,
c) zeroing of l>0 components in $$$H$$$ that are smaller than 5% of the 95th percentile absolute coefficient in $$$X$$$ in the corresponding angular band.
Steps a-c are repeated for 1000 iterations.
Finally, the four resulting canonical response functions and corresponding ODFs produced by MSMT-CSD were scaled such that the angular mean of the ODFs sum to one (on average) across all brains in the cohort using mtnormalise.
Results & discussion
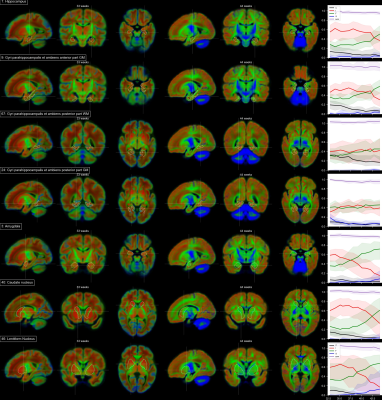
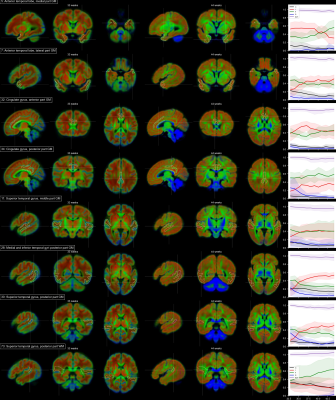
Voxels selected as single-fibre WM and isotropic adult GM-like show a clear age dependency (Fig 1). The sNMF components model WM responses as a linear transition from a fast-decaying anisotropic component F (similar to WM at 33 wPMA) to a slow-decaying anisotropic component S (similar to WM at 44 wPMA). The WM responses in the youngest group also contain up to 20% of the isotropic (dot) component I (similar to GM at 44 wPMA). The responses in GM are modelled as a combination of free fluid (C) and isotropic component (I) with a linear reduction of C over time.In WM, we observe a transition from F to S in inferior-to-superior and posterior-to-anterior direction (Figs 2,3). The earliest transitioning WM regions are located in the cerebellum, brainstem, corticospinal tract and the corona radiata extending into the motor cortex, capturing expected WM maturation patterns.
Cortical tissue in the youngest group contains a small degree of radially oriented signal associated with S (see Figs 2, 5) in-line with fetal data15, possibly related to transient glial and neuronal scaffolding.
In cortical GM in the temporal gyri, I increases with age (Fig 5), resembling more adult-like GM over time. In the ventrolateral thalamus (Fig.3.42), insular GM (Fig3.20), amygdala (Fig.4.3), caudate and lentiform nucleus (Fig.4.40,46), F increases while I decreases. Similarly, in the rest of the thalamus (Fig.3.86) and subthalamic nuclei (Fig.3.44), I decreases with age though with a marked increase in S and decrease of F starting at about 35 wPMA. This is consistent with early maturation of the subthalamic nucleus that starts to myelinate before 29 weeks and continues to myelinate beyond 37 wPMA16.
Conclusion
We present a data-driven method for decomposing neonatal HARDI fingerprints that capture properties of CSF, WM and isotropic GM-like signal using a set of canonical components. These provide a compelling basis to study brain development, with consistent developmental trajectories within, and distinct profiles between, known cortical, subcortical GM and WM regions.Acknowledgements
This work was supported by ERC grant agreement no. 319456 (dHCP project), the Wellcome EPSRC Centre for Medical Engineering at Kings College London (WT 203148/Z/16/Z) and by the National Institute for Health Research (NIHR) Biomedical Research Centre based at Guy’s and St Thomas’ NHS Foundation Trust and King’s College London. DC is supported by the Flemish Research Foundation (FWO; grant number 12ZV420N). JH is funded by a UKRI FLF [MR/T018119/1]. MP is funded in part by the Bill & Melinda Gates Foundation (INV-005774). JOM is supported by a Sir Henry Dale Fellowship jointly funded by the Wellcome Trust and the Royal Society (Grant Number 206675/Z/17/Z). The views expressed are those of the authors and not necessarily those of the NHS, the NIHR or the Department of Health.References
1. Jeurissen, B., Tournier, J.-D. D., Dhollander, T., Connelly, A. & Sijbers, J. Multi-tissue constrained spherical deconvolution for improved analysis of multi-shell diffusion MRI data. NeuroImage 103, 411–426 (2014).
2. Pietsch, M. et al. A framework for multi-component analysis of diffusion MRI data over the neonatal period. NeuroImage (2018) doi:10.1016/j.neuroimage.2018.10.060.
3. Christiaens, D., Maes, F., Sunaert, S. & Suetens, P. Convex Non-Negative Spherical Factorization of Multi-Shell Diffusion-Weighted Images. vol. 9349 (Springer International Publishing, 2015).
4. Hutter, J. et al. Time-efficient and flexible design of optimised multi-shell HARDI diffusion. (2017) doi:10.1002/mrm.26765.
5. Tournier, J. et al. A data‐driven approach to optimising the encoding for multi‐shell diffusion MRI with application to neonatal imaging. NMR Biomed. 33, (2020).
6. Cordero-Grande, L., Christiaens, D., Hutter, J., Price, A. N. & Hajnal, J. V. Complex diffusion-weighted image estimation via matrix recovery under general noise models. NeuroImage 200, 391–404 (2019).
7. Andersson, J. L. R., Skare, S. & Ashburner, J. How to correct susceptibility distortions in spin-echo echo-planar images: application to diffusion tensor imaging. NeuroImage 20, 870–888 (2003).
8. Christiaens, D. et al. Scattered slice SHARD reconstruction for motion correction in multi-shell diffusion MRI. NeuroImage 225, 117437 (2021).
9. Pietsch, M., Christiaens, D., Hajnal, J. V. & Tournier, J.-D. dStripe: slice artefact correction in diffusion MRI via constrained neural network. bioRxiv (2020).
10. Schuh, A. et al. Unbiased construction of a temporally consistent morphological atlas of neonatal brain development. http://biorxiv.org/lookup/doi/10.1101/251512 (2018).
11. Jenkinson, M. & Smith, S. A global optimisation method for robust affine registration of brain images. Med. Image Anal. 5, 143–156 (2001).
12. Dhollander, T., Mito, R., Raffelt, D. & Connelly, A. Improved white matter response function estimation for 3-tissue constrained spherical deconvolution. in Proc Intl Soc Mag Reson Med 555 (2019).
13. Raffelt, D. et al. Bias Field Correction and Intensity Normalisation for Quantitative Analysis of Apparent Fibre Density. in Proc. Intl. Soc. Mag. Reson. Med. vol. 25 3541 (2017).
14. Ding, C., Li, T. & Jordan, M. I. Convex and semi-nonnegative matrix factorizations. IEEE Trans. Pattern Anal. Mach. Intell. 32, 45–55 (2010).
15. Pietsch, M. et al. Multi-component atlas of fetal brain development via decomposition of diffusion MRI. in ISMRM vol. 28 77 (2020).
16. Counsell, S. J. et al. MR imaging assessment of myelination in the very preterm brain. Am. J. Neuroradiol. 23, 872–881 (2002).
Figures
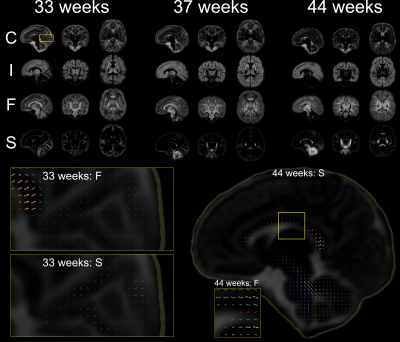
Top: Volume fraction maps of the four components at 33, 37 and 44 wPMA. The bottom part shows component C overlaid with ODFs of components F and S. Bottom left: magnified areas highlighting the splenium of the corpus callosum and cortical areas with radial organisation. Bottom right: separation of the late-maturing cingulum captured by component F and body of the corpus callosum, captured in component S at 44 wPMA.