Introduction

MR Fingerprinting (MRF) is a quantitative imaging method that simultaneously provides multiple tissue property maps¹. Appropriate pulse sequences can reduce scan time with improved measurement precision. However, such an optimization problem is very challenging. It is nontrivial and computationally expensive to model both spatially and temporally dependent acquisition errors and random errors in the objective function. To address these issues, here we propose an advanced MRF optimization framework that 1) uses a fast computing strategy to model spatially and temporally dependent artifacts due to systematic errors including undersampling and phase errors, and 2) directly minimizes the resulting quantitative errors in the simulated tissue property maps in the cost function. A quantum-inspired optimization (QIO) approach, which has been shown to be able to escape from local minima, is adopted to handle this optimization problem with minimal constraints.

Methods

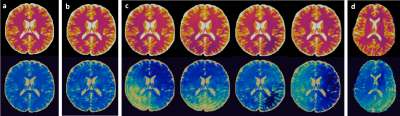
Cost Function definition
While the proposed framework could be applied to any MR sequence, we have started with an MRF-FISP sequence². The cost function was constructed as a weighted combination of T1 and T2 errors due to random noise and systematic errors with a scan time penalty. The measure of random error was inferred in terms of quality factors that estimates the likelihood of signal errors due to thermal noise³. The systematic errors include aliasing artifacts due to undersampling and phase errors due to system imperfections such as B0 inhomogeneity. They are the dominant error sources in fast MRF scans, and the interplay between the two results in commonly seen shading artifacts in in vivo MRF maps (Figure 1.d). Accurately predicting these spatially and temporally dependent artifacts is a key to evaluate sequence performance during optimization and provide fast and robust MRF scans. The systematic errors were estimated using a fast image series simulator⁴, where a three-tissue digital brain phantom was used to simulate highly undersampled images imposed with additional phase errors to obtain the aliased MRF maps (Figure 1.c). This simulator alone achieved a factor of over 100 accelerations in computing MRF images as compared to a conventional NUFFT method.
Optimization
480 flip angles and 480 TR variables were separately parameterized as a function of 20 pulse indexes using cubic splines. Optimizations were carried out by substochastic Monte Carlo⁵, a quantum inspired optimization algorithm, and simulated annealing method⁶ to find a global optimum.
Validation
We first evaluated the image quality of the optimized scans in simulations. The fully sampled images of a brain phantom were first simulated using the ground truth signal evolutions. Spatially dependent phase maps with four different directional variations were simulated, and multiplied to the fully sampled images to model the phase errors. The images were then undersampled with a single shot spiral in k-space per TR. Finally, the undersampled images were reconstructed into T1 and T2 MRF maps via dictionary matching (Figure 1.c).
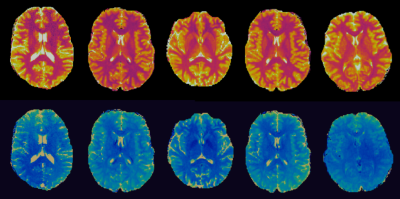
The optimized sequences were validated by multiple in vivo scans to evaluate image quality and reproducibility. In vivo scans were performed on healthy volunteers in compliance with the IRB in a Siemens 3T Skyra scanner. All scans were acquired with an image resolution of 1.2×1.2 mm² using a spiral acquisition, with an undersampling factor of 48.
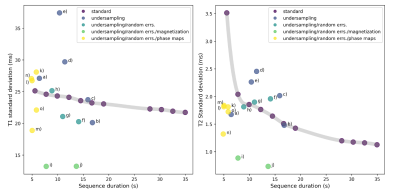
Reproducibility of the optimized MRF sequences against random errors were evaluated via bootstrapping simulations⁷ using in vivo data. The results were compared against the performance of the human-designed MRF sequence, where the sequence was truncated to different durations to obtain a tradeoff relation between its precision and duration.

Results

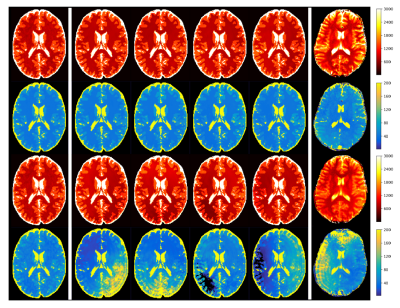
Figure 1 shows the simulation results of a MRF sequence using different simulation methods. The simulated maps obtained by incorporating both undersampling and phase errors show shading artifacts similar to those in in vivo scans, which supports this simulation method as replicating in vivo conditions.
Figure 2 shows the simulation results of an example optimized sequence. In the simulation, maps from the human-designed sequence are subject to severe shading artifacts; whereas the optimized scan is immune to such artifacts. In vivo performance (Figure 3) of several optimized scans show similar results, which validates their robustness against undersampling and system variations.
Figure 4 shows the bootstrap statistics of optimized sequences generated from various cost functions in comparison with human-designed sequences. The optimizer can yield sequences achieving higher precision at given duration or shorter length for comparable precision. Note that bootstrap simulations only estimate random errors but not undersampling errors and phase errors, thus the optimized sequences that behaves the best in bootstrapping exams may not be the ones exhibiting the best image quality.
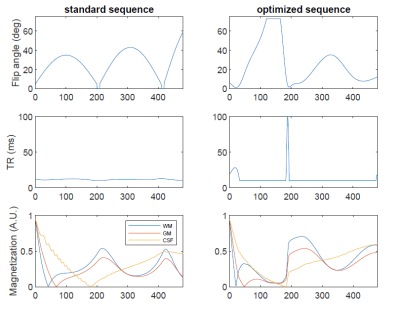
Figure 5 shows an optimized sequence pattern. It illustrates very distinct pattern features that are consistently observed in optimized sequences, such as “saturated” flip angles and “spiked” TR values at low flip angle regions.

Conclusion

We propose an optimization framework to automatically design MRF scans to achieve increased precision and intrinsic robustness against undersampling artifacts and system imperfections. This optimization paradigm facilitates great flexibility in cost function design. Therefore, it could be extended for more complex MRF implementations, or modified for different MRF applications.

Acknowledgements

The authors would like to acknowledge funding from Siemens Healthineers, Microsoft and NIH grant EB026764-01 and NS109439-01