Introduction

Magnetization transfer contrast MR fingerprinting (MTC-MRF) is a novel quantitative imaging method that simultaneously quantifies free bulk water and semisolid macromolecule parameters using pseudo-randomized scan parameters^1-2. However, the quantification accuracy is highly dependent on the MRF sequence because of its extensive range of capabilities for encoding the pertinent information. Thus, the optimization of MRF sequence has been of recent interest in the MRF field^3-5, but has been challenging due to a large number of degrees of freedom in the sequence. Most of the current methods are based on indirect measurements, such as maximizing the signal difference between different tissue parameters, or maximizing the signal-to-noise ratio (SNR) efficiency using the constrained Cramer-Rao lower bound (CRLB). However, the optimized MRF schedule through the aforementioned indirect metrics cannot guarantee the low quantification errors for each tissue parameter. In this study, we propose a framework for learning-based optimization of the acquisition schedule (LOAS), which optimizes RF saturation-encoded MRF acquisitions with a minimum number of dynamic scans for tissue parameter determination. Particularly, LOAS updates scan parameters to minimize a loss function that directly represents tissue quantification errors in a supervised manner.

Method

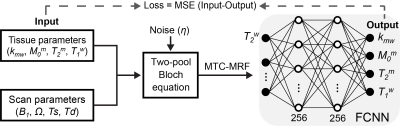
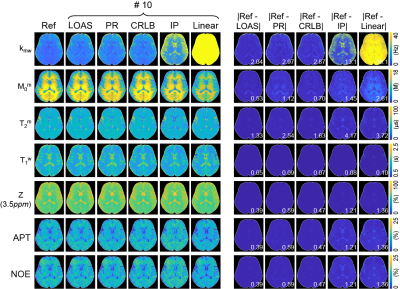
A fully-connected neural network (FCNN) incorporated with two-pool Bloch equation was designed to optimize the acquisition schedule for tissue parameter quantification. MTC-MRF signal profiles were generated using randomly initialized scan parameters and tissue parameters through an analytical solution of two-pool Bloch equation. The FCNN takes the simulated MTC-MRF signals as an input and outputs parameter estimates (Fig. 1). The loss function was a mean square difference between the ground-truth (Input) and the estimated tissue parameters (Output). The scan parameters were updated to minimize the loss via the adaptive moment estimation (ADAM) optimizer, hence decreasing quantification errors through epochs. The proposed method was validated using simulated digital phantoms and in vivo experiments, and compared with other sub-optimal MTC-MRF schedules (CRLB, Interior-point (IP), Pseudo-random (PR), Linear). A synthetic technique in lieu was performed to validate the LOAS method on in vivo data. The tissue parameter maps estimated using deep-learning FCNN-based quantification method with the PR schedule (forty dynamic scans) were defined as the reference (namely, Reference) and used to generate synthetic 3D MTC-MRF images via the two-pool Bloch equation. Synthetic 3D MTC-MRF images with various MRF schedules were used for the deep-learning FCNN based quantification method. The resultant water and MTC quantitative maps were compared to the reference tissue maps. For in-vivo studies, six healthy volunteers (mean age: 36 years; range 27 to 41 years of age) were scanned on a 3T MRI scanner after written, informed consent was obtained, in accordance with the IRB requirements. In addition, amide proton transfer (APT) and nuclear Overhauser enhancement (NOE) images with RF saturation power of 1.2 μT were calculated by subtracting synthesized MTC images (Z_ref) from B₀-corrected, experimentally measured images (Z_lab) at ±3.5 ppm, respectively (Z = S_sat/S₀, where S_sat and S₀ are the signal intensities measured with and without RF saturation, respectively).

Result and Discussion

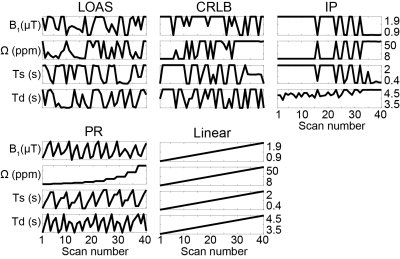
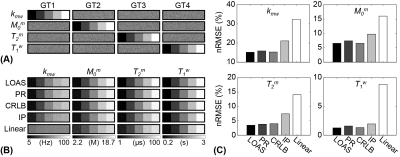
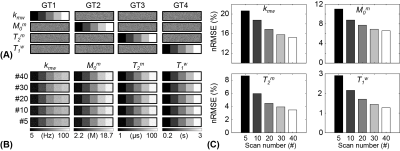
The acquisition schedules optimized by LOAS, CRLB, and IP strategies, and PR and Linear schedules are shown in Fig. 2. Optimized MRF schedules were evaluated using digital phantoms encoded by the two-pool transient-state MTC model. Water and MTC parameters estimated from the deep-learning FCNN-based quantification methods were compared to the ground-truths, as shown in Fig. 3. The FCNN-based quantification approach with the LOAS schedule showed the lowest quantification errors of tissue parameters. Fig. 4 shows another digital phantom study performed with various numbers of dynamic scans (#5 to #40) to evaluate the scan efficiency of the MTC-MRF. A reduction of the dynamic scan numbers resulted in increased nRMSE values. However, the parameters estimated from the LOAS schedule with 10 dynamic scans were not significantly different from the ground-truths. Significant correlations were observed between the estimated parameters and the ground-truth for all dynamic scan numbers (p< 0.05 for all parameters) and the correlation coefficients were all over 0.8, even for #5 dynamic scans. The synthetic MRI analysis for various MRF schedules with 10 dynamic scans are shown in Fig. 5. The quantification accuracy was evaluated by calculating the mean absolute error (MAE) between the reference and tissue parameter estimates with the different MRF schedules. Corresponding MTC at 3.5 ppm, APT, and NOE signal maps were also calculated. The lowest MAE values (2.04 for k_mw, 0.53 for M₀^m, 1.33 for T₂^m, 0.05 for T₁^w, and 0.39 for MTC at 3.5 ppm, ATP, and NOE) were obtained with the LOAS schedule. In addition, good agreements were still observed for the PR and CRLB-based schedules. However, the IP and Linear schedules showed poor quantification quality.

Conclusion

We proposed a learning-based optimization framework to improve quantification accuracy and accelerate data acquisition for magnetization transfer contrast MR fingerprinting. Unlike optimization methods based on indirect measurements, the proposed LOAS method optimized scan parameters by directly minimizing quantitative errors of the tissue parameters and significantly improved the accuracy and also reduced data acquisition time. The flexible LOAS architecture could be a powerful optimization tool for MRF pulse sequence design.

Acknowledgements

No acknowledgement found.