0146
Motion correction for 3D CEST imaging without direct water saturation artefacts
Johannes Breitling1, Andreas Korzowski1, Neele Kempa1, Philip S. Boyd1, Mark E. Ladd1, Peter Bachert1, and Steffen Goerke1
1Division of Medical Physics in Radiology, German Cancer Research Center (DKFZ), Heidelberg, Germany
1Division of Medical Physics in Radiology, German Cancer Research Center (DKFZ), Heidelberg, Germany
Synopsis
In CEST-MRI, motion correction is compromised by the drastically changing image contrast at different frequency offsets and particularly at the direct water saturation. In this study, a simple extension for conventional image registration algorithms is proposed, enabling a robust and accurate motion correction of CEST-MRI data. Performance of different approaches was investigated using a ground truth dataset, generated from repeated 3D in vivo measurements at 3 T, corrupted with realistic random rigid motion patterns and noise. In comparison to the conventional image registration and a cutting-edge algorithm specifically developed for CEST-MRI, the proposed method achieved more accurate and robust results.
Introduction
Subject motion during CEST-MRI scans results in a misalignment of the acquired images, impairing the subsequent analysis and leading to large quantification errors. The correction for motion in CEST-MRI is compromised by the fact that the individual images do not only represent different motion states, but also feature different image contrasts for the different frequency offsets.1-3 Especially, the drastically different image contrast close to the water resonance results in severe misalignments of the images. The aim of this study was therefore to establish a reliable motion correction for spectral CEST data, which is at the same time robust against direct water saturation artifacts and accurate with respect to the motion estimate at the spectral position of the CEST signals of interest. To this end, we propose a simple extension for conventional image registration algorithms which uses a weighted averaging of motion parameters to identify and subsequently mitigate direct water saturation artifacts.Methods
The workflow of the proposed method is illustrated in Fig. 1. In the first step, a conventional image registration is performed (i.e. in this study the ‘slabbed head’ algorithm of MITK4, which uses a rigid transformation and Mattes’ mutual information as the image similarity metric). By assuming a primarily continuous and smooth motion, erroneously exaggerated motion estimates ($$${\bf{T}}_i$$$) can be identified and subsequently mitigated. To this end, for each frequency offset a weighted average $$${\bf\tilde{T}}_i$$$ of the surrounding motion estimates is determined. The contribution of each individual measurement to the weighted average is based on two features: (i) the reliability of its own motion estimate, and (ii) the distance (i.e. temporal) to the data point of interest. Regarding (i), the reliability is linked to the overall intensity of the image ($$${\bf M}_k$$$) and can therefore be included as a weighting factor $$$w_k = || {\bf M}_k ||^2_2$$$. Regarding (ii), the distance is considered by a weighting using a Gaussian shape as a function of the measurement number (i.e. sequence of frequency offsets) centered at the measurement of interest $$$i$$$. Combined, the weighted averages are calculated according to:$${\bf \tilde{T}}_i = \exp\left(\frac{1}{W_i}\cdot\sum_{k=0}^N w_k \cdot \exp\left(-\frac{(i-k)^2}{2(\sigma / w_k)^2}\right)\cdot \log({\bf T}_k)\right)$$
, where $$$W_i=\sum_{k=0}^N w_k \cdot \exp\left(-\frac{(i-k)^2}{2(\sigma / w_k)^2}\right)$$$ is required for normalization. A large difference, as quantified using the root-mean-square deviation ($$$d_{RMS}$$$),5 between the average and the initially estimated motion indicates the occurrence of an artefact. To mitigate the artefact, the largest significant deviation is iteratively replaced by the averaged motion estimate until there are no more significant outliers as assessed using the built-in MATLAB (MathWorks, Natick, MA) function isoutlier. Finally, the images are corrected using the last motion estimates.
Performance of the registration algorithms was investigated by adding simulated random rigid motion to a synthesized 3D in vivo dataset acquired at 3 T. Motion patterns were generated by performing a Gaussian random walk with 0 mean and a standard deviation of either 0.25 mm or 0.25° for all six degrees of freedom. To take into consideration that some subjects move strongly whereas others do not at all, the motion was scaled by a subject specific factor $$$f_{subj} \in (0,1)$$$ . Moreover, to simulate possible sudden motion an additional 1% chance was added that the motion of each offset is amplified by a factor of 10. Thereafter, the transformed data set was corrupted with Rician noise and then subjected to (i) the conventional image registration, (ii) a cutting-edge algorithm specifically developed for CEST (RPCA+PCA_R)3 with parameters optimized for this setup and (iii) the proposed method. The simulations were repeated for 100 different pseudo-random motion patterns. The quality of the results was determined using two different metrics: (i) the spectral error, i.e. root-mean-squared-error ($$$RMSE$$$) to the image without added motion, and (ii) the maximum image misalignment, with the misalignment for each image determined by the $$$d_{RMS}$$$.
Results & Discussion
As expected, the conventional image registration frequently led to severe misalignments for images close to the water resonance, which were even larger than without a motion correction (Fig. 2B, Fig. 3A). However, as these images are generally low in magnitude, this did not necessarily translate into a large spectral error (Fig. 2C, Fig. 3B). In comparison, the cutting-edge algorithm achieved a similar spectral error (Fig. 3B) while reducing also very large artefacts. Nevertheless, larger misalignments than without motion correction were still observed (Fig. 3A). In contrast, the proposed method achieved at the same time both, very accurate and robust results, reflected by significantly smaller misalignments and generally small spectral errors (Fig. 3). This is achieved by utilizing the already accurate results of the conventional image registration, but additionally identifying and mitigating erroneous severe misalignments at the direct water saturation. In future, this method could also be combined with more sophisticated algorithms (e.g. RPCA+PCA_R), potentially allowing for a more robust convergence and thus better results.Conclusion
The proposed method for motion correction in CEST-MRI allows an identification and mitigation of direct water saturation artifacts that are present after application of conventional image registration algorithms. The resulting improved robustness and accuracy enables a reliable motion correction, which is particularly crucial for an automated and carefree evaluation of spectral CEST-MRI data, e.g. for large patient cohorts or clinical routine application.Acknowledgements
No acknowledgement found.References
- Zhang Y, et al. J Magn Reson Imaging 2016;43:756-761.
- Wech T, et al. Magn Reson Med 2018;80:1979-1988.
- Bie C, et al. Quant Imaging Med Surg 2019;9(10):1697-171.
- Nolden M, et al. Int J Comput Assist Radiol Surg 2013;8:607-620.
- Jenkinson M, et al. NeuroImage 2002;17:825-841.
Figures
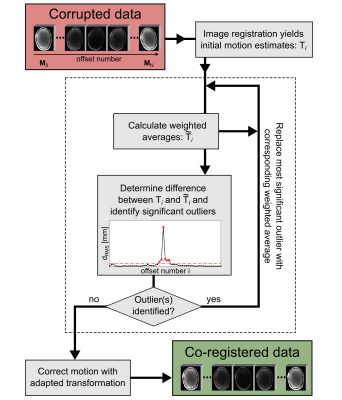
Figure 1: Illustration
of the proposed motion correction algorithm. In the first step, initial motion
estimates are obtained using a conventional image registration. For
each frequency offset a weighted average of the surrounding motion estimates is
calculated. A large difference to the initially estimated motion indicates
occurrence of an artefact, which can be mitigated by iteratively replacing the
largest significant outlier. Finally, the images are corrected using the motion estimates of the last iteration.

Figure 2: Representative
motion pattern (black) and estimates of conventional image registration (red), RPCA+PCA_R
(blue) and proposed method (green) with the five offsets close to the water
resonance (i.e. ±0.5 ppm) highlighted (A). Corresponding image misalignment (B) and spectral error (C)
with and without motion correction (colors and black respectively).
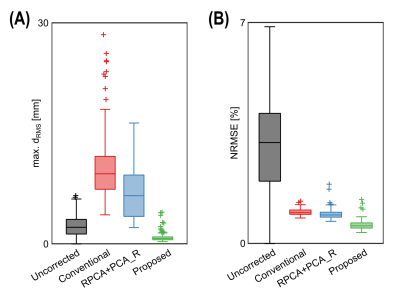
Figure 3: Statistical analysis for n=100 different motion patterns: boxplots of the overall spectral error (A) and the maximum misalignment (B) for uncorrected (black) and motion corrected
data using the conventional image registration (red), RPCA+PCA_R (blue) or
proposed method (green).