0127
Nonrigid Motion-corrected Reconstruction Using Image-space Gridding for Free-breathing Cardiac MRI1Magnetic Resonance Systems Research Lab (MRSRL), Department of Electrical Engineering, Stanford University, Stanford, CA, United States, 2Department of Bioengineering, Stanford University, Stanford, CA, United States, 3Department of Radiology, Stanford University, Stanford, CA, United States
Synopsis
Motion remains a major challenge in MRI. Many motion-corrected reconstruction methods are available, yet models are often simplified. We propose image-space gridding that resamples images onto arbitrary grids, which provides a pair of operators that represents the forward and adjoint of a nonrigid transform. This allows existing nonrigid image registration techniques to be incorporated into model-based reconstructions. We apply this method to correct for respiratory motion in free-breathing cardiac MRI. Data from individual heartbeats are binned to reconstruct image-based self-navigators. Nonrigid motion is estimated using a diffeomorphic demons algorithm, and corrected by solving an optimization problem with image-space gridding operators.
Introduction
Motion remains a major challenge in MRI. Many motion-corrected reconstruction methods are available, yet models are often simplified. A model-based iterative reconstruction$$$^{1}$$$ can compensate for complex motion by taking a nonrigid transform operator into its model. However, to our knowledge, it is nontrivial to compute the adjoint of a nonrigid transform. Using a sparse matrix$$$^{1}$$$ can be computationally expensive for high-resolution volumetric image reconstructions. Inverting a displacement field$$$^{2, 3}$$$ can result in an unmatched pair of forward and adjoint operators, which may degrade the reconstruction quality.In this work, we propose image-space gridding that resamples images onto arbitrary grids, which can represent the forward and adjoint of the nonrigid transform. This allows us to incorporate existing nonrigid image registration techniques into the reconstruction. Also, it can be accelerated using graphics processing units (GPUs) by adapting similar techniques developed for k-space gridding.
We apply this method to correct for respiratory motion in free-breathing cardiac MRI. Data from individual heartbeats are binned based on 3D translational motion estimates. Each bin enables the reconstruction of an image-based self-navigator$$$^{4, 5, 6}$$$. Nonrigid motion is estimated using a diffeomorphic demons algorithm, and corrected by solving an optimization problem with image-space gridding operators. An overview is illustrated in Figure 1.
Image-space Forward and Inverse Gridding
We consider the following optimization problem$$$^{1}$$$ (Figure 2):$$\underset{\mathrm{x}}{\mathrm{argmin}}~ \sum_{c,s} \frac{1}{2} || \mathrm{y}_{c,s} - \mathcal{G}_{c} \mathcal{S}_{s} \mathcal{T}_{c} \mathrm{x} ||_2^2 + \lambda ||\mathrm{x}||_1,~~~(1)$$
where $$$\mathrm{y}$$$ and $$$\mathrm{x}$$$ denote the measured k-space data and image, $$$\mathcal{S}$$$ and $$$s$$$ represent the sensitivity map operator and its index, $$$c$$$ denotes the heartbeat index, and $$$\mathcal{G}$$$ and $$$\mathcal{T}$$$ stand for inverse gridding and nonrigid transform operators, respectively.
We assume that the nonrigid transform operator can be represented by a displacement field $$$\overrightarrow{\mathrm{d}}$$$ as commonly used in image registration:
$$\overrightarrow{\mathrm{d}} = \mathcal{T}\overrightarrow{\mathrm{i}} - \overrightarrow{\mathrm{i}},$$
where $$$\overrightarrow{\mathrm{i}}$$$ denotes the Cartesian coordinate of a reference image, $$$I$$$. Then its registered image $$$J$$$ can be represented as:
$$J = \mathcal{T} I = I(\overrightarrow{\mathrm{i}} + \overrightarrow{\mathrm{d}}),$$
which shows that $$$J$$$ is a resampled version of $$$I$$$ on a non-Cartesian coordinate.
Gridding in k-space has been routinely used in non-Cartesian MRI$$$^{7, 8, 9}$$$. Our goal here is to apply gridding in the object domain to resample images onto arbitrary grids, which provides a pair of operators that represents the forward and adjoint of the nonrigid transform. In this case, aliasing due to resampling is manifested in k-space, and both input and output grids are in image-space. Therefore, image-space gridding can be derived by adding a Fourier transform operator $$$\mathcal{F}$$$ to k-space gridding as follows (Figure 3):
$$\mathcal{T}: \mathcal{F} \rightarrow \mathcal{Z} \rightarrow \frac{1}{h} \rightarrow \mathcal{F}^{-1} \rightarrow \text{convolution and sampling},$$ $$\mathcal{T}^H: \text{convolution and sampling} \rightarrow \mathcal{F} \rightarrow \frac{1}{h^*} \rightarrow \mathcal{Z}^{T} \rightarrow \mathcal{F}^{-1},$$
where $$$\mathcal{Z}$$$ and $$$\mathcal{Z}^{T}$$$ represent zero-padding and unzero-padding operators respectively, and $$$\frac{1}{h}$$$ denotes the preemphasis step that negates the convolution operation$$$^{8}$$$.
Nonrigid Motion-corrected Reconstruction in Free-breathing Cardiac MRI
For each heartbeat, we collect segmented cones interleaves that sparsely cover the entire k-space$$$^{10, 11}$$$ along with a 3D image-based navigator (iNAV)$$$^{12}$$$.Beat-to-beat 3D translational motion is estimated using the iNAVs, and compensated by applying linear phases to the k-space measurements. Subsequently, segmented cones data from individual heartbeats are binned using k-means clustering based on the 3D translational motion estimates.
An image-based self-navigator is reconstructed from each bin$$$^{4, 5, 6}$$$, and the self-navigator from the bin with the least variance of 3D translational motion is chosen as the reference. Nonrigid motion manifested between the reference and other self-navigators is estimated using a diffeomorphic demons algorithm.
Nonrigid motion-corrected reconstruction is achieved by solving (1) iteratively with image-space gridding operators.
Methods
For nonrigid motion estimation, we used a symmetric forces diffeomorphic demons algorithm implemented in SimpleITK$$$^{13, 14, 15}$$$. ESPIRiT$$$^{16}$$$ was used for estimating sensitivity maps. L1-FISTA$$$^{17}$$$ was used with 400 iterations for solving (1).Two subjects were studied on a 1.5T GE Signa scanner using a GE 8-channel cardiac coil. An ATR-SSFP acquisition$$$^{18}$$$ with a segmented phyllotaxis 3D cones trajectory$$$^{10}$$$ (RES=1.2-mm) was carried out over 610 heartbeats. For each heartbeat, a 3D iNAV was also collected using a 32-interleave cones trajectory (RES=4.4-mm)$$$^{12}$$$. The primary data was partitioned into four bins using motion estimates from the 3D iNAVs.
Results
The bottom row of Figure 3 illustrates the reconstruction results of the following toy problem:$$\underset{\mathrm{I}}{\mathrm{argmin}}~ \frac{1}{2} || I - \mathcal{T} J ||_2^2 + \lambda ||I||_1,$$which suggests that the derived image-space gridding operators are suitable for model-based iterative reconstructions.
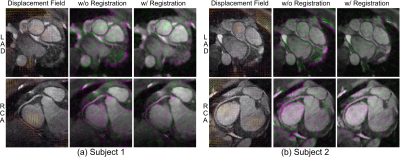
Figure 4 illustrates reconstructed slices near the left anterior descending artery (LAD) and right coronary artery (RCA). The proposed method exhibited improved sharpness not only near the coronary arteries but also in non-cardiac regions compared to 3D translational motion-corrected reconstruction.
The leftmost columns of Figure 5 show estimated displacement fields. To assess the validity of the measured nonrigid motion, we overlayed reference and non-reference slices with purple and green colors, which are illustrated in the middle and rightmost columns, respectively. We can observe that discrepancies among image-based self-navigators were significantly reduced.
Conclusion
A new nonrigid motion-corrected reconstruction using image space gridding was presented, which allows existing nonrigid image registration techniques to be incorporated into the model-based reconstruction. Also, a novel approach for nonrigid motion-correction for free-breathing cardiac MRI was demonstrated.Acknowledgements
The authors gratefully acknowledge the support from NIH grant R01 HL127039, R01 EB026136, and GE Healthcare.References
1. F. Odille, P. A. Vuissoz, P. Y. Marie, and J. Felblinger, "Generalized reconstruction by inversion of coupled systems (GRICS) applied to free-breathing MRI," Magnetic Resonance in Medicine, vol. 60, no. 1, pp. 146–157, 2008.
2. M. Chen, W. Lu, Q. Chen, K. J. Ruchala, and G. H. Olivera, "A simple fixed-point approach to invert a deformation field," Medical Physics, vol. 35, no. 1, pp. 81–88, 2008.
3. N. R. Huttinga, T. Bruijnen, C. A. van den Berg, and A. Sbrizzi, "Nonrigid 3D motion estimation at high temporal resolution from prospectively undersampled k-space data using low-rank MR-MOTUS," Magnetic Resonance in Medicine, 2020.
4. H. Bhat, L. Ge, S. Nielles-Vallespin, S. Zuehlsdorff, and D. Li, "3D radial sampling and 3D affine transform-based respiratory motion correction technique for free-breathing whole-heart coronary MRA with 100% imaging efficiency," Magnetic Resonance in Medicine, vol. 65, no. 5, pp. 1269–1277, 2011.
5. J. Pang, H. Bhat, B. Sharif, Z. Fan, L. E. Thomson, T. LaBounty, J. D. Friedman, J. Min, D. S. Berman, and D. Li, "Whole-heart coronary MRA with 100% respiratory gating efficiency: self- navigated three-dimensional retrospective image-based motion correction (TRIM)," Magnetic Resonance in Medicine, vol. 71, no. 1, pp. 67–74, 2014.
6. M. Henningsson, C. Prieto, A. Chiribiri, G. Vaillant, R. Razavi, and R. M. Botnar, "Whole-heart coronary MRA with 3D affine motion correction using 3D image-based navigation," Magnetic Resonance in Medicine, vol. 71, no. 1, pp. 173–181, 2014.
7. V. Rasche, R. Proksa, R. Sinkus, P. Bornert, and H. Eggers, "Resampling of data between arbitrary grids using convolution interpolation," IEEE Transactions on Medical Imaging, vol. 18, no. 5, pp. 385–392, 1999.
8. P. J. Beatty, D. G. Nishimura, and J. M. Pauly, "Rapid gridding reconstruction with a minimal oversampling ratio," IEEE Transactions on Medical Imaging, vol. 24, no. 6, pp. 799–808, 2005.
9. J. A. Fessler, "On NUFFT-based gridding for non-Cartesian MRI," Journal of Magnetic Resonance, vol. 188, no. 2, pp. 191–195, 2007.
10. M. O. Malavé, C. A. Baron, N. O. Addy, J. Y. Cheng, P. C. Yang, B. S. Hu, and D. G. Nishimura, "Whole-heart coronary MR angiography using a 3D cones phyllotaxis trajectory," Magnetic Resonance in Medicine, vol. 81, no. 2, pp. 1092–1103, 2019.
11. K. E. Jang, D. G. Nishimura, and S. S. Vasanawala, "Segmented Twin-resolution Acquisition of Cones Trajectory (STACY) and Coalesced Image Navigator for Free-breathing Cardiac MRI," in Proceedings of the 28th Annual Meeting of the ISMRM, 2019.
12. N. O. Addy, R. R. Ingle, J. Luo, C. A. Baron, P. C. Yang, B. S. Hu, and D. G. Nishimura, “3D image-based navigators for coronary MR angiography,” Magnetic Resonance in Medicine, vol. 77, no. 5, pp. 1874–1883, 2017.
13. T. Vercauteren, X. Pennec, A. Perchant, N. Ayache, et al., "Diffeomorphic demons using ITKs finite difference solver hierarchy," The Insight Journal, vol. 1, 2007.
14. M. M. McCormick, X. Liu, L. Ibanez, J. Jomier, and C. Marion, "ITK: enabling reproducible research and open science," Frontiers in Neuroinformatics, vol. 8, p. 13, 2014.
15. B. C. Lowekamp, D. T. Chen, L. Ibáñez, and D. Blezek, "The design of SimpleITK," Frontiers in neuroinformatics, vol. 7, p. 45, 2013.
16. M. Uecker, P. Lai, M. J. Murphy, P. Virtue, M. Elad, J. M. Pauly, S. S. Vasanawala, and M. Lustig, "ESPIRiT – an eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA," Magnetic Resonance in Medicine, vol. 71, no. 3, pp. 990–1001, 2014.
17. A. Beck and M. Teboulle, "A fast iterative shrinkage-thresholding algorithm for linear inverse problems," SIAM Journal on Imaging Sciences, vol. 2, no. 1, pp. 183–202, 2009.
18. H. H. Wu, P. T. Gurney, B. S. Hu, D. G. Nishimura, and M. V. McConnell, "Free-breathing multiphase whole-heart coronary MR angiography using image-based navigators and three- dimensional cones imaging," Magnetic Resonance in Medicine, vol. 69, no. 4, pp. 1083–1093, 2013.
Figures
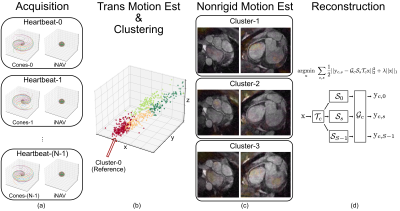
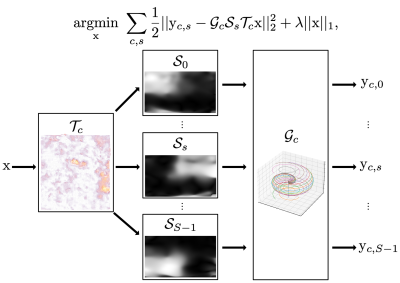


Figure 4. Reconstructed slices near LAD and RCA. The proposed method exhibited improved sharpness not only near the coronary arteries (orange arrows) but also in non-cardiac regions (green arrows) compared to 3D translational motion-corrected reconstruction.