0126
LAPNet: Deep-learning based non-rigid motion estimation in k-space from highly undersampled respiratory and cardiac resolved acquisitions
Thomas Küstner1,2, Jiazhen Pan3, Haikun Qi2, Gastao Cruz2, Kerstin Hammernik3,4, Christopher Gilliam5, Thierry Blu6, Sergios Gatidis1, Daniel Rueckert3,4, René Botnar2, and Claudia Prieto2
1Department of Radiology, Medical Image and Data Analysis (MIDAS), University Hospital of Tübingen, Tübingen, Germany, 2School of Biomedical Engineering and Imaging Sciences, King's College London, London, United Kingdom, 3AI in Medicine and Healthcare, Klinikum rechts der Isar, Technical University of Munich, München, Germany, 4Department of Computing, Imperial College London, London, United Kingdom, 5RMIT, University of Melbourne, Melbourne, Australia, 6Chinese University of Hong Kong, Hong Kong, Hong Kong
1Department of Radiology, Medical Image and Data Analysis (MIDAS), University Hospital of Tübingen, Tübingen, Germany, 2School of Biomedical Engineering and Imaging Sciences, King's College London, London, United Kingdom, 3AI in Medicine and Healthcare, Klinikum rechts der Isar, Technical University of Munich, München, Germany, 4Department of Computing, Imperial College London, London, United Kingdom, 5RMIT, University of Melbourne, Melbourne, Australia, 6Chinese University of Hong Kong, Hong Kong, Hong Kong
Synopsis
Estimation of non-rigid motion is an important task in respiratory and cardiac motion correction. Usually, this problem is formulated in image space via diffusion, parametric-spline or optical flow methods. However, image-based registration can be impaired by aliasing artefacts or by estimating in low image resolution in cases of highly accelerated acquisitions. In this work, we propose a novel deep learning-based non-rigid motion estimation directly in k-space, named LAPNet. The proposed method, inspired by optical flow, is compared against registration in image space and tested for respiratory and cardiac motion as well as different acquisition trajectories providing a generalizable diffeomorphic registration.
Introduction
Fast and accurate estimation of non-rigid motion is an important task in respiratory and cardiac motion corrected image reconstruction. Several motion correction methods1-4 have been proposed, which usually rely on motion estimation from motion-resolved undersampled datasets. These methods exploit sparsity5 or low-rank redundancies6 in the spatial and/or temporal directions7-11 to reconstruct motion-resolved images. Motion between the different motion states is commonly estimated in image space via diffusion12, parametric-spline13 or optical flow14 registration methods. However, in case of highly undersampled data, aliasing artefacts in the image (during or after reconstruction) can impair the image-based registration. Therefore, carrying out an aliasing-free and fast registration in k-space for accelerated acquisitions would be desirable.The feasibility of a non-rigid registration in k-space has been recently demonstrated11, however the practical implementation runs several hours to derive a 3D deformation field, due to the increased computational complexity. In this work, we propose the translation of the non-rigid registration in k-space concept into a deep-learning registration, denoted as LAPNet. The proposed method renders computationally efficient yet generalizable to different tasks. We investigate the application of LAPNet for non-rigid motion estimation of 3D respiratory-resolved thoracic and 2D cardiac CINE imaging in a cohort of 50 and 38 subjects, respectively. Cartesian and radial trajectories are considered, for 3D respiratory-resolved thoracic and 2D cardiac CINE respectively, to investigate the architectures capability to generalize to different imaging scenarios.
Methods
The non-rigid registration in k-space is formulated following the concepts of Local-All Pass (LAP)15-17, an optical-flow based registration. The key idea of LAP is that, under the assumption of smoothly varying flows, any non-rigid deformation can be regarded as a sum of local rigid displacements. These displacements can be modeled as local all-pass filter operations. Under the assumption of local brightness consistency, the optical flow equation of a rigid displacement in a local bounded neighborhood $$$\underline{x} \in \mathcal{W}$$$ can be stated as$$\rho_r(\underline{x}) = \rho_m(\underline{x}-\underline{u}_r) \Leftrightarrow \nu_r(\underline{k}) = \nu_m(\underline{k}) \mathrm e^{-j \underline{u}_r^T \underline{k}}$$
for deforming a moving image $$$\rho_m$$$ to a reference image $$$\rho_r$$$ via a deformation field $$$\underline{u}_r$$$ at position $$$\underline{x} = \lbrack x,y,z \rbrack^T$$$, with $$$\nu_m(\underline{k})$$$ and $$$\nu_r(\underline{k})$$$ being the moving and reference k-spaces at $$$\underline{k} = \lbrack k_x,k_y,k_z\rbrack^T$$$. The linear phase ramp can be regarded as an all-pass filter $$$\hat{h}(\underline{k},\underline{x})=\mathrm{e}^{-j \underline{u}_r^T(\underline{x})\underline{k}}=\hat{f}(\underline{k})/\hat{f}(-\underline{k})$$$ that can be split into a forward $$$\hat{f}(\underline{k})$$$ and backward filter $$$\hat{f}(-\underline{k})$$$ which is all-pass by design18, i.e. $$$|\hat{h}(\underline{k})|=1$$$. Non-rigid registration can thus be modelled as estimating the appropriate local all-pass filters. Consequently, the k-space non rigid registration can be formulated as
$$\min\limits_{\lbrace c_n\rbrace}\sum\limits_{\underline{k}\in \mathbb{R}^3}\mathcal{D}\left(T(\underline{k})\ast\left(\hat{f}(\underline{k})\nu_m(\underline{k})\right),T(\underline{k})\ast\left(\hat{f}(-\underline{k})\nu_r(\underline{k})\right)\right)$$
$$\text{s.t. } \hat{f}(\underline{k})=\hat{f}_0(\underline{k})+\sum\limits_{n=1}^N c_n\hat{f}_n(\underline{k})\quad \forall\underline{k}\in \mathbb{R}^3$$
for which under phase-modulated tapering functions $$$T(\underline{k})$$$ in k-space $$$\nu$$$ the $$$N$$$ optimal filter coefficients $$$c_n$$$ for bases functions $$$\hat{f}$$$ are estimated by minimizing the dissimilarity $$$\mathcal{D}$$$ (e.g. root-mean-squared error) between $$$\nu_m$$$ and $$$\nu_r$$$. Tapering (convolution by Fourier-transformed window and regridding with bilinear interpolation) in k-space is equivalent to windowing in image space. The diffeomorphic flow $$$\underline{u}$$$ in image domain can be directly derived from the all-pass filter
$$\underline{u}=\left.j\frac{\partial\ln \hat{h}(\underline{k})}{\partial\underline{k}}\right|_{\underline{k}=\underline{0}}\Leftrightarrow\underline{u}=2\left\lbrack\frac{\sum_\underline{x}xf(\underline{x})}{\sum_\underline{x}f(\underline{x})},\frac{\sum_\underline{x}yf(\underline{x})}{\sum_\underline{x}f(\underline{x})},\frac{\sum_\underline{x}zf(\underline{x})}{\sum_\underline{x}f(\underline{x})}\right\rbrack^T$$
A convolutional neural network is proposed in Fig. 1 that solves the minimization, i.e. learns the LAP filters $$$\hat{f}$$$ from the tapered and complex-valued k-space patches $$$\nu_m$$$ and $$$\nu_r$$$ and outputs the in-plane deformation at the central position of the current windowing $$$\mathcal{W}$$$/tapering $$$T$$$. To obtain a 3D non-rigid deformation field $$$\underline{u}$$$, the registration is performed on orthogonal spatial directions in a sliding window fashion.
The network is trained in a supervised manner on pairs of moving $$$\nu_m$$$ and reference k-spaces $$$\nu_r$$$ with the corresponding ground-truth motion field $$$\underline{u}_\text{GT}$$$ derived from an image-based LAP by minimizing the squared end-point error loss $$$\sum_{i\in\lbrace x,y,z\rbrace}(u_{\text{GT},i}-u_i)^2$$$ with an ADAM optimizer (learning rate scheduler with initial $$$2.5\cdot 10^{-4}$$$, batch size 64, 60 epochs). Respiratory and cardiac motion-resolved data was obtained as stated in Table 1. Training is performed on 46 (respiratory) and 34 (cardiac) subjects with varying undersampling strategies (3D Cartesian variable-density Poisson Disc and 2D golden radial) and for changing acceleration factors 2x-30x (respiratory), 2x-16x (cardiac). Qualitative and quantitative (end-point-error, end-angulation-error, SSIM, NRMSE) testing is conducted on 4 subjects in each cohort in comparison to an image-based deep learning (FlowNet-S19) and a conventional cubic B-Spline image registration (NiftyReg20).
Results and Discussion
Fig. 2 and 3 depict examples of the respiratory and cardiac image database for different undersampling factors in comparison to FlowNet-S and NiftyReg. The proposed LAPNet provides a 3D non-rigid registration from undersampled k-space data for different imaging (GRE, bSSFP) and undersampling (3D Cartesian, 2D radial) scenarios. For highly accelerated acquisitions, image-based registrations fail whereas LAPNet still provides similar and consistent registration. Superior performance of LAPNet is also reflected in the quantitative analysis over changing acceleration factors in Fig. 4. LAPNet registrations can be performed in ~18s in contrast to ~16s for FlowNet-S and ~83s for NiftyReg.Conclusion
We proposed a deep-learning based non-rigid registration, termed LAPNet, which performs registration directly on the acquired k-space data. Results indicate improved performance of LAPNet in comparison to image-based registration approaches for high acceleration factors and changing imaging conditions.Acknowledgements
The authors would like to thank Carsten Gröper, Gerd Zeger, Reza Hajhosseiny and Pier Giorgio Masci for data acquisition and Brigitte Gückel for study coordination.References
1. Block. Magnetic Resonance in Medicine 2007;57(6).2. Cheng. Journal of Magnetic Resonance Imaging 2015;42(2).
3. Cruz. Magnetic Resonance in Medicine 2017;77(5).
4. Küstner. Magnetic Resonance in Medicine 2017;78(2).
5. Lustig. Magnetic Resonance in Medicine 2007;58(6).
6. Otazo. Magnetic resonance in medicine 2015;73(3).
7. Liu. Magnetic Resonance Imaging 2019;[Epub ahead of print].
8. Mohsin. Magnetic Resonance in Medicine 2017;77(3).
9. Caballero. IEEE Trans Med Imag 2014;33(4).
10. Jung. Phys Med Biol 2007;52(11).
11. Küstner. Proc International Society for Magnetic Resonance in Medicine (ISMRM) 2020.
12. Thirion. Medical image analysis 1998;2(3).
13. Rueckert. IEEE Transactions on Medical Imaging 1999;18(8).
14. Horn. Artificial intelligence 1981;17(1-3).
15. Gilliam. IEEE International Symposium on Biomedical Imaging (ISBI) 2016. p282-5.
16. Küstner. Proc ISMRM Workshop on Motion Correction in MRI and MRS 2017.
17. Küstner. Medical image analysis 2017;42.
18. Gilliam. IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP) 2015. p1533-7.
19. Dosovitskiy. IEEE International Conference on Computer Vision (ICCV) 2015. p2758-66.
20. Modat. Comput Meth Prog Bio 2010;98(3).
21. Küstner. Magnetic Resonance in Medicine 2020.
Figures
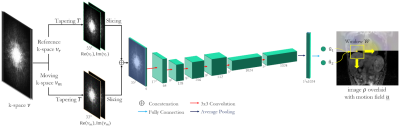
Fig. 1: Proposed LAPNet to perform non-rigid registration in k-space.
Moving νm and reference νr k-spaces are tapered to a smaller support W. The bundle of
k-space patches is processed in a succession of convolutional filters (kernel
sizes and channels are stated) to estimate the in-plane flows u1,u2 at the central voxel location determined by
the tapering T/window W for size 33x33x33. Overall 3D
deformation field u is obtained from a sliding window over all
voxels in orthogonal directions.

Fig. 2: Respiratory non-rigid
motion estimation in a patient with a liver metastasis in segment VIII. Motion
displacement is estimated by the proposed LAPNet in k-space in comparison to
image-based non-rigid registration by FlowNet-S (neural network) and NiftyReg
(cubic B-Spline). Estimated flow displacement are depicted in coronal and
sagittal orientation. Undersampling was performed prospectively with a 3D
Cartesian random undersampling for 8x and 30x acceleration.
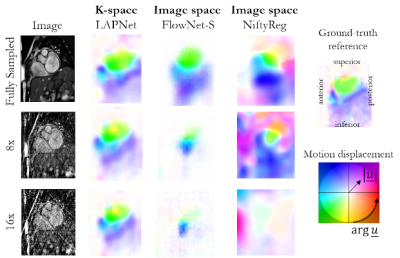
Fig. 3: Cardiac non-rigid motion estimation in a patient with
myocarditis. Motion displacement is estimated by the proposed LAPNet in k-space
in comparison to image-based non-rigid registration by FlowNet-S (neural
network) and NiftyReg (cubic B-Spline). Estimated flow displacement are
depicted in short axis orientation. Undersampling was performed retrospectively
with a 2D radial undersampling for 8x and 16x acceleration.
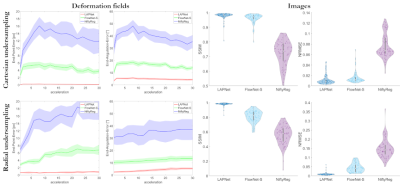
Fig. 4: End-point error and end-angulation error between
predicted and ground-truth deformation fields as well as structural similarity
index (SSIM) and normalized root mean squared error (NRMSE) between registered
moving and reference image of the proposed LAPNet in k-space, image-based
FlowNet-S (neural network) and NiftyReg (cubic B-Spline). Mean (solid line) and
standard deviation (shaded area) are shown for changing acceleration factors of
3D Cartesian and 2D golden radial undersampling.
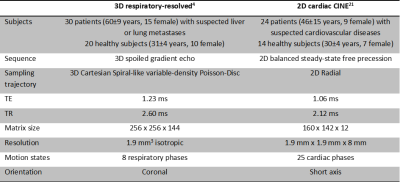
Table 1: Motion-resolved MR imaging datasets and acquisition parameters.