Introduction

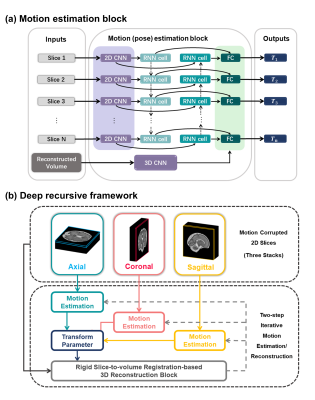
Fetal MR neuroimaging is usually undermined by severe, uncontrollable, and arbitrary fetal motion, imposing enormous challenges for fetal brain 3D volumetric reconstruction and disease detection^1-2. Conventional motion correction and reconstruction of multi-slice T1/T2-weighted fetal brain MRI involves slice-to-volume registration (SVR) and super-resolution reconstruction (SRR) of multi-oriented 2D multi-slice images to solve an inverse problem^3-5. However, the method is susceptible to rapid large-scale motion and is excessively time-consuming, which is impractical in clinical settings. In this work, a deep recursive framework (DeepRF) was proposed by mimicking iterations between rigid SVR and 3D reconstruction using deep learning. We compared the method to several state-of-the-art learning-based fetal motion estimation algorithms using simulated motion-corrupted data.

Methods

Data acquisition: In-utero MRI scans of 95 fetal brain MRI (gestational age (GA): 23.3-40.0 weeks) with at least three orthogonal orientations were collected under IRB approval. The data were acquired on a 3T Siemens Skyra scanner (Siemens Healthineers, Erlangen, Germany) with an abdominal coil, using T2-weighted half-Fourier single-shot turbo spin-echo (HASTE) sequence with the following protocol: TR/TE = 800/97 ms, in-plane resolution = 1.09 × 1.09 mm, FOV = 256 × 200 mm, 35-55 slices with slice thickness = 2 mm, GRAPPA factor = 2.

Data preprocessing: Bias field was corrected using the N4 algorithm⁶. Then, in-plane motion correction and SRR with an isotropic spacing (0.8mm) were automatically performed via NiftyMIC toolkit⁷. Fetal brain was extracted by manual masking, followed by 3D non-local means denoising⁸ and intensity normalization. Next, reconstructed fetal brain volumes were rigidly registered to the corresponding templates⁹, center-aligned and resized into 144*144*120 by padding zeros in the surrounding regions. Note that the super-resolution reconstructed volume from 2mm slices was used as ground truth.

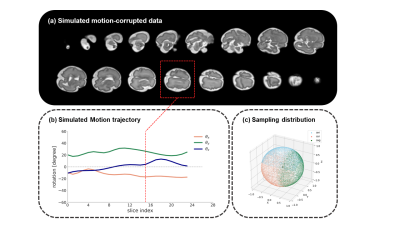
Motion simulation: Fetal brain movement was simulated by 3D rigid transformation. Here, we primarily considered rotational motion, and the rotation angle was sampled from a continuous motion curve generated from a random Markov process and spline interpolation, with the mean between [-45, 45] degrees (Figure 1b). The average velocity of motion was simultaneously regulated by control points. The motion was separated applied to axial, coronal and sagittal orientations, and therefore, the simulated motion covered all possible poses (Figure 1c). In this work, we temporarily simulated non-interleaved acquisition that covered the entire fetal brain with 4 mm slice-thickness.

Network architecture: The network is illustrated in Figure.2. For motion estimation, the slices $$$I_s$$$ were fed into a 2D CNN for feature extraction and then went through a bidirectional recurrent network followed by fully-connected layers. The predicted parameters were subsequently utilized for motion correction and 3D reconstruction. We employed a scattered data approximation¹⁰ with decreasing Gaussian spatial blurring as the reconstruction transformer that facilitated the network computation. A roughly reconstructed volume $$$V$$$ from motion-corrected axial/coronal/sagittal data was taken back into a 3D CNN and then concatenated to the fully-connected layers. The network weights were shared across iterations and optimized using an end-to-end scheme. The loss $$$L$$$ includes the MSE of rigid transform parameters and the similarity between the estimated images and ground truth. $$L = {L_{sim}}({\hat \phi _s},{\phi _s}) + \lambda {L_{sim}}\left( {{\rm{\Omega }}\left( {{I_s},{{\hat \phi }_s}} \right),V} \right)$$ where $$$L_{sim}$$$ denotes the similarity metric, i.e., MSE, $$${\phi _s}$$$ and $$${\hat \phi _s}$$$ are the rotational angle and its estimation, $$${\rm{\Omega }}$$$ denotes 3D reconstruction, and the two loss terms are adjusted by a weighting $$$\lambda$$$.

Altogether, 82 (GA: 23.3-40.0w), 5 (GA: 26.1-32.0w), and 8 (GA: 24.6-35.4w) fetuses were used for training, validation and testing. The performance of DeepRF was compared to other state-of-the-art learning-based fetal brain motion estimation methods, including Deep Pose Estimation¹¹, anchor-point-based SVRnet¹², Deep Predictive Motion Tracking¹³.

Results

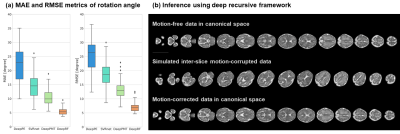
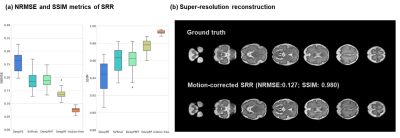
As shown in Figure 3a, the DeepRF achieved the least mean absolute error (MAE) of 5.49º and root MSE of 7.23º, compared to other learning-based methods on the simulated motion-corrupted slices. The average time for motion correction is 15.9 seconds, with nearly 50-fold speed acceleration compared to the conventional two-step iterative SVR-SRR method.

We performed SRR on the motion-corrected data from different networks, and DeepRF achieved the best reconstruction accuracy with the least normalized root mean square error (NRMSE) of 0.136 and the highest structural similarity index (SSIM) of 0.977 with the ground truth (2mm slice-thickness acquisition) (Figure 4), which was close to the SRR of motion-free data with NRMSE of 0.076 and SSIM of 0.993 (4mm slice-thickness acquisition).

Discussion and conclusion

The proposed DeepRF outperformed the other state-of-the-art learning-based methods for fetal brain motion estimation and correction, and also increased the 3D reconstruction efficiency with close precision compared to the traditional SRR scheme. The superior performance of the DeepRF may be associated with the network architecture that replicates the iterative SVR and reconstruction process and incorporation of the image similarity and transform matrices, as well as the use of bidirectional recurrent network that takes into account the series of motion between successive slices. The high accuracy and computational efficiency of DeepRF makes it promising for fetal brain MRI analysis, although generalizability of the current network needs to be further tested in more complicated situations.

Acknowledgements

This work is supported by the Ministry of Science and Technology of the People’s Republic of China (2018YFE0114600), National Natural Science Foundation of China (61801424 and 81971606).