Introduction

Acoustic noise and patient motion are two main obstacles in diagnostic MRI, causing additional stress for the patient, complications for the medical staff and extra cost for the healthcare system^1,2. Each issue has previously been investigated separately: methods to combat motion include navigator echoes³, self-navigation⁴ and external tracking devices⁵, while acoustic noise can be reduced using smooth gradient waveforms⁶ or Zero Echo Time (ZTE) pulse sequences^7,8.

In this work we address both issues, by combining silent ZTE with a self-navigated phyllotaxis trajectory for retrospective motion correction. We call this method MERLIN for Motion Elimination in Radial acquisition Leveraging Interleaved Navigators.

Methods

ZTE sequences acquire data along radial-out spokes during the free induction decay. With a TR on the order of ≈1-3ms, flip angles 1-5°, and RF spoiling between excitations, ZTE sequences can be treated as spoiled gradient echo sequences⁹, making them suitable for magnetisation preparation, like MPRAGE¹⁰.

MERLIN adds two components to a standard ZTE pulse sequence: an interleaved k-space trajectory for self-navigation, and a retrospective motion correction framework. Here we describe an example using IR-ZTE for high-resolution T₁w neuroimaging.

A single healthy volunteer was scanned on a 3T GE MR750 (GE Healthcare, Chicago, IL), after providing written consent. IR-ZTE data were acquired with readout BW=±31.25 kHz, FOV=192x192x192mm³, resolution=1x1x1mm³, TI=450ms, FA=3°, TR=1.8ms, 384 spokes per readout segment, 108,288 spokes in total, and acquisition time=5:42min. IR-ZTE images were reconstructed with and without motion correction, using an iterative TGV-regularized gridding reconstruction (λ=0.00001)¹¹. All ZTE image reconstruction was performed using the RIESLING toolbox (https://github.com/spinicist/riesling).

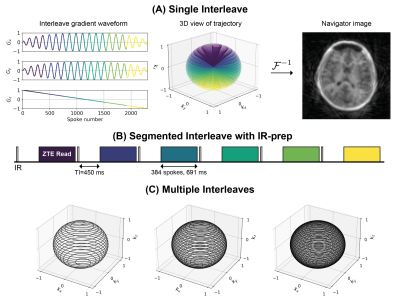
A Self-navigated 3D Radial Trajectory
To maintain a silent acquisition, the change in gradient amplitude between excitations has to be small. The spiral phyllotaxis trajectory^12,13 can be formulated to provide self-navigated high-resolution imaging while still requiring only minimal gradient switching for silent operation. Our trajectory was designed to have 47 interleaves (N_int), each with 2304 spokes (N_spi). An interleave is defined as a single spiral path covering k-space from top to bottom (Figure 1A). The azimuthal φ_i,k and polar θ_i,k angles for spoke i in interleave k are given by
$$
\phi_{i,k}=i\phi_G\cdot{F(s)}+k\phi_G, \quad \theta_{i,k}=\cos^{-1}\left(1-\frac{2\cdot{N}_{int}\cdot{i}}{N-1}-\frac{2\cdot{k}}{N-1}\right)
$$
$$
i=0...N_{spi}-1,\quad{k}=0...N_{int}-1,\quad{N}=N_{spi}\cdot{N_{int}}
$$
where φ_G is the golden angle, F(·) is the Fibonacci sequence, and s is the smoothness factor, here s=10 which results in an azimuthal step of 2.9° (mod(F(10)·φ_G,2π)). The interleaves were divided into 6 segments (N_seg) to allow for IR preparation (Figure 1B). Subsequent interleaves are rotated by the golden angle relative to each other to produce pseudo-random, uniform, k-space coverage (Figure 1C).

Motion Correction
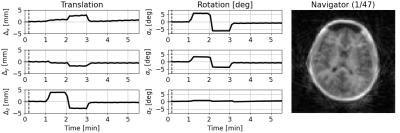
Interleaves were reconstructed using CG-SENSE¹⁴ at a lower-resolution (3x3x3mm³, effective R=5.6) to produce motion navigators. These were co-registered using a 3D rigid body transformation (VersorRigid3DTransform) implemented in ITK¹⁵. Estimated translations (Δ_x, Δ_y, Δ_z) were corrected in k-space by applying a phase ramp, and rotations (α_x, α_y, α_z) were corrected by rotating the trajectory¹⁶, producing a corrected k-space dataset for reconstruction with TGV as described above.

Motion Experiment
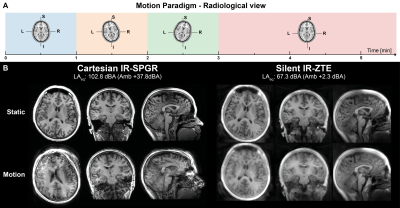
Two acquisitions were performed, one without and one with motion; for the latter, the subject was asked to repeat a pattern of rotating the head in the coil according to instructions (Figure 2A). For comparison, a conventional, 3D Cartesian IR-SPGR scan was acquired, also with TI=450ms, acquisition time=5:36, also with and without motion. Acoustic noise measurements were performed for a period of 30s in the centre of the bore.

Results

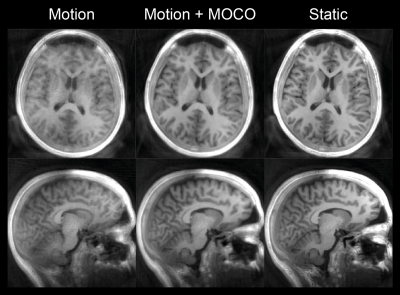
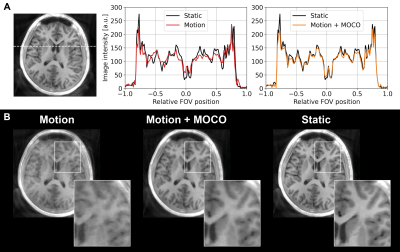
Figure 2B shows IR-SPGR compared to IR-ZTE reconstructed without motion correction. The repeated sampling of centre of k-space in IR-ZTE results in improved robustness to motion, but motion nevertheless resulted in significant blurring. The acoustic noise from IR-ZTE was only 2.3dBA over the ambient compared to 37.8dBA above with IR-SPGR.

The estimated motion parameters shown in the animated Figure 3 clearly follows the movement pattern that the volunteer was instructed to perform, with step-like changes at 1, 2, and 3 minutes into the scan. Figure 4 shows the IR-ZTE data with motion correction, showing markedly improved image quality. Figure 5A shows a line-profile in the axial-plane which clearly shows how the image intensity in the corrected image closely follows the static image. The magnified area in Figure 5B shows how the white and gray matter boundaries are better resolved with motion correction.

Discussion and Conclusion

In this work we have presented MERLIN, a framework for self-navigated motion correction using silent ZTE. MERLIN only requires a simple modification to the k-space trajectory typically used in ZTE imaging and is also consistent with other types of contrast preparation (e.g., T₁, T₂, DWI, MRA, etc.).

To maintain a near-silent acquisition, the gradient steps between spokes have to be kept small, which limits the trajectory to spiral-like patterns. With the IR-ZTE protocol used here, 40% of the acquisition time is spent on the inversion time. This prolongs the time required for each navigator, here about to ~7s. The duration of each navigator can be reduced by using fewer spokes, but at the expense of faster gradient switching and higher acoustic noise, as well as reduced SNR in each navigator. Further work will focus on reducing the time required for each navigator to improve the temporal resolution of the motion estimates.

Acknowledgements

This work was supported by the Wellcome/EPSRC Centre for Medical Engineering [WT203148/Z/16/Z], the National Institute for Health Research (NIHR) Wellcome Trust King’s Clinical Research Facility at King's College Hospital, and GE Healthcare.