Introduction

Diffusion MRI (dMRI) is a widely used imaging modality to study neurological changes non-invasively. The nanoscale water displacement arising from the Brownian motion within the tissue spaces, is encoded using large bipolar gradients in dMRI. The resulting MRI signal is sensitive to cellular changes at the microstructural level, such as those accompanying neurological disorders. However, the current mesoscale diffusion MR imaging using standard single-shot EPI technique, is of low spatial resolution with respect to the micro-level tissue features that are being probed^1-2. The large voxel sizes lead to several confounds in dMRI-based microstructural studies.
The confounds arising from low spatial resolution can be reduced either using multi-shot EPI (msEPI) methods or using extensive measurements in the q-space with the help of biophysical modeling^1-2 or by combining these two approaches. However, the practical utility of both of the above approaches are limited due to their long scan-time. Here, we present a novel acceleration and reconstruction method that enables msEPI techniques to be used for multi-shell dMRI studies.

Methods

To achieve high acceleration, we propose to under-sample the joint k-q space of dMRI in two ways. First, we use highly accelerated msEPI for k-q space under-sampling. Here, if the fully-sampled case consists of N_fs shots, the accelerated case will only use N_us (<N_fs) shots, giving an acceleration factor of N_fs/N_us. Moreover, the specific N_us shots at a given q-space point is randomly chosen out of the N_fs shots, resulting in an incoherent sampling pattern in the k-q-space. Because the aliasing patterns arising from such under-sampling are incoherent, we can also perform a second under-sampling in the k-q-domain, by completely skipping the sampling of some q-space points. Thus, if the full q-space consist of N_fq points, we only sample N_uq points, giving a total acceleration of N_fq*N_fs/N_us/N_uq in the joint k-q domain (see figure 1).

At very high acceleration factors, the reconstruction of the data from the proposed incoherent k-q under-sampling presents a challenge, especially the recovery of the missing volumes. We develop a joint reconstruction scheme where our goal to recover the entire set of diffusion weighted images (DWIs) simultaneously, by exploiting appropriately designed k-space/image-space and q-space constraints. In particular, the q-space constraint is the critical component for the successful joint recovery, by providing a voxel-wise constraint along the q-domain capable of recovering the missing q-space points.

We propose to make use of a deep learned q-space manifold prior for the joint recovery. Specifically, we pre-learn the q-space manifold that represents the diffusion signals over multiple shells, and are suitable to represent in-vivo diffusion signals. Rather than learning the q-space manifold from in-vivo training data which are hard to come by, we define the q-space manifold based on detailed biophysical modeling. We generate training samples corresponding to the desired q-space manifold using the biophysical model and train a denoising autoencoder neural network using the training data³. The pre-learned q-space manifold prior is then used in the joint recovery of the multi-shell data as :
$$ \mathbf{S}^{^*}\!\!~=~argmin_{\tilde{\mathbf{S}}}||\mathcal{A}(\mathbf{S})-\widehat{\mathbf{Y}}||_2^2 +\lambda_1~||{\mathcal{P}_{\Theta}(\mathbf{S})}||_2^2+\lambda_2~||{\mathbf{S}}||_{TV}, ~~~~~~~~~~~~~[1] $$ where $$\mathcal{P}_{\Theta}(\mathbf{S})~=~{\mathcal{D}_{\Theta}(\mathbf{S})~-~\mathbf{S}}$$

Here, $$$\mathbf{S}$$$ is the joint set of DWIs, $$$\widehat{\mathbf{Y}}$$$ is the multi-channel k-space measurements and $$${\mathcal{A}({\mathbf{S}})}$$$ is the multi-channel encoding operator with phase compensation. $$${\mathcal{D}_{\Theta}(\mathbf{S})}$$$ is the learned representation of the q-space manifold and $$${\mathcal{P}_{\Theta}(\mathbf{S})}$$$ is the projection error to the q-space manifold. The manifold prior provides a voxel-wise projection of the current estimate to the q-space manifold. This error in the projection is minimized subject to data consistency to the measured samples. Additional image domain prior is imposed using of total variation (TV) regularization.

We tested the proposed method using a multi-shell in-vivo experiment. Fully-sampled data were collected using a 4-shot EPI trajectory from 3 b-shells: 1000, 2000 and 3000 s/mm2 with 60 points per shell ( 1.7mm isotropic, TE=58.3ms and partial Fourier: 71%). The data was incoherently under-sampled for R=4, 8, retrospectively. At R=4, only one random k-space shot is used per q-space point, with all 180 q-space points sampled. At R=8, 90 of the q-space points are left unsampled. We show reconstruction of all the 180 DWIs using the proposed method. We also show microstructural studies performed on the above data using the NODDI⁴ model.

Results

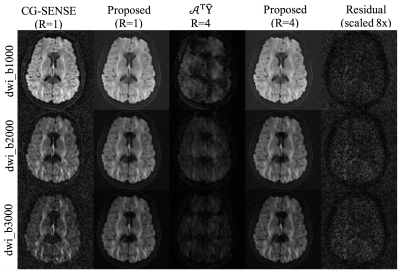
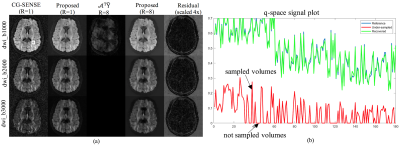
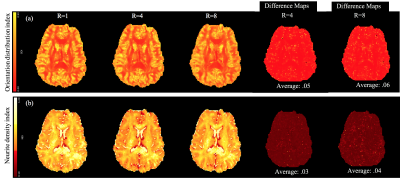
Figure 2 shows the reconstruction for R=4 for three test DWIs from each shell. For comparison, the reconstruction using the fully sampled data are also given along with the residual error in the proposed reconstruction. Figure 3 shows similar results for R=8. Here, a q-space signal plot is also included which shows the recovery of the missing volumes in q-space. Figure 4 shows the microstructural parameters fitted using the NODDI model on the fully sampled and the accelerated cases.

Discussion

The reconstructed DWIs and the microstructural measures at R=4,8 shows minimal artifacts compared to the fully sampled case, confirming the utility of the proposed joint reconstruction method. Further accelerations can be achieved in combination with multi-band imaging.

Conclusion

The proposed method provides a novel acceleration and reconstruction strategy to make use of msEPI for multi-shell dMRI studies. The reduced voxel sizes and the extensive q-space measurements together are expected to provide improved accuracy to microstructural studies, while the reduced scan-time enables practical utility.

Acknowledgements

Financial support for this study was provided by grants NIH 5 R01 EB022019, 5 R01 MH111578 and NIH 1R01EB019961-01A1. This work was conducted on MRI instruments funded by 1S10OD025025-01 and 1S10RR028821-01.