0107
Universal Sampling Denoising (USD) for noise mapping and noise removal of non-Cartesian MRI1New York University School of Medicine, New York, NY, United States
Synopsis
Non-Cartesian MRI enables efficient coverage in k-space and is leveraged to accelerate acquisitions of images in multiple contrasts. However, denoising such data is non-trivial, since the noise statistics is neither independent nor normally distributed in reconstructed images. Here, we propose a random-matrix-theory-based denoising and noise-mapping pipeline applicable to MRI of any non-Cartesian k-space sampling. We demonstrate the denoising pipeline on diffusion MRI data, including a numerical phantom and ex vivo mouse brain data in radial trajectories. The proposed pipeline robustly estimates the noise level, removes the noise, and corrects the bias in parametric maps of diffusion and kurtosis metrics.
Introduction
Non-Cartesian sampling in k-space provides flexibility in MRI acquisitions, e.g., for echo time (TE) shortening or motion robustness. Noise level estimation and noise removal are essential for image reconstruction and quantitative analysis, especially when images of multiple contrasts are acquired within limited scan time; however, denoising non-Cartesian sampled MRI is not as straightforward as for conventional Cartesian sampled data$$$\,$$$[1,2] due to the additional interpolation of non-uniformly sampled Fourier data onto a Cartesian grid in the reconstruction. Here, to estimate and remove noise for any sampling scene, we propose the first universal pipeline to simultaneously homogenize the noise level (i.e., variance stabilization) and de-correlate the noise in the gridded k-space and image space, such that the well-established Marchenko-Pastur principle-component-analysis (MP-PCA)$$$\,$$$[1,2,3] can be applied to identify and remove the noise. We demonstrate the pipeline in radially sampled diffusion MRI (dMRI) data in numerical phantoms and ex vivo mouse brain.Theory
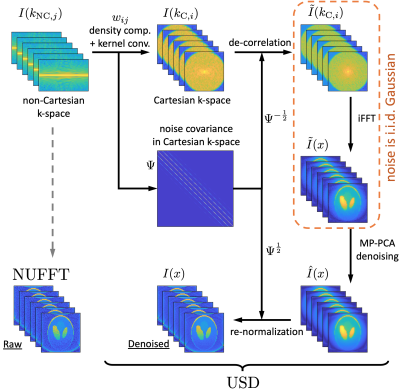
The denoising pipeline is summarized in Figure 1. Conventionally, the gridding operation includes four steps [4]: i) density compensation, ii) convolution with interpolation kernel in k-space (Kaiser-Bessel function $$$C(k)$$$), iii) inverse fast-Fourier-transform (iFFT), and iv) deapodization in image space. To simplify, the first two steps of gridding operation can be considered as a linear transformation:$$I(k_{\text{C},i})=\sum_j{}w_{ij}\cdot{}I(k_{\text{NC},j})\,,\quad(1)$$
where $$$I(k_{\text{C},i})$$$ and $$$I(k_{\text{NC},j})$$$ are k-space data on Cartesian grids and non-Cartesian trajectories, and $$$w_{ij}$$$ is the weights incorporating density compensation and kernel convolution.
The noise $$$\varepsilon(k_{\text{NC},j})$$$ on the non-Cartesian scan trajectory is independent and identically distributed (i.i.d.). However, the noise $$$\varepsilon(k_{\text{C},i})$$$ on a Cartesian grid after gridding operation is correlated through the linear relation in Eq.$$$\,$$$(1)$$$\,$$$[5]:
$$\langle\varepsilon(k_{\text{C},i})\varepsilon(k_{\text{C},i'})\rangle=\hat{\sigma}^{\,\,2}\cdot\Psi_{ii'}\,,\quad\Psi_{ii'}\equiv\sum_j{}w_{ij}w_{i'j}\,,$$
with $$$\hat{\sigma}$$$ the noise level. The key observation is the noise covariance matrix $$$\Psi_{ii'}$$$ on the k-space Cartesian grid is determined by the weighting coefficients $$$w_{ij}$$$. With the knowledge of noise correlation, the k-space data on the Cartesian grid can be de-correlated by using
$$\tilde{I}(k_{C,i})=\sum_{i'}\Psi^{-1/2}_{ii'}\cdot{}I(k_{C,i'})\,.$$
Given that the noise of de-correlated k-space data $$$\tilde{I}(k_{C,i})$$$ is roughly i.i.d., the noise statistics in its iFFT $$$\tilde{I}(x)$$$ is also i.i.d.. Remarkably, though the signal contrast in the noise de-correlated image $$$\tilde{I}(x)$$$ is very different from that of the ground truth, its noise statistics make it particularly suitable for applying random-matrix-theory-based noise removal pipeline. MP-PCA is then applied to estimate the noise level and the number $$$P(x)$$$ of signal components in PCA domain around voxel $$$x$$$, and remove the noise [1,2]. The noise components are removed by using the optimal shrinkage of singular values of PCA [3]. Finally the denoised image $$$\hat{I}(x)$$$ is re-normalized to recover its original contrast:
$${I}(x)=\frac{1}{c(x)}\text{FFT}\left\{\Psi^{1/2}\cdot\text{iFFT}\left\{\hat{I}(x)\right\}\right\}\,,$$
where $$$c(x)$$$ is the FT of convolution kernel $$$C(k)$$$ for deapodization. Similarly, the noise map $$$\hat{\sigma}(x)$$$ of de-correlated image $$$\tilde{I}(x)$$$ can be translated into the noise map $$$\sigma(x)$$$ of re-normalized image $$$I(x)$$$ via
$$\sigma^2(x)=\frac{1}{c(x)}\text{FFT}\left\{\Psi^{1/2}\cdot\hat{\sigma}^{\,\,2}(x)\right\}\,.$$
The above denoising pipeline is applicable to MRI data acquired with any k-space trajectories and dubbed as Universal Sampling Denoising (USD).
Method
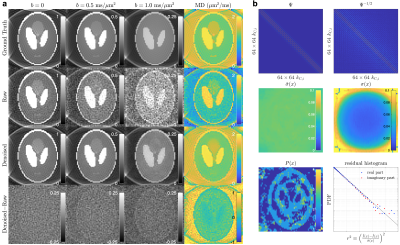
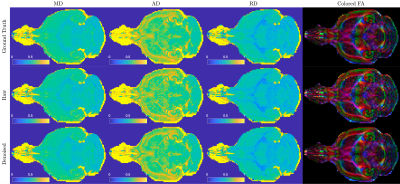
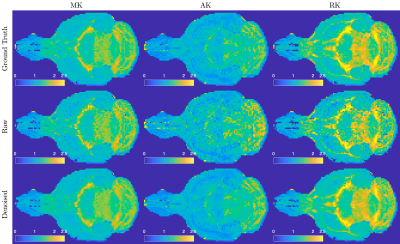
To demonstrate USD in simulated data, we created a 2-dimensional Shepp-Logan phantom of size 64$$$\times$$$64$$$\times$$$1, including a non-diffusion-weighted-image (non-DWI) $$$S_0$$$ and 30 DWIs of b-value $$$b$$$=0.1-1ms/μm2 with four different coils. The DWI signal was $$$S=S_0\cdot{}e^{-b\cdot{}D}$$$ with a diffusivity map $$$D=|6S_0-4S_0^2|$$$. Its k-space data was sampled on radial trajectories, consisting of 100 spokes/image and 128 sampled data points/spoke. The Gaussian noise of $$$\hat{\sigma}=0.05\cdot\sqrt{2}$$$ was added in k-space data on radial trajectories.Further, we demonstrated USD in dMRI data of an ex vivo mouse brain controlled at 25°C during scans. Diffusion measurements were performed on a mouse brain using a monopolar pulsed-gradient 2-dimensional radial acquisition $$$\,$$$[6] on a 7T Bruker scanner with a 4-channel cryocoil.$$$\,$$$The$$$\,$$$4$$$\,$$$channels$$$\,$$$provided$$$\,$$$extra$$$\,$$$data$$$\,$$$redundancy$$$\,$$$for$$$\,$$$noise$$$\,$$$removal,$$$\,$$$and$$$\,$$$were$$$\,$$$adaptive$$$\,$$$combined$$$\,$$$after$$$\,$$$denoising. We obtained 4 non-DWIs and 60 DWIs of b-value=[1,2]ms/μm2 along 30 directions per b-shell, with a resolution=0.156×0.156×1mm2, FOV=20×20mm2, and fixed TE/TR=20/400ms. The ground truth image was reconstructed from 402 center-out radial spokes with 70 data points/spoke by using non-uniform FFT (NUFFT) toolbox$$$\,$$$[7], and averaged over two repeated measurements. Instead, the noisy raw data was reconstructed from only 201 spokes without averaging over repeats. The USD denoising pipeline was applied to noisy raw data. Diffusion kurtosis imaging (DKI) [8] was fitted to the ground truth, raw data, and denoised data to calculate diffusion and kurtosis metrics: mean/axial/radial diffusivity/kurtosis (AD/RD/MD/AK/RK/MK) and colored fractional anisotropy (FA).
Result
In the numerical phantom, USD successfully removed noise and recovered the true values from the biased diffusivity values in noisy raw data (Figure 2a). The noise map is smooth, and the number of signal components in PCA domain is low, indicating the applicability of USD in simulations (Figure 2b).In mouse brain data, USD removed the noise in DWIs (Figure 3) and corrected the bias in parametric maps, especially in colored FA/MK/AK/RK maps (Figures 4-5). The$$$\,$$$signal-to-noise$$$\,$$$ratio$$$\,$$$(SNR)$$$\,$$$was$$$\,$$$increased$$$\,$$$by$$$\,$$$a$$$\,$$$factor$$$\,$$$of$$$\,$$$2$$$\,$$$after$$$\,$$$denoising.$$$\,$$$The$$$\,$$$slight$$$\,$$$decrease$$$\,$$$in$$$\,$$$structural$$$\,$$$details,$$$\,$$$$$$\,$$$compared$$$\,$$$with$$$\,$$$the$$$\,$$$ground$$$\,$$$truth$$$\,$$$(402$$$\,$$$spokes/image),$$$\,$$$was$$$\,$$$due$$$\,$$$to$$$\,$$$the$$$\,$$$sub-sampling$$$\,$$$in$$$\,$$$raw$$$\,$$$and$$$\,$$$denoised$$$\,$$$data$$$\,$$$(201$$$\,$$$spokes/image).$$$\,$$$For$$$\,$$$quantitative$$$\,$$$analysis$$$\,$$$(Figure$$$\,$$$3),$$$\,$$$the$$$\,$$$histogram$$$\,$$$of$$$\,$$$image$$$\,$$$residual$$$\,$$$$$$r\equiv[\tilde{I}(x)-\hat{I}(x)]/\hat{\sigma}(x)$$$$$$\,$$$showed$$$\,$$$that$$$\,$$$the$$$\,$$$noise$$$\,$$$removed$$$\,$$$by$$$\,$$$USD$$$\,$$$was$$$\,$$$normally$$$\,$$$distributed$$$\,$$$up$$$\,$$$to$$$\,$$$3$$$\,$$$standard$$$\,$$$deviations,$$$\,$$$and$$$\,$$$its$$$\,$$$curve$$$\,$$$in$$$\,$$$the$$$\,$$$semi-log$$$\,$$$scale$$$\,$$$was$$$\,$$$below$$$\,$$$the$$$\,$$$reference$$$\,$$$line$$$\,$$$of$$$\,$$$slope$$$\,$$$-1/2$$$\,$$$(PDF$$$\sim{}e^{-r^2/2}$$$),$$$\,$$$indicating$$$\,$$$that$$$\,$$$USD$$$\,$$$only$$$\,$$$removed$$$\,$$$noise$$$\,$$$without$$$\,$$$corrupting$$$\,$$$signals.$$$\,$$$This$$$\,$$$was$$$\,$$$also$$$\,$$$supported$$$\,$$$by$$$\,$$$the$$$\,$$$absence$$$\,$$$of$$$\,$$$anatomical$$$\,$$$structure$$$\,$$$in$$$\,$$$image$$$\,$$$residual$$$\,$$$map.
Conclusion and discussion
The USD pipeline successfully estimates the noise level and removes noise in non-Cartesian acquired data in a numerical phantom and dMRI data of an ex vivo mouse brain. Though tested only in 2d radially sampled MRI, the USD pipeline is applicable to noise removal of MRI/CT/PET data acquired in any 2d/3d k-space/projection-space sampling scene, as long as sufficiently data redundancy is presented (empirically ≥30 images). The USD pipeline can be either applied before the image reconstruction or incorporated as part of it, facilitating the data$$$\,$$$under-sampling$$$\,$$$and$$$\,$$$fast$$$\,$$$imaging$$$\,$$$in$$$\,$$$future$$$\,$$$study$$$\,$$$[9].Acknowledgements
We would like to thank Sungheon Gene Kim and Jin Zhang for sharing the code and experience of the image reconstruction, and Gregory Lemberskiy for the code and fruitful discussion of the coil-level random-matrix-theory denoising algorithm. This work was supported by the NIH under awards number R01 NS088040 (NINDS), R01 NS102904 (NINDS), and R01 EB027075 (NIBIB) by the Center of Advanced Imaging Innovation and Research (CAI2R, www.cai2r.net), a NIBIB Biomedical Technology Resource Center: P41 EB017183.
References
1. Veraart, J., Novikov, D. S., Christiaens, D., Ades-Aron, B., Sijbers, J., & Fieremans, E. (2016). Denoising of diffusion MRI using random matrix theory. Neuroimage, 142, 394-406.
2. Veraart, J., Fieremans, E., & Novikov, D. S. (2016). Diffusion MRI noise mapping using random matrix theory. Magnetic resonance in medicine, 76(5), 1582-1593.
3. Gavish, M., & Donoho, D. L. (2017). Optimal shrinkage of singular values. IEEE Transactions on Information Theory, 63(4), 2137-2152.
4. Jackson, J. I., Meyer, C. H., Nishimura, D. G., & Macovski, A. (1991). Selection of a convolution function for Fourier inversion using gridding (computerised tomography application). IEEE transactions on medical imaging, 10(3), 473-478.
5. Sengupta, A. M., & Mitra, P. P. (1999). Distributions of singular values for some random matrices. Physical Review E, 60(3), 3389.
6. Pauly, J. M., Conolly, S. I., Nishimura, D., the & Macovski, A. Slice-selective excitation for very short T2 species. Proc 8th Annual Meeting ISMRM, Amsterdam; 1989 (abstract 28).
7. Fessler, J. A. (2007). On NUFFT-based gridding for non-Cartesian MRI. Journal of magnetic resonance, 188(2), 191-195.
8. Jensen, J. H., Helpern, J. A., Ramani, A., Lu, H., & Kaczynski, K. (2005). Diffusional kurtosis imaging: the quantification of non‐gaussian water diffusion by means of magnetic resonance imaging. Magnetic Resonance in Medicine, 53(6), 1432-1440.
9. Lemberskiy, G., Baete, S., Veraart, J., Shepherd, T. M., Fieremans, E., & Novikov. D. S. (2019) Achieving sub-mm clinical diffusion MRI resolution by removing noise during reconstruction using random matrix theory. Proc 27th Annual meeting ISMRM, Montreal; 2019 (abstract 0770).
Figures