0105

Nonparametric 6D D-R₁-R₂ distribution imaging of the human brain: Initial results on healthy volunteers

Jan Martin¹, Alexis Reymbaut², Michael Uder³, Frederik Bernd Laun³, and Daniel Topgaard¹
¹Lund University, Lund, Sweden, ²Random Walk Imaging AB, Lund, Sweden, ³Institute of Radiology, University Hospital Erlangen, Friedrich-Alexander-Universität Erlangen-Nürnberg (FAU), Erlangen, Germany

Synopsis

Diffusion-relaxation correlation NMR methods have recently received attention from the medical MRI community for their ability to characterize microstructure and local chemical composition in complex tissues containing multiple subvoxel pools of water. We here implement 6D $$$\bf{D}$$$-$$$R_1$$$-$$$R_2$$$ distribution imaging of the human brain using a 20-min acquisition protocol combining EPI signal read-out and tensor-valued diffusion encoding with varying repetition- and echo times. Monte Carlo data inversion yields nonparametric distributions, statistical descriptors, and orientation-resolved diffusion and relaxation properties of white matter fiber bundles that are in good agreement with previous results from less exhaustive 4D and 5D protocols.

Introduction

Diffusion-relaxation correlation NMR^1-5 resolves information on the translational motion of water molecules and the local chemical composition of the aqueous phase. Recently, these methods were combined with spatially resolved measurements^6-8 and applied in vivo using data analysis with model-based^9-12 and nonparametric approaches^13,14. However, early nonparametric studies were limited to scalar diffusivity measures, which are not satisfactory for orientationally disordered anisotropic materials.

We have incorporated the concepts of diffusion tensor distributions^15-17, tensor-valued encoding^18-20, and Monte Carlo inversion^21,22 into the framework of diffusion-relaxation correlation NMR. Mapping statistical descriptors of these distributions onto orientation distribution functions (ODFs) allows resolving fiber-specific subvoxel components. Building on experiences from previous 5D $$$\bf{D}$$$-$$$R_1$$$ and $$$\bf{D}$$$-$$$R_2$$$ in vivo studies^23,24, we here adapt our 6D$$$\bf{D}$$$-$$$R_1$$$-$$$R_2$$$ NMR spectroscopy method²⁵ to a 20-min in vivo acquisition protocol and perform proof-of-principle brain imaging on healthy volunteers.

Methods

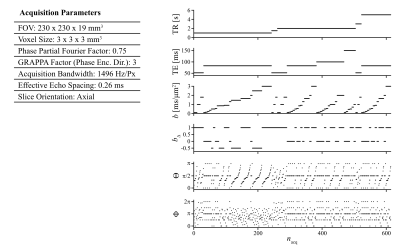
The study was approved by the local institutional review board. Three healthy volunteers were measured on a 3T system (MAGNETOM Prisma, Siemens Healthcare AG, Erlangen, Germany) with a 20-channel head coil. Data were acquired using an in-house developed single-shot spin-echo EPI sequence modified for tensor-valued diffusion encoding²⁶. Numerically optimized²⁷ linear, planar, and spherical b-tensors were employed with b-values ranging between 0.1 and 3 ms/mm². Sensitivity to $$$R_1$$$ and $$$R_2$$$ was achieved by acquiring data with different combinations of repetition- and echo times. Total protocol duration was 20 min. Figure 1 provides a detailed overview of acquisition parameters.

The data were subsequently processed in Matlab R2019b (MathWorks, Natick, MA) using the 6D Monte Carlo inversion algorithm²⁵ as implemented in the multidimensional diffusion MRI toolbox²⁸ available at https://github.com/daniel-topgaard/md-dmri (last accessed November 23^rd, 2020). The components of the inversion, i.e. axial diffusivity $$$D_{||}$$$, radial diffusivity $$$D_{\bot}$$$, azimuthal angle $$$\Theta$$$, polar angle $$$\Phi$$$, longitudinal relaxation rate $$$R_1$$$, and transversal relaxation rate $$$R_2$$$, were sampled in the following ranges: $$$D_{||},D_\bot\in\left[0.05,5\right]$$$ μm²/ms, $$$\Theta\in [0,π)$$$, $$$\Phi\in [0,2π)$$$, $$$R_1\in [0.2,1]$$$ s^-1, $$$R_2\in [1,30]$$$ s^-1. Following the nomenclature in ²⁵ we employed $$$N_{in}=200$$$ input components, $$$N_{p}=20$$$ proliferation steps, $$$N_{m}=20$$$ mutation steps, and $$$N_{out}=10$$$ output components. For each voxel, $$$N_{bs}=100$$$ plausible solutions were obtained by way of bootstrapping with replacement.

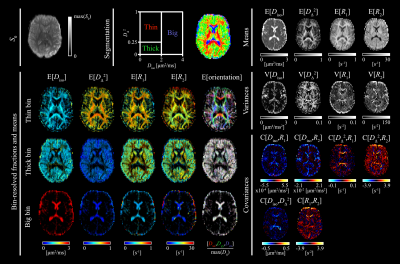
We quantified our results in terms of the median across all bootstraps. For the sake of simplicity, the median operator is omitted and the mean, variance, and covariance of two given components $$$x,y$$$ are denoted as $$$\mathrm{E}[x]$$$, $$$\mathrm{V}[x]$$$, and $$$\mathrm{C}[x, y]$$$, respectively. The 6D parameter space was separated into three bins to obtain tissue-specific statistical descriptors²³. The bin dimensions are shown in Figure 3 and were chosen to effectively isolate white matter (WM, "thin"), gray matter (GM, "thick"), and cerebrospinal fluid (CSF, "big"). Besides $$$D_{||}$$$ and $$$D_\bot$$$, we also characterize $$$\bf{D}$$$ in terms of its isotropic diffusivity $$$D_{iso}=(D_{||}+2D_\bot)/3$$$ and normalized anisotropy $$$D_\Delta=(D_{||}-D_\bot)/D_{iso}$$$²⁹.

ODFs were computed for the thin-bin fraction of the bootstrap solutions by mapping the orientation specific mean $$$Ê[x]$$$ onto a dense spherical mesh grid³⁰. The ODF radii represent the thin-bin components' weight and orientation.

Results

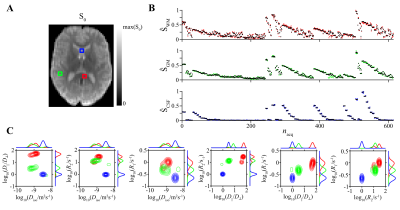
Figure 2 shows experimental and fitted signals and corresponding distributions $$$\mathcal{P}(\bf{D}\it,R_1,R_2)$$$ in three representative voxels associated with WM in the corpus callosum, cortical GM, and CSF in the frontal ventricles. The parameter distributions reflect familiar aspects of the respective tissue type: $$$D_{||}/D_\bot$$$ is high in WM but low in GM and CSF. WM and GM have similar $$$D_{iso}$$$, while $$$D_{iso}$$$ in CSF is notably higher. $$$R_1$$$ and $$$R_2$$$ are lowest in CSF, followed by GM, and highest in WM.

Figure 3 displays axial maps of global and bin-specific statistical descriptors of $$$\mathcal{P}(\bf{D}\it,R_1,R_2)$$$. Maps of the mean values are consistent with the distributions shown in Figure 2. The contrasts are in good agreement with previously published data that were analyzed with 4D and 5D Monte Carlo inversion algorithms^23,24,31.

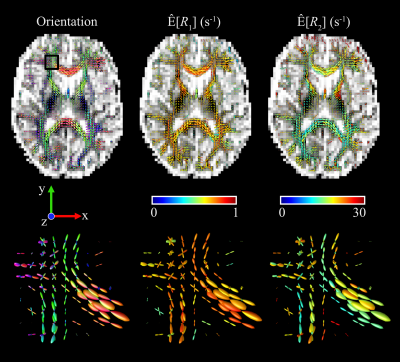
Figure 4 presents thin-bin ODFs with color-coding based on orientation, $$$Ê[R_1]$$$, and $$$Ê[R_2]$$$ for a representative axial slice. Local orientations captured in the ODFs are consistent with known anatomy. In both $$$Ê[R_1]$$$ and $$$Ê[R_2]$$$ gradual changes are noticeable at interfaces between WM and either CSF or GM, as well as between the genu and splenium of the corpus callosum.

Discussion

In this work we demonstrated that 6D $$$\bf{D}$$$-$$$R_1$$$-$$$R_2$$$ MRI is feasible on a clinical system using a single 20-min acquisition protocol that is comparable to previous 5D $$$\bf{D}$$$-$$$R_1$$$ (20 min) and $$$\bf{D}$$$-$$$R_2$$$ (15 or 45 min) measurements^23,24. However, advanced contrasts such as variances and covariances require careful optimization of the acquisition protocol. We consciously neglected the possibly confounding impact of eddy current³² and diffusion time dependence^33,34 in favor of a broader sampling space to stabilize the nonparametric Monte Carlo inversion. Limited by the design of the sequence we were only able to acquire five slices. More efficient acquisition schemes are possible with advanced sequence designs such as slice shuffling^35,36. Further improvements include pre-processing steps such as denoising^37,38 and correcting for Rician bias^39,40. Nonetheless, our results show that 6D $$$\bf{D}$$$-$$$R_1$$$-$$$R_2$$$ MRI provides abundant information on subvoxel tissue microstructure that may benefit clinical MRI in the future.

Acknowledgements

This work was financially supported by the Swedish Foundation for Strategic Research (ITM17-0267) and the Swedish Research Council (2018-03697). D. Topgaard owns shares in Random Walk Imaging AB (Lund, Sweden, http://www.rwi.se/), holding patents related to the described methods.

Funding for the position of F. B. Laun by the DFG is gratefully acknowledged (LA 2804/12-1). We thank the Imaging Science Institute (Erlangen, Germany) for providing us with measurement time.

References

¹Galvosas, P. and P.T. Callaghan, Multi-dimensional inverse Laplace spectroscopy in the NMR of porous media. Comptes Rendus Physique, 2010. 11(2): p. 172-180

² Bernin, D. and D. Topgaard, NMR diffusion and relaxation correlation methods: New insights in heterogeneous materials. Current Opinion in Colloid & Interface Science, 2013. 18(3): p. 166-172

³ Song, Y.-Q., et al., Chapter 4: Two-dimensional NMR of Diffusion and Relaxation, in Diffusion NMR of Confined Systems: Fluid Transport in Porous Solids and Heterogeneous Materials. 2017, The Royal Society of Chemistry. p. 111-155

⁴ Tax, C.M., Estimating Chemical and Microstructural Heterogeneity by Correlating Relaxation and Diffusion. Advanced Diffusion Encoding Methods in MRI, 2020. 24: p. 186

⁵ Benjamini, D. and P.J. Basser, Multidimensional correlation MRI. NMR in Biomedicine, 2020. 33(12): p. e4226

⁶ Zhang, Y. and B. Blümich, Spatially resolved D–T2 correlation NMR of porous media. Journal of Magnetic Resonance, 2014. 242: p. 41-48

⁷ Kim, D., et al., Diffusion-relaxation correlation spectroscopic imaging: A multidimensional approach for probing microstructure. Magnetic Resonance in Medicine, 2017. 78(6): p. 2236-2249

⁸ Benjamini, D. and P.J. Basser, Magnetic resonance microdynamic imaging reveals distinct tissue microenvironments. NeuroImage, 2017. 163: p. 183-196

⁹ De Santis, S., et al., T1 relaxometry of crossing fibres in the human brain. NeuroImage, 2016. 141: p. 133-142

¹⁰ De Santis, S., et al., Resolving relaxometry and diffusion properties within the same voxel in the presence of crossing fibres by combining inversion recovery and diffusion-weighted acquisitions. Magnetic Resonance in Medicine, 2016. 75(1): p. 372-380

¹¹ Veraart, J., D.S. Novikov, and E. Fieremans, TE dependent Diffusion Imaging (TEdDI) distinguishes between compartmental T2 relaxation times. NeuroImage, 2018. 182: p. 360-369

¹² Veraart, J., et al., Model-based Analysis of Advanced Diffusion Data. Advanced Diffusion Encoding Methods in MRI, 2020. 24: p. 317

¹³ Slator, P.J., et al., Combined diffusion-relaxometry MRI to identify dysfunction in the human placenta. Magnetic Resonance in Medicine, 2019. 82(1): p. 95-106

¹⁴ Benjamini, D., Nonparametric Inversion of Relaxation and Diffusion Correlation Data. Advanced Diffusion Encoding Methods in MRI, 2020. 24: p. 278.

¹⁵ Basser, P.J. and S. Pajevic, A normal distribution for tensor-valued random variables: applications to diffusion tensor MRI. IEEE Transactions on Medical Imaging, 2003. 22(7): p. 785-794

¹⁶ Jian, B., et al., A novel tensor distribution model for the diffusion-weighted MR signal. NeuroImage, 2007. 37(1): p. 164-176

¹⁷ Topgaard, D., Diffusion tensor distribution imaging. NMR in Biomedicine, 2019. 32(5): p. e4066

¹⁸ Westin, C.-F., et al. Measurement Tensors in Diffusion MRI: Generalizing the Concept of Diffusion Encoding. 2014. Cham: Springer International Publishing

¹⁹ Topgaard, D., Multidimensional diffusion MRI. Journal of Magnetic Resonance, 2017. 275: p. 98-113

²⁰ Reymbaut, A., Diffusion Anisotropy and Tensor-valued Encoding. Advanced Diffusion Encoding Methods in MRI, 2020. 4: p. 68

²¹ Prange, M. and Y.-Q. Song, Quantifying uncertainty in NMR T2 spectra using Monte Carlo inversion. Journal of Magnetic Resonance, 2009. 196(1): p. 54-60

²² de Kort, D.W., et al., NMR Nanoparticle Diffusometry in Hydrogels: Enhancing Sensitivity and Selectivity. Analytical Chemistry, 2014. 86(18): p. 9229-9235

²³ de Almeida Martins, J.P., et al., Transferring principles of solid-state and Laplace NMR to the field of in vivo brain MRI. Magn. Reson., 2020. 1(1): p. 27-43

²⁴ Reymbaut, A., et al., Towards non-parametric diffusion-T1 characterization of crossing fibers in the human brain. arXiv:2006.07881, 2020

²⁵ de Almeida Martins, J.P. and D. Topgaard, Multidimensional correlation of nuclear relaxation rates and diffusion tensors for model-free investigations of heterogeneous anisotropic porous materials. Scientific Reports, 2018. 8(1): p. 2488

²⁶ Martin, J., et al., Contrast-to-noise ratio analysis of microscopic diffusion anisotropy indices in q-space trajectory imaging. Zeitschrift für Medizinische Physik, 2020. 30(1): p. 4-16

²⁷ Sjölund, J., et al., Constrained optimization of gradient waveforms for generalized diffusion encoding. Journal of Magnetic Resonance, 2015. 261: p. 157-168

²⁸ Nilsson, M., et al. An open-source framework for analysis of multidimensional diffusion MRI data implemented in MATLAB. in Proc Intl Soc Mag Reson Med. 2018

²⁹ Conturo, T.E., et al., Encoding of anisotropic diffusion with tetrahedral gradients: A general mathematical diffusion formalism and experimental results. Magnetic Resonance in Medicine, 1996. 35(3): p. 399-412

³⁰de Almeida Martins, J.P., et al., Computing and visualising intra-voxel orientation-specific relaxation–diffusion features in the human brain. Human Brain Mapping

³¹ Yon, M., et al., Diffusion tensor distribution imaging of an in vivo mouse brain at ultrahigh magnetic field by spatiotemporal encoding. NMR in Biomedicine, 2020. 33(11): p. e4355

³² Yang, G. and J.A. McNab, Eddy current nulled constrained optimization of isotropic diffusion encoding gradient waveforms. Magnetic Resonance in Medicine, 2019. 81(3): p. 1818-1832

³³ Baron, C.A. and C. Beaulieu, Oscillating gradient spin-echo (OGSE) diffusion tensor imaging of the human brain. Magnetic Resonance in Medicine, 2014. 72(3): p. 726-736

³⁴ Arbabi, A., et al., Diffusion dispersion imaging: Mapping oscillating gradient spin-echo frequency dependence in the human brain. Magnetic Resonance in Medicine, 2020. 83(6): p. 2197-2208

³⁵ Hutter, J., et al., Integrated and efficient diffusion-relaxometry using ZEBRA. Scientific Reports, 2018. 8(1): p. 15138

³⁶ Hutter, J., J.D. Tournier, and J. Hajnal, Chapter 9: Pulse Sequences Combining Advanced Diffusion Encoding and Image Read-out, in Advanced Diffusion Encoding Methods in MRI. 2020, The Royal Society of Chemistry. p. 249-277

³⁷ Veraart, J., et al., Denoising of diffusion MRI using random matrix theory. NeuroImage, 2016. 142: p. 394-406

³⁸ Cordero-Grande, L., et al., Complex diffusion-weighted image estimation via matrix recovery under general noise models. NeuroImage, 2019. 200: p. 391-404

³⁹ Gudbjartsson, H. and S. Patz, The rician distribution of noisy mri data. Magnetic Resonance in Medicine, 1995. 34(6): p. 910-914

⁴⁰ Koay, C.G. and P.J. Basser, Analytically exact correction scheme for signal extraction from noisy magnitude MR signals. Journal of Magnetic Resonance, 2006. 179(2): p. 317-322

⁴¹ Eriksson, S., et al., NMR diffusion-encoding with axial symmetry and variable anisotropy: Distinguishing between prolate and oblate microscopic diffusion tensors with unknown orientation distribution. The Journal of Chemical Physics, 2015. 142(10): p. 104201

Figures

Acquisition parameters and diffusion encoding scheme sorted by acquisition index $$$n_{acq}$$$. TR denotes the repetition time and TE denotes the echo time. Anisotropy of the b-tensor is represented by $$$b_\Delta$$$ where values of 1, 0, and -0.5 indicate linear, spherical, and planar b-tensors, respectively⁴¹. $$$\Theta$$$ and $$$\Phi$$$ denote the azimuthal and polar angle, respectively.

Experimental data in three representative voxels. (A) $$$S_0$$$ map with labeled voxels: WM in the corpus callosum (red), cortical GM (green), and CSF in the frontal ventricle (blue). (B) Normalized signal $$$S$$$ versus acquisition index $$$n_{acq}$$$ (measured: black, fitted: colors correspond to the selected voxels). (C) Selected 2D projections of the 6D $$$\bf{D}$$$-$$$R_1$$$-$$$R_2$$$ nonparametric distributions obtained by the Monte Carlo inversion.

Statistical descriptors derived from the 6D $$$\bf D$$$-$$$R_1$$$-$$$R_2$$$ distributions shown for a representative axial slice. Displayed are the median values of 100 per-bootstrap means $$$\mathrm{E}$$$, variances $$$\mathrm{V}$$$, and covariances $$$\mathrm{C}$$$. Bin-resolved fractions and means obtained by binning the parameter space to isolate WM ("thin"), GM ("thick"), and CSF ("big"). $$$\bf D$$$ is characterized in terms of the isotropic diffusivity $$$D_{iso} = (D_{||} + 2 D_\bot)/3$$$ and normalized anisotropy $$$D_\Delta = (D_{||} - D_\bot)/D_{iso}$$$.

Orientation-colored, $$$Ê[R_1]$$$-colored, and $$$Ê[R_2]$$$-colored ODFs calculated for the thin-bin fraction of a representative axial slice. $$$Ê$$$ denotes the orientation specific median across 100 per-bootstrap means. ODFs are overlaid over a $$$1-f_{thin}$$$ map of the signal where $$$f_{thin}$$$ denotes the thin-bin fraction. Magnified sections of crossing fibers (black square) are shown in the bottom row.

Proc. Intl. Soc. Mag. Reson. Med. 29 (2021)

0105