0071
Fourier-based decomposition approach for simultaneous acquisition of 1H spectra from two voxels in vivo at short echo times1Physikalisch-Technische Bundesanstalt (PTB), Braunschweig und Berlin, Germany, 2Center for Stroke Research Berlin, Charité Universitätsmedizin, Berlin, Germany, 3Center for Magnetic Resonance Research, University of Minnesota, Minneapolis, MN, United States
Synopsis
In this work, a Fourier-based technique for 1H MR spectroscopy based on split-slice-GRAPPA is introduced to decompose simultaneously acquired dual-voxel data. In contrast to the existing sensitivity-map-based approach, this technique does not need any additional image acquisitions. The autocalibration lines are derived by additional low SNR spectral data. 2SPECIAL was used to simultaneously acquire data from two voxels at short echo times. The proposed decomposition algorithm was first validated in a multi-compartment phantom, and its application was then demonstrated at 7T in vivo.
Introduction
In single-voxel spectroscopy (SVS), the advantage of an improved metabolite SNR and a more compact point spread function1 at short measurement times compared to MRSI is accompanied by the disadvantage of only measuring the signal of one limited region2.To address this issue, several methods for simultaneous multi-voxel spectroscopy (SMVS) measurements were proposed3–6 in the past years similar to the use of simultaneous multi-slice (SMS) in MR imaging7,8, which mostly use the explicit knowledge of coil sensitivities to retrospectively decompose the signal simultaneously acquired from two voxels.
In this work, we present a technique based on the split-slice GeneRalized Autocalibrating Partial Parallel Acquisition (split-slice GRAPPA)9,10 algorithm, called voxel-GRAPPA (vGRAPPA), to decompose the combined signal originating from two spatially distinct voxels obtained via SMVS without the need for additional coil sensitivities. For data acquisition, we use the 2 spin-echo full-intensity acquired localization (2SPECIAL) sequence to simultaneously excite two voxels in a multi-compartment phantom and in vivo. This approach is then compared to the SENSitivity Encoding (SENSE) based decomposition3,4.
Methods
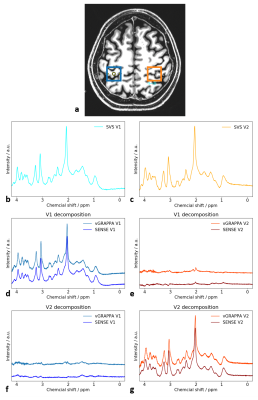
Data AcquisitionAll measurements were performed on a 7T scanner (Magnetom, Siemens Healthineers, Erlangen, Germany) using a 1Tx/32Rx head coil (NOVA Medical, Wilmington, USA). A phantom was composed of a 210-mm diameter sphere containing four spheres with a 50-mm diameter filled with 10mmol solutions of different metabolites (Fig.1a). One healthy volunteer was examined according to local ethics regulations. Spectra were obtained from the left and right motor cortex (Fig.2a).
The measurement protocol for phantom and in vivo measurements were as follows: MP2RAGE11 images were acquired for accurate positioning of the voxels and to determine coil sensitivity profiles. A MATLAB B0 Shimtool12,13 was adapted to obtain an optimized 2nd-order shim for both voxels simultaneously. The reference transmitter voltage for the SMVS acquisition was calculated by taking the mean voltage value for both single-voxel optimized reference voltages. First, single voxel spectra were acquired using a regular SPECIAL14,15 sequence for each voxel while keeping the same settings as for the SMVS acquisition. Then, the 2SPECIAL sequence6 was used to simultaneously acquire spectral data from both voxels. As with conventional SPECIAL, an interleaved water suppression16 and 3D outer volume saturation (OVS) scheme was applied before the adiabatic inversion, only a seventh OVS band was added to also saturate the volume between the two voxels. The following scan parameters were used for the two sequences: NA=32/64 (phantom/in vivo), TE/TR=9/7500ms, VOI=(20mm)³, data points=2048, acquisition bandwidth=4000Hz.
Spectral Reconstruction
Post-processing and decomposition of the signals using vGRAPPA and the SENSE-based decomposition were performed with in-house written tools in MATLAB-2019b and Python3.6. Metabolite concentrations from all resulting in vivo spectra were estimated using LCModel17.
vGRAPPA and SENSE-based Decomposition
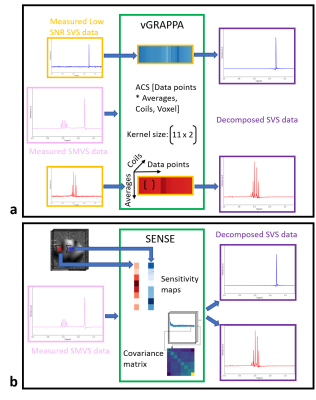
Both algorithms are illustrated in Fig.3 and were applied for both phantom and in vivo acquisitions.
First, four averages of SVS spectra were acquired for each voxel. This low SNR data was used to generate the vGRAPPA kernel. The required autocalibration signal (ACS) for each voxel was derived by rearranging the channel-wise low SNR datapoints and the averages (Fig.3a). The kernel size was chosen to be 11x2. The resulting kernel function was then used to decompose the SMVS data to their respective regions.
For the SENSE-based decomposition algorithm, the channel-wise coil sensitivities, as well as the noise covariance matrix, were derived from image data and spectral data, respectively (Fig.3b).
All spectra were post-processed by summation of the even and uneven averages for full localization, zero-filling by a factor of 2, weighted and phase-corrected coil combination, frequency correction, and averaging. The performance of both algorithms was assessed by treating both SVS datasets like the SMVS data and decomposing each of them to their respective regions.
Leakage Quantification
In phantom measurements, the signal leakage between voxels was quantified by integration of the respective leak signal – i.e. the signal visible in the spectrum of the other voxel – which was then normalized to the signal of the same metabolite in the voxel the signal is originating from.
Results and Discussion
Both SENSE-based and vGRAPPA decomposition allow the assignment of the SMVS signal to their respective regions with signal leakage below 6% (Fig.1b-d). vGRAPPA results in a mean leakage of 3.4%, while the SENSE-based decomposition results in a slightly increased leakage of 5.0%.The spectral shape of the SENSE- and vGRAPPA-decomposed in vivo spectra of both voxels is similar to the one obtained by SVS acquisition (Fig.2b-d,g). The signal of the respective other voxel shows a small signal with frequency-dependent peaks that exceed the noise level for both decomposition algorithms (Fig.2e-f).
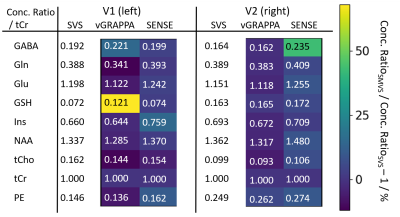
Results from in vivo metabolite quantification for all spectra are shown in Tab.1. The overall deviation from the SVS measurements averaged over both voxels and the 9 quantified metabolites are 4.8% and 5.4% for the vGRAPPA and the SENSE-based approach, respectively. These deviations can be partially attributed to imperfections of the applied decomposition technique.
Conclusion
The proposed vGRAPPA algorithm for decomposition of two simultaneously acquired voxels to their respective regions was successfully validated in phantom and in vivo measurements. Although high-quality spectra were obtained for both the vGRAPPA and the SENSE-based algorithm, the vGRAPPA method requires less computational power as no image data is needed and is thus less time-consuming.Acknowledgements
We would like to thank Steen Moeller, University of Minnesota, USA, for providing the split-slice GRAPPA code. This project has received funding from the EMPIR program co-financed by the Participating States and from the European Union’s Horizon 2020 researchand innovation program. This paper reflects only the author's view and EURAMET is not responsible for any use that may be made of the information itcontains. Furthermore this project received funding from grant number IT7/8-1 of the DFG.References
1. Skoch A, Jiru F, Bunke J. Spectroscopic imaging: Basic principles. Eur J Radiol. 2008;67(2):230-239. doi:10.1016/j.ejrad.2008.03.003
2. Öz G, Deelchand DK, Wijnen JP, et al. Advanced single voxel 1H magnetic resonance spectroscopy techniques in humans: Experts’ consensus recommendations. NMR Biomed. 2020;(October 2019):1-18. doi:10.1002/nbm.4236
3. Boer VO, Klomp DWJ, Laterra J, Barker PB. Parallel reconstruction in accelerated multivoxel MR spectroscopy. Magn Reson Med. 2015;74(3):599-606. doi:10.1002/mrm.25718
4. Landheer K, Sahgal A, Das S, Graham SJ. Constrained source space MR spectroscopy: Multiple voxels, no gradient readout. Am J Neuroradiol. 2015;36(8):1436-1443. doi:10.3174/ajnr.A4319
5. Dehghani M, Edden R, Near J. Simultaneous ultra-short TE-MRS in two voxels using a SPECIAL sequence with Hadamard encoding. Proc 28th Annu Meet ISMRM,. 2020:0491.
6. Riemann LT, Aigner CS, Brühl R, et al. Adiabatic multiband inversion for simultaneous acquisition of 1H MR spectra from two voxels in-vivo at very short echo times. Proc 28th Annu Meet ISMRM,. 2020:0737.
7. Larkman DJ, Hajnal J V., Herlihy AH, Coutts GA, Young IR, Ehnholm G. Use of multicoil arrays for separation of signal from multiple slices simultaneously excited. J Magn Reson Imaging. 2001;13(2):313-317. doi:10.1002/1522-2586(200102)13:2<313::aid-jmri1045>3.3.co;2-n
8. Moeller S, Yacoub E, Olman CA, et al. Multiband multislice GE-EPI at 7 tesla, with 16-fold acceleration using partial parallel imaging with application to high spatial and temporal whole-brain FMRI. Magn Reson Med. 2010;63(5):1144-1153. doi:10.1002/mrm.22361
9. Cauley SF, Polimeni JR, Bhat H, Wald LL, Setsompop K. Interslice leakage artifact reduction technique for simultaneous multislice acquisitions. Magn Reson Med. 2014;72(1):93-102. doi:10.1002/mrm.24898
10. Schmitter S, Adriany G, Waks M, et al. Bilateral Multiband 4D Flow MRI of the Carotid Arteries at 7T. Magn Reson Med. 2020;84(4):1947-1960. doi:10.1002/mrm.28256
11. Marques JP, Kober T, Krueger G, van der Zwaag W, Van de Moortele PF, Gruetter R. MP2RAGE, a self bias-field corrected sequence for improved segmentation and T1-mapping at high field. Neuroimage. 2010;49(2):1271-1281. doi:10.1016/j.neuroimage.2009.10.002
12. Fillmer A, Kirchner T, Cameron D, Henning A. Constrained image-based B0 shimming accounting for “local minimum traps” in the optimization and field inhomogeneities outside the region of interest. Magn Reson Med. 2015;73(4):1370-1380. doi:10.1002/mrm.25248
13. Nassirpour S, Chang P, Fillmer A, Henning A. A comparison of optimization algorithms for localized in vivo B 0 shimming. Magn Reson Med. 2018;79(2):1145-1156. doi:10.1002/mrm.26758
14. Mlynárik V, Gambarota G, Frenkel H, Gruetter R. Localized short-echo-time proton MR spectroscopy with full signal-intensity acquisition. Magn Reson Med. 2006;56(5):965-970. doi:10.1002/mrm.21043
15. Mekle R, Mlynárik V, Gambarota G, Hergt M, Krueger G, Gruetter R. MR spectroscopy of the human brain with enhanced signal intensity at ultrashort echo times on a clinical platform at 3T and 7T. Magn Reson Med. 2009;61(6):1279-1285. doi:10.1002/mrm.21961
16. Tkáč I, Gruetter R. Methodology of 1H NMR spectroscopy of the human brain at very high magnetic fields. Appl Magn Reson. 2005;29(1):139-157. doi:10.1007/BF03166960
17. Provencher SW. Estimation of metabolite concentrations from localized in vivo proton NMR spectra. Magn Reson Med. 1993;30(6):672-679. doi:10.1002/mrm.1910300604
Figures