0069
Manifold learning via tangent space alignment for accelerated dynamic MR imaging with highly undersampled (k,t)-data1Gordon Center for Medical Imaging, Department of Radiology, Massachusetts General Hospital, Harvard Medical School, Boston, MA, United States, 2LTCI, Telecom Paris, Institut Polytechnique de Paris, Paris, France, 3LIP6, Sorbonne University, CNRS, Paris, France
Synopsis
Many unsupervised learning methods have been proposed to discover the structure of manifolds embedded in high-dimensional input spaces. However, image reconstruction requires mapping the learned low-dimension data in the feature space back to the input space, which can be challenging if the mapping function is implicit. This work presents an image reconstruction scheme closely related to machine learning methods learning manifolds via tangent space alignment. Here, the mapping transform is explicit and learned from the data. This model is a nonlinear generalization of the Low-Rank matrix/tensor model, reconstructing undersampled MR data with lower rank than the standard Low-Rank reconstruction.
Introduction
High-dimensional data often reside in a very low-dimensional nonlinear manifold, which can be exploited for image classification and reconstruction. Many unsupervised learning methods, such as locally linear embedding (LLE)1, Isomap2, Graph Laplacian3, etc., have been proposed to discover the structure of the manifold embedded in high-dimensional input spaces. These methods can be interpreted within a kernel principal component analysis (PCA) framework4, where an implicit mapping of the training data to a feature space is constructed while preserving some geometries of the training data. Different from image classification, where it is sufficient to perform the task in the feature space, manifold learning based-image reconstruction requires mapping the learned low-dimension data in the feature space back to the input space, aka, pre-imaging, which can be challenging if the kernel matrix is formed implicitly from the training data5. One way to avoid the pre-imaging problem is performing image reconstruction with a regularization term promoting the smoothness on manifolds that can be calculated in the input space6.This work presents an alternative strategy for manifold learning-based image reconstruction. The proposed method is closely related to machine learning methods that learn manifolds via tangent space alignment7, where the geometries of the manifold are learned locally but fitted globally by aligning the subspaces in each neighborhood. We validate the performance of the proposed method in dynamic MR with highly undersampled k-space data.
Method
Consider a dynamic image series $$$X=[x_1,...,x_N]\in{\mathbb{C}^{M\times{N}}}$$$ lying in a low-dimensional manifold $$$\mathcal{M}$$$ where $$$M$$$ is the number of voxels and $$$N$$$ the number of frames. Assume the images can be grouped into $$$C$$$ neighborhoods based on a certain similarity metric, i.e. $$$X_c=[x_{i^{(c)}_{1}},...,x_{i^{(c)}_{K_c}}]\in{\mathbb{C}^{M\times{K_c}}}$$$ where $$${i^{(c)}_{k}}$$$ corresponds to the frame index of the $$$k$$$-th image at the $$$c$$$-th neighborhood and $$$K_c$$$ to the total number of frame in that neighborhood. Note that the neighborhoods do not need to be distinct and can overlap. The local geometry of the manifold can be learned by constructing an approximation for the tangent space at the $$$c$$$-th neighborhood:$$X_c={\Theta}_c{\Phi}_c^T\qquad(1)$$
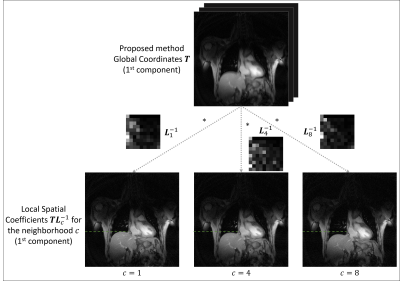
where $$${\Phi}_c\in{\mathbb{C}^{{K_c}\times{d}}}$$$ is a matrix forming an orthonormal basis of the subspace that can be learned from training data and $$${\Theta}_c\in{\mathbb{C}^{M\times{d}}}$$$ are the local coordinates of the manifold. We propose to construct the global coordinates $$$T=[{\tau}_1,...,{\tau}_d]\in{\mathbb{C}^{M\times{d}}}$$$ of the manifold (in an implicit feature space) by aligning the local coordinates $$${\Theta}_c$$$ via an affine model:
$$T={\Theta}_c{L_c}\qquad(2)$$
where $$$L_c\in{\mathbb{C}^{d\times{d}}}$$$ is an affine transformation matrix. Note that the images at each neighborhood (in the input space) can be explicitly represented by the global coordinates and thus avoiding the pre-imaging problem in the conventional kernel PCA:
$$X_c=T{L}_c^{-1}{\Phi}_c^T\qquad(3)$$
We can show that the above model is a nonlinear generalization of the low-rank matrix/tensor model8,9. Also note that the above model is different from the local low-rank model where the local coordinates are determined independently.
In image reconstruction, we seek to find $$$T$$$ and $$$L_c$$$ to minimize the representation error with a sparsity constraint on $$$T$$$:
$$arg\min_{T,\left\{{{L}_c}^{-1}\right\}_{c=1}^C}\frac{1}{2}\sum_{c=1}^C{||s_c-A_c\left\{T{L}_c^{-1}{\Phi}_c^T\right\}||_2^2}+{\lambda}_1||DT||_1+\frac{{\lambda}_2}{2}||T||_F^2\qquad(4)$$
where, $$$s_c$$$ is the undersampled k-space data in a neighborhood $$$c$$$, $$$A_c$$$ is the forward imaging matrix, $$$D$$$ is the finite difference operator along space, $$$\lambda_1$$$ and $$$\lambda_2$$$ are scaling parameters for the penalty terms.
We solve the optimization problem in equation (4) using the alternating direction methods of multipliers (ADMM) algorithm10.
Results
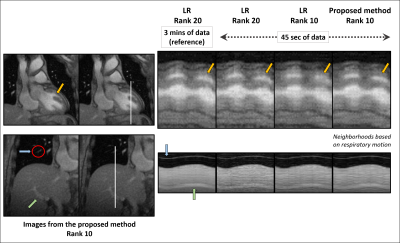
One healthy volunteer was imaged (approved by our local IRB) on a 3T MR scanner (Siemens Trio) for a 3-minute scan. The MR images were acquired using a GRE sequence with the following imaging parameter: random 2D stack-of-stars k-space sampling, TR/TE = 3/1.6 ms, flip angle = 7 degrees, image size = 256×256, resolution = 1.9×1.9×6 mm3. In total 10 k-space lines were acquired in every frame, including 1 navigator and 2 training lines, resulting in a temporal resolution of 30 ms per frame.In our current implementation, the neighborhoods were chosen based on the respiratory motion profiles, i.e. frames within the same respiratory phase were grouped in the same neighborhood. The respiratory phases were determined by tracking the position of the liver (Fig. 1 a). Figure 1 (b) shows that images in each neighborhood can be represented by a lower dimensional subspace compared to a global model. Figure 2 illustrates how the proposed model describes the local coordinates given by applying an affine transform $$${L}_c^{-1}$$$ to the global coordinates $$$T$$$ at each neighborhood.
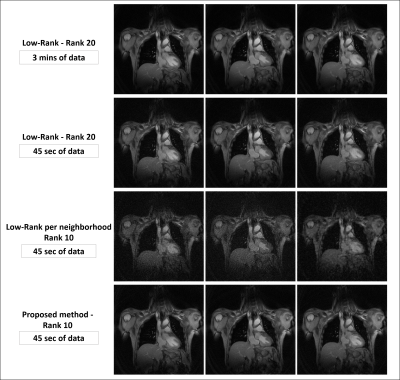
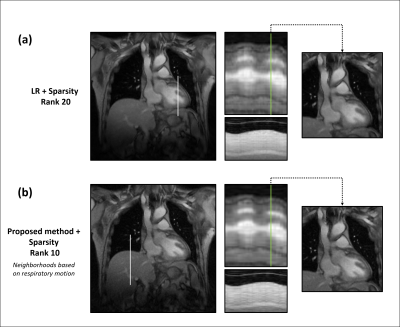
Overall, the proposed method successfully reconstructs 2D highly undersampled data with a rank twice as low as the LR method (10 vs 20), as much cardiac and respiratory features, and less noise without any sparsity constraint (Fig. 3 and 4). Note that the local LR does not yield a good reconstruction as the local coordinates are determined independently, unlike the proposed method (Fig. 3). A sparsity penalty term has then been added and tuned to decrease the noise yet keep as much motion detail as possible. There, the proposed method still outperforms conventional LR with images similarly smoothed but better-defined cardiac motion (Fig. 5).
Conclusion
We present a new approach to manifold learning-based image reconstruction for dynamic MR. The proposed method learns the geometries of the manifold locally and reconstructs images globally by aligning the subspaces in each neighborhood.Acknowledgements
This work was supported in part by NIH grants P41 EB022544, R01CA165221, and R01HL137230.
This work was partly done while I. Bloch was with LTCI, Télécom Paris, Institut Polytechnique de Paris, France.
References
1. Shepard, . R N, Kumar, ; v, Grama, A., Gupta, A. & Karypis, G. Nonlinear Dimensionality Reduction by Locally Linear Embedding. P. Y. Simard, Y. LeCun, J. Denker, Adv. Neural Info. Proc. Syst vol. 1 http://science.sciencemag.org/ (1994).
2. Tenenbaum, J. B., de Silva, V. & Langford, J. C. A global geometric framework for nonlinear dimensionality reduction. Science 290, 2319–2323 (2000).
3. Belkin, M. & Niyogi, P. Laplacian eigenmaps for dimensionality reduction and data representation. Neural Computation 15, (2003).
4. Ham, J., Lee, D. D., Mika, S. & Schölkopf, B. A kernel view of the dimensionality reduction of manifolds. in Proceedings, Twenty-First International Conference on Machine Learning, ICML 2004 369–376 (2004). doi:10.1145/1015330.1015417.
5. Nakarmi, U., Wang, Y., Lyu, J., Liang, D. & Ying, L. A Kernel-Based Low-Rank (KLR) Model for Low-Dimensional Manifold Recovery in Highly Accelerated Dynamic MRI. IEEE Transactions on Medical Imaging 36, 2297–2307 (2017).
6. Poddar, S. & Jacob, M. Dynamic MRI Using SmooThness Regularization on Manifolds (SToRM). IEEE Transactions on Medical Imaging 35, 1106–1115 (2016).
7. Zhang, Z. & Zha, H. Principal manifolds and nonlinear dimensionality reduction via tangent space alignment. SIAM Journal on Scientific Computing 26, 313–338 (2005).
8. Zhao, B., Haldar, J. P., Christodoulou, A. G. & Liang, Z.-P. Image Reconstruction From Highly Undersampled (k,t)-Space Data With Joint Partial Separability and Sparsity Constraints. IEEE transactions on medical imaging 31, 1809–1820 (2012). 9
9. He, J. et al. Accelerated High-Dimensional MR Imaging with Sparse Sampling Using Low-Rank Tensors. IEEE Transactions on Medical Imaging 35, 2119–2129 (2016).
10. Boyd, S., Parikh, N., Chu, E., Peleato, B. & Eckstein, J. Distributed optimization and statistical learning via the alternating direction method of multipliers. Foundations and Trends in Machine Learning vol. 3 1–122 (2010).
Figures
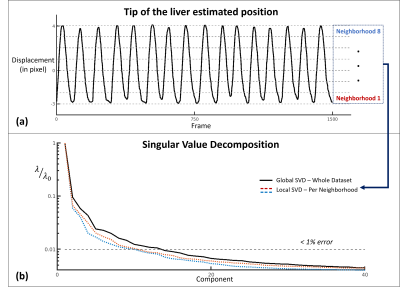
Figure 1: (a) Position of the liver throughout the acquisition. Estimated using an erf fitting on the edge of the liver using the reference LR images (rank 20) with 3 mins of data. 8 neighborhoods have been chosen based on the position of the liver.
(b) Singular value decomposition (SVD) of the concatenated training lines for both coils. The dotted lines show the decay of the singular values of the local Casorati matrices formed by the images within 2 representative neighborhoods. The solid line shows a slower decay of the singular values of the global Casorati matrix formed by all the images.