0067
Fast Calibrationless Image-space Reconstruction by Structured Low-rank Tensor Estimation of Coil Sensitivity and Spatial Support1Laboratory of Biomedical Imaging and Signal Processing, The University of Hong Kong, Hong Kong SAR, China, 2Department of Electrical and Electronic Engineering, The University of Hong Kong, Hong Kong SAR, China, 3Department of Electrical and Electronic Engineering, Southern University of Science and Technology, Shenzhen, China, 4College of Health Science and Environmental Engineering, Shenzhen Technology University, Shenzhen, China
Synopsis
In conventional parallel imaging, coil sensitivity information can be obtained from calibration data for reconstruction that inevitably prolongs MRI scan. In recent years, structured low-rank matrix completion methods implicitly exploit coil sensitivity that enables calibrationless k-space estimation while prohibitively increases the computational burden. This study presents a fast and calibrationless image-space alternative for reconstruction that derives high-quality coil sensitivity and spatial support maps by structured low-rank tensor estimation. The proposed approach was evaluated with multi-channel multi-contrast brain datasets. It achieves a high convergence rate with significantly reduced reconstruction time, making the calibrationless reconstruction approach more efficient in clinical practice.
Introduction
Parallel imaging has been applied routinely, which can be categorized as using the explicit knowledge of coil sensitivity (e.g., SENSE1) or exploiting the corresponding k-space relation (e.g., GRAPPA2) from either the calibration scan or autocalibrating signals. Calibrationless low-rank techniques3-5 enable simultaneous autocalibration and k-space reconstruction while prohibitively increase the computational burden, especially for clinical multi-modality MRI. In this study, we propose a fast and calibrationless image-space alternative for reconstruction that can efficiently derive high-quality coil sensitivity and spatial support6,7 maps by the low-rank method. This developed approach significantly reduces the computation time for reconstructing multi-channel multi-contrast MR datasets and yields comparable image quality to corresponding calibrationless low-rank reconstruction8-10.Theory and Methods
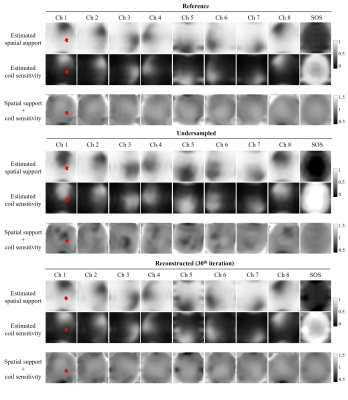
Structured Low-rank Tensor Estimation for Coil Sensitivity and Spatial SupportCalibrationless low-rank reconstruction can be typically described as the subspace approach that characterizes linear relations of MR k-space data by forming a structured low-rank matrix. In theory, the signal and null subspace of such structured matrix are spanned by coil sensitivity (presented as eigenvectors11) and spatial support12,13. To efficiently estimate shared coil sensitivity and spatial support in this study, multi-contrast k-space data has been structured into a low-rank tensor, as shown in Figure 1. Subsequent higher-order singular value decomposition serves to identify both the signal- and null- subspace bases. Note that the proposed method transforms all bases to image space rather than directly approximating k-space data in conventional low-rank reconstruction. As each subspace base characterizes part of coil sensitivity and spatial support information, the summation of bases would estimate coil sensitivity and spatial support maps without losing the phase information.
Image-space Reconstruction
With estimated coil sensitivity maps, the standard SENSE reconstruction can be performed to provides a regularized least-squares solution. In the proposed method, multi-channel spatial support maps derived from null-subspace bases are also incorporated for more accurate SENSE reconstruction with the observation that estimated coil sensitivity and spatial support are nearly orthogonal complements with each other (coil sensitivity + spatial support = 1 for every pixel). While coil sensitivity and spatial support maps derived from calibrationless low-rank tensor estimation may contain errors due to undersampling, the proposed reconstruction is performed as the iterative estimation of coil sensitivity and MR images with a high convergency rate. As a comparison, corresponding calibrationless low-rank reconstruction (MC-HTC)9,10 has been performed that iteratively approximates the low-rank tensor and enforces data consistency.
Data Preparation
Fully sampled 8-channel brain datasets of four typical MRI contrasts were acquired on a 3T scanner (Philips Healthcare, Best, Netherland) with identical locations (matrix size 200 × 200). For T1-weighted (T1W) acquisition, 2D fast field echo (FFE) was used. For T2-weighted (T2W), fluid-attenuated inversion recovery (FLAIR), and T1-weighted inversion recovery (T1W-IR) acquisitions, 2D fast spin echo (FSE) was used.
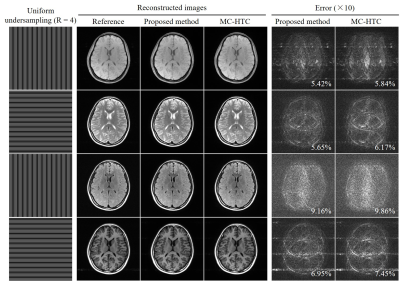
For evaluation, multi-contrast k-space data were retrospectively undersampled using uniform undersampling patterns (R = 4) with phase-encoding directions orthogonally alternated among different contrasts to enhance sampling incoherency in low-rank estimation.
Results
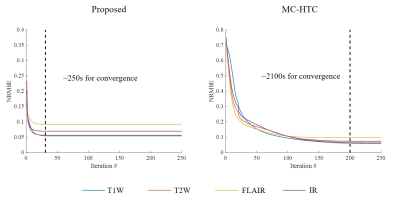
As shown in Figure 2, coil sensitivity and spatial support maps estimated from fully sampled reference data are nearly orthogonal complements for each channel and sum-of-square (SOS) combined images within the brain region. In contrast, coil sensitivity and spatial support maps have estimation errors due to undersampling but can be efficiently corrected after the proposed iterative image-space reconstruction. The proposed method exhibited a rapid convergency rate (Figure 3) and required only 250 seconds (using a personal desktop with 4-core i5-6500 and 16GB RAM) for jointly reconstructing 8-channel 4-contrast datasets (1 minute per contrast), whereas the corresponding k-space low-rank reconstruction was at least 8 times slower. This fast approach provided very similar reconstruction performance without compromising image quality (Figure 4).Discussion and Conclusions
This study presents a fast and calibrationless image-space reconstruction alternative to k-space reconstruction for multi-contrast MRI. This approach estimates both coil sensitivity and spatial support maps by low-rank tensor estimation, which can be considered as converting calibrationless low-rank reconstruction into efficient iterative SENSE reconstruction. Although this approach was demonstrated by jointly reconstructing multi-contrast images using low-rank tensor estimation in this study, it can also generalize to other structured low-rank methods based on subspace analysis, making the existing calibrationless reconstruction approach more efficient in clinical practice. Note that this approach exhibits rapid convergency rate and thus may yield a magnitude order of acceleration in reconstruction time by using a larger (even 3D) kernel for constructing the low-rank matrix/tensor.Several methods have also considered exploiting k-space data relation for estimating either coil sensitivity (e.g., ESPIRiT11) or spatial support (e.g., PRUNO12 and AC-LORAKS14), but none of them utilizing both coil sensitivity and spatial support with complementary information. More importantly, all these methods require calibration data that may suffer from inaccuracy caused by motion, causing artifacts in reconstruction. Note that the proposed method can provide high-quality coil sensitivity maps with coil sensitivity information only around the brain region. This can be considered as simultaneously achieving the estimation and masking of coil sensitivity maps that can suppress the propagation of noise in the background region during reconstruction.
Acknowledgements
This study was supported by Hong Kong Research Grant Council (R7003-19, C7048-16G, HKU17112120, HKU17103819 and HKU17104020), Guangdong Key Technologies for Treatment of Brain Disorders (2018B030332001), and Guangdong Key Technologies for Alzheimer’s Disease Diagnosis and Treatment (2018B030336001).References
[1] Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. SENSE: Sensitivity encoding for fast MRI. Magn Reson Med 1999;42(5):952-962.
[2] Griswold MA, Jakob PM, Heidemann RM et al. Generalized autocalibrating partially parallel acquisitions (GRAPPA). Magn Reson Med 2002;47(6):1202-1210.
[3] Shin PJ, Larson PEZ, Ohliger MA et al. Calibrationless parallel imaging reconstruction based on structured low-rank matrix completion. Magn Reson Med 2014;72(4):959-970.
[4] Haldar JP, Zhuo J. P-LORAKS: Low-rank modeling of local k-space neighborhoods with parallel imaging data. Magn Reson Med 2016;75(4):1499-1514.
[5] Lee D, Jin KH, Kim EY, Park SH, Ye JC. Acceleration of MR parameter mapping using annihilating filter-based low rank hankel matrix (ALOHA). Magn Reson Med 2016;76(6):1848-1864.
[6] Plevritis SK, Macovski A. Spectral extrapolation of spatially bounded images [MRI application]. IEEE Trans Med Imaging 1995;14(3):487-497.
[7] Haldar JP. Low-Rank Modeling of Local k-Space Neighborhoods (LORAKS) for Constrained MRI. IEEE Trans Med Imaging 2014;33(3):668-681.
[8] Liu Y, Cao J, Lyu M, Wu E. Calibration-less parallel imaging reconstruction using hankel tensor completion (HTC). In: Proceedings of the 25th Annual Meeting of ISMRM, Honolulu, HI, USA, 2017, p 445.
[9] Yi Z, Liu Y, Chen F, Wu E. Joint Calibrationless Reconstruction of Highly Undersampled Multi-contrast MR Datasets Using A Novel Low-Rank Completion Approach. In: Proceedings of the 27th Annual Meeting of ISMRM, Montreal, QC, Canada, 2019, p 4746.
[10] Liu Y, Yi Z, Zhao Y et al. Calibrationless parallel imaging reconstruction for multislice MR data using low-rank tensor completion. Magn Reson Med 2021;85(2):897-911.
[11] Uecker M, Lai P, Murphy MJ et al. ESPIRiT-an eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA. Magn Reson Med 2014;71(3):990-1001.
[12] Zhang J, Liu C, Moseley ME. Parallel reconstruction using null operations. Magn Reson Med 2011;66(5):1241-1253.
[13] Haldar JP, Setsompop K. Linear Predictability in Magnetic Resonance Imaging Reconstruction: Leveraging Shift-Invariant Fourier Structure for Faster and Better Imaging. IEEE Signal Processing Magazine 2020;37(1):69-82.
[14] Lobos RA, Javed A, Nayak KS, Hoge WS, Haldar JP. ROBUST AUTOCALIBRATED LORAKS FOR EPI GHOST CORRECTION. Proceedings IEEE International Symposium on Biomedical Imaging 2018;2018:663-666.
Figures