0064

Region-Optimized Virtual (ROVir) Coils: Application of Sensor-Domain Beamforming for Localizing and/or Suppressing Spatial Regions

Daeun Kim¹, Stephen F. Cauley², Krishna S. Nayak¹, Richard M. Leahy¹, and Justin P. Haldar¹
¹Electrical and Computer Engineering, University of Southern California, Los Angeles, CA, United States, ²Radiology, A. A. Martinos Center for Biomedical Imaging, Massachusetts General Hospital, Charlestown, MA, United States

Synopsis

MRI acquisitions often incidentally excite spatial regions that are not interesting for the application. This unnecessary magnetization can lead to artifacts and/or prolonged acquisitions. We propose a novel virtual-coil approach, called region-optimized virtual (ROVir) coils, that can localize signal from an ROI and/or suppress signal from unwanted spatial regions while also providing coil compression. This is achieved using optimal beamforming principles (without requiring modification of pulse sequences or imaging hardware), and can be applied directly to k-space data, which enables simplified image reconstruction. We illustrate ROVir with reduced-FOV imaging, demonstrating capabilities to suppress aliasing artifacts from outside the nominal FOV.

Introduction

Typical MRI experiments often incidentally excite spatial regions that are not interesting for the application. Excitation of uninteresting regions can complicate the design of efficient imaging methods, leading to artifacts and/or acquisitions that are longer than necessary.

We propose a novel approach to localizing the signal from a region-of-interest (ROI) and/or suppressing the signal from uninteresting spatial regions. While there are many hardware- and sequence-based approaches that address this problem, the proposed approach instead uses the beamforming capabilities^1,2 of a phased array of receiver coils to enable the suppression of unwanted signals without modifying the acquisition hardware or pulse sequence. The proposed approach linearly mixes the signal from the original receiver coils to form a set of coil-compressed region-optimized virtual (ROVir) coils that are optimal in the sense that they maximize a signal-to-interference ratio (SIR) metric. Importantly, unlike existing beamforming approaches that use different coil combinations at different spatial locations and can only be used for post-processing of already-reconstructed images^3-9, ROVir uses a form of spatially-invariant beamforming (“sensor-domain beamforming”) that can be applied directly to raw k-space data prior to image reconstruction. This enables simplified image reconstruction. In addition, unlike existing coil compression approaches that only attempt to maximize signal^10-11, ROVir is also capable of actively suppressing unwanted signal. Finally, unlike recent similar sensor-domain approaches¹², ROVir possesses mathematical optimality.

Theory

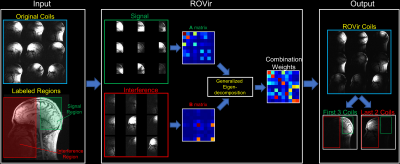
We consider the standard virtual coil paradigm, in which original multi-channel k-space data, $$$d_l(\mathbf{k})$$$, for $$$l=1,\dots,N_c$$$ from $$$N_c$$$ original coils are linearly transformed into data $$$v_j(\mathbf{k})$$$ from a smaller number of $$$N_v$$$ virtual coils according to $$$v_j(\mathbf{k})=\sum_{l=1}^{N_c} w_{lj} d_l(\mathbf{k})$$$ for $$$j=1,\dots,N_v$$$. To achieve both coil-compression and signal localization/suppression, ROVir chooses the $$$\left\{ w_{lj} \right\}$$$ linear coil-combination coefficients to maximize an SIR metric, which is defined by the ratio between the signal energy from the spatial region of interest and the interference energy from unwanted spatial regions. After some manipulation, it can be shown that this is equivalent to: $$ \text{SIR}(\mathbf{w}_j) \triangleq \frac{\mathbf{w}_j^H \mathbf{A} \mathbf{w}_j}{\mathbf{w}_j^H \mathbf{B} \mathbf{w}_j},$$ where $$$\mathbf{w}_j \in \mathbb{C}^{N_c}$$$ is the vector of weighting coefficients $$$ \left \{ w_{lj} \right \}$$$. The matrices $$$\mathbf{A} \in \mathbb{C}^{N_c \times N_c}$$$ and $$$\mathbf{B} \in \mathbb{C}^{N_c \times N_c}$$$ are constructed as inter-coil correlation matrices corresponding to the spatial region of interest $$$\Omega$$$ and the unwanted spatial regions $$$\Gamma$$$, respectively, defined by: $$\mathbf{A} \triangleq \int_\Omega \mathbf{g}(\mathbf{x}) \mathbf{g} (\mathbf{x})^{H} d\mathbf{x}, ~~\text{and}~~\mathbf{B} \triangleq \int_\Gamma \mathbf{g}(\mathbf{x}) \mathbf{g} (\mathbf{x})^{H} d\mathbf{x},$$ with $$$ \mathbf{g} (\mathbf{x}) \in \mathbb{C}^{1\times N_c} \triangleq \left[ g_1(\mathbf{x}),\dots, g_{N_c}(\mathbf{x}) \right]$$$ where $$$ g_l(\mathbf{x})$$$ is the sensitivity weighted image for the $$$ l $$$th coil.

The optimal weight vectors can be found by a simple generalized eigenvalue decomposition for $$$\mathbf{A}$$$ and $$$\mathbf{B}$$$^1-2. The generalized eigenvectors with the largest eigenvalues will have maximal SIR, and SIR-optimal ROVir coils are obtained by keeping the top- eigenvectors. In practice, the $$$\mathbf{A}$$$ and $$$\mathbf{B}$$$ matrices can be computed using the same kind of prescan/calibration data that is already used for parallel imaging. Once the optimal ROVir weights are calculated, they can then be applied directly to raw k-space data of subsequent scans. Figure 1 provides a representative illustration of ROVir.

Methods

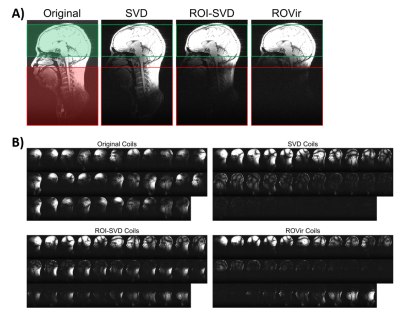
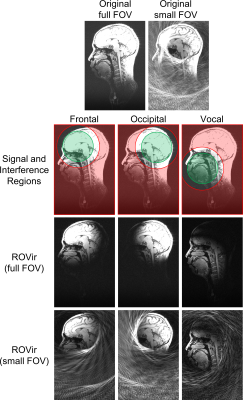
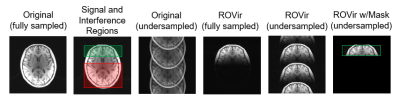
Brain imaging example: We applied ROVir to in vivo T1-weighted brain imaging data acquired with a 32-channel array, and performed comparisons against conventional SVD and ROI-focused SVD (ROI-SVD) coil-compression approaches^10-11. We considered a scenario where we are interested in the signal from the brain, but not in the signal from other parts of the head, neck, or torso.

Application to reduced-FOV: One potential application of ROVir could be to reduce the size of the image support, enabling small FOV imaging. As examples, we applied ROVir to reduced-FOV head imaging. Using 32-channel brain data, we retrospectively simulated a spiral k-space trajectory designed for a small FOV, as well as a Cartesian k-space trajectory designed for a small FOV. Reconstructions were performed with standard gridding/Fourier transform reconstruction, with and without ROVir.

Results

Figure 2 shows a comparison of ROVir against SVD and ROI-SVD coil compression methods. The results demonstrate that ROVir can substantially suppress the interference, compacting energy from the ROI into the first virtual coils, while also compacting energy from the unwanted spatial region into the last virtual coils. Keeping only the first few virtual coils successfully suppresses unwanted spatial regions.

Results for non-cartesian reduced-FOV imaging are shown in Fig. 3 for different ROIs, demonstrating that ROVir enables aliasing-free depictions of each ROI by suppressing the interference from unwanted regions. Fig. 4 demonstrates that beam-steering can be used to allow ROVir to focus on arbitrary ROIs within the FOV. Figure 5 shows similar reduced-FOV results in the context of Cartesian acquisition.

Conclusion

This work proposed ROVir, a simple beamforming framework that can be used to localize an ROI and suppress signal from unwanted spatial regions. ROVir is compatible with and complementary to existing signal localization/suppression methods. While we only showed examples involving simple image reconstruction methods, ROVir can be applied directly to raw and potentially undersampled k-space data, and can potentially be used in combination with arbitrary image reconstruction methods. We believe that this approach is potentially useful for a wide range of different MRI applications that would benefit from improved signal localization/suppression.

Acknowledgements

This work was supported by research grants NIH R01-MH116173, NIH R01-NS074980, and NIH R01-NS089212 and R33-CA225400.

References

1. Van Veen BD, Buckley KM. Beamforming: A versatile approach to spatial filtering. IEEE ASSP Mag 1988;5:4-24.

2. Monzingo RA, Haupt RL, Miller TW. Introduction to Adaptive Arrays. Raleigh: SciTech Publishing. 2011.

3. Roemer PB, Edelstein WA, Hayes CE, Souza SP, Mueller OM. The NMR phased array. Magn Reson Med 1990;16:192-225.

4. Walsh DO, Gmitro AF, Marcellin MW. Adaptive reconstruction of phased array MR imagery. Magn Reson Med 2000;43:682-690.

5. Kellman P, McVeigh ER. Ghost artifact cancellation using phased array processing. Magn Reson Med 2001;46:335-343.

6. H Eggers PB P Boernert. Real-time partial parallel spiral imaging with localized sensitivities. In: Proc. Int Soc Magn Reson Med 2001; p. 1772.

7. Lin FH, Witzel T, Ze_ro TA, Belliveau JW. Linear constraint minimum variance beamformer functional magnetic resonance inverse imaging. NeuroImage 2008;43:297-311.

8. Ebbini E, DelaBarre L, Vaughan JT, Gopinath A. Digital beamforming in MRI. In:Proc. IEEE BenMAS. 2014.

9. Mandava S, Keerthivasan MB, Martin DR, Altbach MI, Bilgin A. Radial streak artifact reduction using phased array beamforming. Magn Reson Med 2019;81:3915-3923.

10. Buehrer M, Pruessmann KP, Boesiger P, Kozerke S. Array compression for MRI with large coil arrays. Magn Reson Med 2007;57:1131-1139.

11. Huang F, Vijayakumar S, Li Y, Hertel S, Duensing GR. A software channel compression technique for faster reconstruction with many channels. Magn Reson Imag 2008;26:133-141.

12. Cauley S, Polak D, Liu W, Bilgic B, Gagoski B, Grant PE, Conklin J, Kirsch J, Huang SY, Setsompop K, Wald LL. Geometric coil mixing (GCM) to dampen confounding signals in MRI reconstruction. In: Proc. Int. Soc. Magn. Reson. Med.. 2019; p. 449.

13. Jackson JI, Meyer CH, Nishimura DG, Macovski A. Selection of a convolution function for Fourier inversion using gridding. IEEE Trans Med Imag 1991;10:473-478.

14. Griswold MA, Jakob PM, Nittka M, Goldfarb JW, Haase A. Partially parallel imaging with localized sensitivities (PILS). Magn Reson Med 2000;44:602-609.

Figures

Figure 1. Illustration of ROVir. From an original set of coils, the ROVir approach forms region-specific inter-coil correlation matrices A (signal) and B (interference), which are used to compute coil combination weights that optimize the signal-to-interference ratio through a generalized eigendecomposition procedure. The ROVir coils that result from using these combination weights have excellent separation between the signal and interference regions, and are also highly-effective at compressing the high-dimensional coil array into a much smaller number of relevant coils.

Figure 2. Brain imaging example. A) Coil-combined images from (left) an original 32-channel dataset and (right) coil-compressed virtual coil arrays obtained using SVD, ROI-SVD, and ROVir, respectively. The ROI signal that was used in this case is marked in green, while the “interference" region is marked in red. B) The individual coil images corresponding to the different cases from A. For each set of virtual coils, the coils are shown in order from left to right and top to bottom.

Figure 3. Application of ROVir to reduce the size of the FOV in non-cartesian sagittal brain imaging, which enables highly-effective mitigation of aliasing artifacts when using a spiral k-space trajectory designed for a smaller FOV. The signal ROIs are marked in green, while the interference regions are marked in red. Reconstruction was based on simple gridding¹³.

Figure 4. Illustration of using beamforming to steer the sensitivity of the virtual array to different spatial positions. The video shows ROVir results obtained from sweeping a circular-shaped ROI (i.e., everything interior to the green circle) through the FOV for a 32-channel brain MRI dataset.

Figure 5. Application of ROVir to reduced-FOV Cartesian imaging. Undersampling k-space data by a factor of 3 (equivalent to using a small FOV) causes aliasing artifacts when using the original coils, while ROVir effectively suppresses unwanted signal, leading to alias-free images. The signal and interference regions are marked in green and red. Reconstruction was based on simple Fourier reconstruction. This approach to localization follows the same principles as PILS¹⁴, although can be achieved virtually in post-processing without requiring specially-designed PILS coils.

Proc. Intl. Soc. Mag. Reson. Med. 29 (2021)

0064