Introduction

DCE-MRI is widely used for detecting and characterizing tumors and other lesions. Typically, images are rapidly acquired in different contrast-enhancement phases. Golden-Angle Radial Sparse Parallel (GRASP) MRI^[1] is a recently proposed reconstruction technique which provides high spatial and temporal resolutions for DCE-MRI. L+S decomposition^[2] is another reconstruction scheme which subdivides image series into temporally correlated background L and dynamic varied sparse information S. It enables an efficient reconstruction using Iterative Soft Thresholding Algorithm (ISTA). Both GRASP and L+S decomposition employ the temporal Total Variation (TV) as the sparsity transform to eliminate the temporal variations. However, dynamic contrast signal induced by injecting the contrast agent gradually varies along the temporal dimension. The “averaging effect” from the temporal TV degrades the dynamic contrast of DCE-MRI. Temporal FFT is another sparsity constraint which explores the temporal sparsity through gradually eliminating frequency components with negligible magnitude. Since the intensity of DCE signal is assumed to be varying temporally at low frequency, these low frequency components can be reserved by temporal FFT to maintain the dynamic contrast. Here, we introduce both temporal FFT and temporal TV to L+S model, compressing the undersampling artefacts and maintaining the dynamic contrast simultaneously for improved DCE-MRI reconstruction.

Method

The proposed reconstruction scheme is mathematically formulated as: $$ argmin_{L,S}=\frac{1}{2}\left \| E(L+S)-d \right \|_{2}^{2}+\lambda_{L}\left \| L \right \|_{*}+\lambda_{T}\left \| TS \right \|_{1}+\lambda_{F}\left \| FS \right \|_{1} \qquad \qquad [1]$$ where $$$ E $$$ is the multi-coil encoding operator and $$$ d $$$ is the acquired data. $$$ T $$$ is the temporal TV sparsity transform while $$$ F $$$ is the temporal FFT based sparsity transform, and parameters $$$ \lambda_{L} $$$ , $$$ \lambda_{T} $$$ and $$$ \lambda_{F} $$$ are trade off data consistency versus complexity of solution given by the nuclear norm $$$ \left \| \cdot \right \|_{*} $$$ and $$$ L_{1} $$$ norm $$$ \left \| \cdot \right \|_{1} $$$.


Two golden angle radial sampled datasets including a simulated phantom dataset and a free breathing liver DCE-MRI dataset were adopted to evaluate the performance of the proposed method. A shepp-logan computer model with 384*384 voxels was created, and the simulation was performed by solving Bloch equations. Eight different sensitivity field maps were integrated into the simulation, forming multiple virtual channels. Signal intensity of certain areas of the shepp-logan phantom were varied with the designed dynamic contrast model as used in ^[1]. A total of 588 spokes with 384 readout points in each spoke were acquired. A group of fully sampled reference images were generated as the benchmark. A free breathing liver DCE-MRI dataset offered by Li et al ^[1] was adopted. The corresponding parameters for the liver dataset: TR/TE=3.52/1.41ms, 8 channels, 588 spokes with 384 readout points each. Both two datasets were subdivided into 21 frames with the temporal resolution of 28 spokes/frame. The corresponding acceleration factor is 21.5. These two datasets were reconstructed and compared by using NUFFT, standard GRASP, L+S decomposition and our proposed method. FCSA ^[3-5] was employed to solve the reconstruction scheme with multiple constraints in the proposed model. All the reconstructions were repeated 10 times. The Euclidean distance between the reconstructed DCE curves and the reference curve was calculated to evaluate the performance of capturing the dynamic signal changes for each method. The average reconstruction time, the peak DCE signal and the average DCE signal were calculated and compared for both datasets using all methods. All the reconstructions were performed using MATLAB 2019b (MathWorks, Natick, MA) on an Intel Core i7-4790 PC with a 3.6 GHz processor.

Results & Discussion

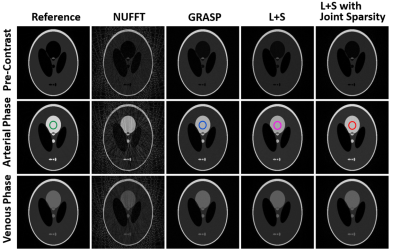
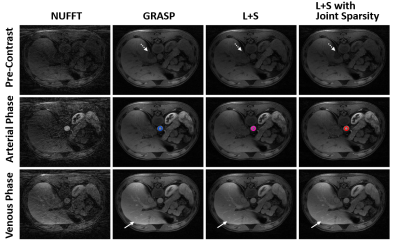
Figure 1 and Figure 2 show a comparison of GRASP, standard L+S and L+S with joint sparsity in reconstructing the simulated phantom dataset and free breathing liver dataset respectively. For liver dataset, two L+S based techniques present better background structure of liver. Better dynamic contrast of tissues (labelled by solid arrows) was observed in GRASP and the proposed method. Blurring was observed in standard L+S reconstruction (labelled by dashed arrows) due to the degradation of dynamic contrast. Figure 3 and Figure 4 demonstrate the average reconstruction time and corresponding dynamic performance of the three schemes in two datasets. Our proposed method and standard L+S achieved similar reconstruction efficiency. The peak of dynamic signal was degraded by 12.7%, 19% and 20.7% for our proposed method, GRASP and standard L+S method compared to the reference. Using the reference dynamic curve as the benchmark, the Euclidean distance of our proposed method is 0.0157 which is much smaller other two schemes, suggesting that our method can capture the dynamic varying arterial signals much better as shown in Figure 4a. In Figure 4b, the peak dynamic signal in liver dataset in the proposed method demonstrated an increase in peak DCE signal by 24.8% and 33% than that of GRASP and standard L+S method respectively.

Conclusion

A low rank with joint sparsity framework is proposed and evaluated for improved DCE-MRI reconstruction. Our proposed L+S based method achieved around 4 times faster reconstruction speed than GRASP method. The computation cost from additional sparsity constraint is negligible with the support of FCSA. Clear improvement of dynamic contrast was achieved by utilizing joint sparsity constraints in the proposed method.

Acknowledgements

National Key R&D Program of China: 2019YFC0118700