0049

Free-Breathing Motion-Informed Quantitative 3D Myocardial Perfusion Imaging

Tobias Hoh¹, Valery Vishnevskiy¹, Maximilian Fuetterer¹, and Sebastian Kozerke¹
¹Institute for Biomedical Engineering (IBT), University and ETH Zurich, Zurich, Switzerland

Synopsis

Three-dimensional perfusion CMR requires acceleration methods to enable whole-heart coverage in short acquisition windows, which often rely on data correlation among adjacent time-frames. However, in free-breathing examinations, respiratory motion leads to inconsistencies in the shared data and compromises image quality. In this work, non-rigid organ motion is incorporated into a patch-based locally low-rank reconstruction algorithm as a transformation displacement field for each time frame. This motion-informed locally low-rank reconstruction, combined with Cartesian pseudo-spiral k-t undersampling, is proposed as a dual-sequence acquisition framework to enable quantitative free-breathing whole-heart perfusion CMR. Feasibility is demonstrated in simulations, and volunteers in rest and stress.

Introduction

Three-dimensional first-pass myocardial perfusion CMR requires acceleration methods such as k-t undersampling or compressed sensing to enable whole-heart coverage in a limited acquisition window¹. While data correlations in the k-t domain have been successfully exploited², data inconsistencies during free-breathing can significantly compromise image quality. As profile binning approaches are not suited for non-continuous acquisitions^3-6, data-driven respiratory motion compensation has to be incorporated into the iterative image reconstruction^7,8.
In the present work, a Cartesian pseudo-spiral k-t undersampling scheme with respiratory motion-informed locally low-rank reconstruction (MI-LLR) is proposed. Utilizing data correlation using patch-based decomposition of the multi-dimensional data frames [9] and by incorporating a transformation displacement field for each time frame, MI-LLR is able to correct for non-rigid organ motion enabling robust free-breathing whole-heart myocardial perfusion CMR. The acquisition and reconstruction framework was implemented using a dual sequence design¹⁰. Simulations were performed to assess accuracy and in vivo feasibility is demonstrated under rest and stress.

Methods

Data acquisition
A 2D/3D dual-sequence design was implemented¹¹. The proposed 3D pseudo-spiral Cartesian k-t sampling pattern, which acquires 120 samples per time frame (undersampling factor 10x) from a weighted density distribution is illustrated in Figure 1a.
Imaging parameters were:$$$\;TR/TE\;=\;2.0/1.0\;ms$$$, spatial resolution:$$$\;2.5x2.5x10\;mm^3$$$,$$$\;FA:15°$$$, acquisition window:$$$\;240\;ms$$$, and a saturation delay:$$$\;135\;ms$$$. For interleaved imaging of the arterial input function (AIF), a center-out Cartesian sampling with 25 profiles was used: spatial resolution:$$$\;12.0\;x\;12.0\;mm^2$$$, slice thickness:$$$\;15\;mm,\;FA:15°$$$, acquisition window:$$$\;56\;ms$$$, saturation delay:$$$\;25\;ms$$$.
All images were acquired on a 1.5 T Philips Achieva MR system (Philips Healthcare) using a 5-element cardiac receive coil array.
Three healthy volunteers were examined upon written informed consent. Two consecutive experiments with contrast agent (Gadovist, Bayer Schering Pharma) bolus injections of 0.075 mmol/kg b.w. at 4 ml/s were performed 15 min apart to compare imaging at rest and during adenosine-induced stress.

Reconstruction
Imaging data$$$\;\bf{I}\;$$$was reconstructed according to:
$$\min_{\bf{I}}||\bf{\Omega}\mathcal{\bf{F}}\bf{S}\bf{I}-\bf{d}||_2^2+\lambda\sum_{\it{b}\in\it{U}}||\bf{P}_{\it{b}}\bf{I}||_*\;,$$
with the undersampling operator$$$\;\bf{\Omega}$$$, Fourier transform$$$\;\bf{F}$$$, coil sensitivities $$$\;\bf{S}$$$, k-space data$$$\;\bf{d}\;$$$and regularization weights$$$\;\lambda$$$. The patchifying operator$$$\;\bf{P}_{\it{b}}\;$$$refers to the b-th patch, where$$$\;\it{U}\;$$$is a set of patch indices. The asterisk indicates the nuclear norm. At each iteration, patches are selected randomly to avoid blocking artefacts.
Motion-related displacement fields$$$\;\bf{D}_{\it{t}}\;$$$were inverted using linear interpolation$$$\;\bf{D}_{\it{t}}^{-1}\approx\mathcal{\bf{Q}}_{\it{t}}$$$. Hence, linear operators$$$\;\mathcal{\bf{Q}}_{\it{t}}\;$$$were used to map a fixed reference frame to the target configuration t, which allowed to regularize images in the motion-compensated configuration:
$$\min_{\bf{I}}||\bf{\Omega}\mathcal{\bf{F}}\bf{S}[\mathcal{\bf{Q_1}}\bf{i}_1,...,\mathcal{\bf{Q_T}}\bf{i}_T]-\bf{d}||_2^2+\lambda\sum_{\it{b}\in\it{U}}||\bf{P}_{\it{b}}\bf{I}||_*\;,$$
where$$$\;\bf{I}=[\bf{i}_1,...,\bf{i}_T]$$$. Note that this optimization problem is convex and allows to use a proximal gradient descent (PGD) method¹², which was implemented in Matlab (The MathWorks Inc., Natick, MA) on GPUs. Sensitivity maps for coil calibration were estimated from reference scans using the ESPIRiT method¹³. Displacement fields$$$\;\bf{D}_{\it{t}}\;$$$were estimated with the pTVreg library¹⁴.

The entire framework is schematically outlined in Figure 1b-d. In a first run, images are reconstructed using LLR (Equation 1), a patch size of nx=ny=nz=12, with low regularization to capture spatiotemporal image variations$$$\;(\lambda_{low}\;=\;0.05)$$$. Thereafter, the MI-LLR problem is solved with the smallest regularization that suppresses background signal variation to 0.05 % of the maximum image intensity.

Postprocessing
Post-processing and perfusion quantification were conducted in MATLAB.The myocardium was segmented into six circumferential sectors across ten slices. Absolute perfusion quantification of MBF was performed using Fermi model deconvolution^11,15.

Simulation studies
Numerical simulations based on the MRXCAT simulation framework¹⁶ were performed to validate MI-LLR. A ground truth (GT) phantom with 1.25x1.25x5 mm³ was sampled according to parameters applied in-vivo and using the signal model¹⁵, including partial voluming and motion during readout effects.

Results

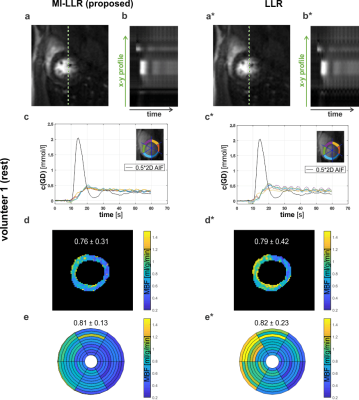
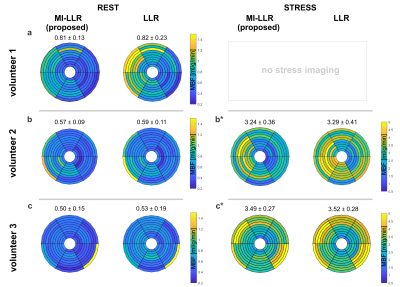
Simulation results indicate improved accuracy of global MBF quantification and reduced intra-subject variability for MI-LLR over LLR (Figure 2). Elevated signal time curves, as well as myocardial perfusion maps, show signal shading from the blood pools in the septal region of the myocardium.
For in-vivo case at rest, Figure 3, MI-LLR shows improved image quality while standard LLR shows blurring and residual motion in image and concentration time curves. MBF variation was reduced using MI-LLR (STD = ±0.13 vs. ±0.23 ml/g/min), where midventricular, infero- and anteroseptal regional means are more homogeneous.
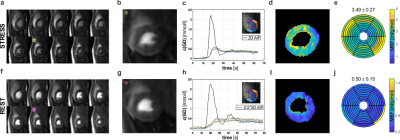
Exemplary quantification results and image quality are shown in Figure 4. Image series, concentration time curves and MBF maps demonstrate fidelity and spatial homogeneity. Under stress, regional deviations at the basal level are associated with inflow artifacts.
MBF quantification results for all subjects are summarized in Figure 5. For RC-LLR / standard LLR reconstruction, average MBF under rest was 0.63±0.08 ml/g/min / 0.65±0.18 ml/g/min, whereas under stress 3.37±0.32 ml/g/min / 3.41±0.35 ml/g/min, respectively. A reduction in myocardial variability was found in all cases.

Discussion

We presented an accelerated Cartesian pseudo-spiral k-t acquisition for 3D perfusion CMR and proposed an effective method for motion-compensated reconstruction: MI-LLR.
Feasibility was demonstrated in simulations and volunteer examinations at rest and stress. The proposed MI-LLR showed quantitative improvement compared to the standard LLR reconstruction for the clinically desired free-breathing and thus enables whole-heart perfusion assessment. MI-LLR reduces signal overestimation in the challenging septal region, contaminated by high contrast signal from the blood pool. The derived MBF values lie within reported ranges for established quantitative 2D perfusion CMR methods¹⁷.
Next steps entail further hyperparameter tuning and validation, as well as improved sensitivity correction, to ensure physiologically correct mean values. Feasibility for higher acceleration factors, to reduce intra-shot contractile motion, will be investigated.

Acknowledgements

No acknowledgement found.

References

1. Fair MJ, Gatehouse PD, DiBella EVR, Firmin DN. A review of 3D first-pass, whole-heart, myocardial perfusion cardiovascular magnetic resonance. J. Cardiovasc. Magn. Reson. 2015;17:1–25
2. Manka R, Gebker R, Wissmann L, et al. Multicenter evaluation of dynamic three-dimensional whole-heart myocardial perfusion imaging for the detection of coronary artery disease defined by fractional flow reserve. J. Cardiovasc. Magn. Reson. 2013;15:190–191
3. Likhite D, Adluru G, Hu N, McGann C, Dibella E. Quantification of myocardial perfusion with self-gated cardiovascular magnetic resonance. J. Cardiovasc. Magn. Reson. 2015;17:1–15
4. Adluru G, McGann C, Speier P, Kholmovski EG, Shaaban A, Dibella EVR. Acquisition and reconstruction of undersampled radial data for myocardial perfusion magnetic resonance imaging. J. Magn. Reson. Imaging 2009;29:466–473
5. Feng L, Axel L, Chandarana H, Block KT, Sodickson DK, Otazo R. XD-GRASP: Golden-angle radial MRI with reconstruction of extra motion-state dimensions using compressed sensing. Magn. Reson. Med. 2016;75:775–788
6. Tian Y, Mendes J, Wilson B, et al. Whole-heart, ungated, free-breathing, cardiac-phase-resolved myocardial perfusion MRI by using Continuous Radial Interleaved simultaneous Multi-slice acquisitions at sPoiled steady-state (CRIMP). Magn. Reson. Med. 2020;84:3071–3087
7. Schmidt JFM, Wissmann L, Manka R, Kozerke S. Iterative k-t principal component analysis with nonrigid motion correction for dynamic three-dimensional cardiac perfusion imaging. Magn. Reson. Med. 2014;72:68–79
8. Akçakaya M, Basha TA, Pflugi S, et al. Localized spatio-temporal constraints for accelerated CMR perfusion. Magn. Reson. Med. 2014;72:629–639
9. Zhang T, Pauly JM, Levesque IR. Accelerating parameter mapping with a locally low rank constraint. Magn. Reson. Med. 2015;73:655–661
10. Gatehouse PD, Elkington AG, Ablitt NA, Yang G-Z, Pennell DJ, Firmin DN. Accurate assessment of the arterial input function during high-dose myocardial perfusion cardiovascular magnetic resonance. J. Magn. Reson. Imaging 2004;20:39–45
11. Wissmann L, Niemann M, Gotschy A, Manka R, Kozerke S. Quantitative three-dimensional myocardial perfusion cardiovascular magnetic resonance with accurate two-dimensional arterial input function assessment. J. Cardiovasc. Magn. Reson. 2015;17:1–11
12. Beck A, Teboulle M. A Fast Iterative Shrinkage-Thresholding Algorithm. Soc. Ind. Appl. Math. J. Imaging Sci. 2009;2:183–202
13. Uecker M, Lai P, Murphy MJ, et al. ESPIRiT - An eigenvalue approach to autocalibrating parallel MRI: Where SENSE meets GRAPPA. Magn. Reson. Med. 2014;71:990–1001
14. Vishnevskiy V, Gass T, Szekely G, Tanner C, Goksel O. Isotropic Total Variation Regularization of Displacements in Parametric Image Registration. IEEE Trans. Med. Imaging 2017;36:385–395
15. Jerosch-herold M, Wilke N, Stillman AE, et al. Magnetic resonance quantification of the myocardial perfusion reserve with a Fermi function model for constrained deconvolution Magnetic resonance quantification of the myocardial perfusion reserve with a Fermi function model for constrained deconvolution. Med. Physiol. 1998;25:73–84
16. Wissmann L, Santelli C, Segars WP, Kozerke S. MRXCAT: Realistic numerical phantoms for cardiovascular magnetic resonance. J. Cardiovasc. Magn. Reson. 2014;16
17. Engblom H, Xue H, Akil S, et al. Fully quantitative cardiovascular magnetic resonance myocardial perfusion ready for clinical use: A comparison between cardiovascular magnetic resonance imaging and positron emission tomography. J. Cardiovasc. Magn. Reson. 2017;19:1–9

Figures

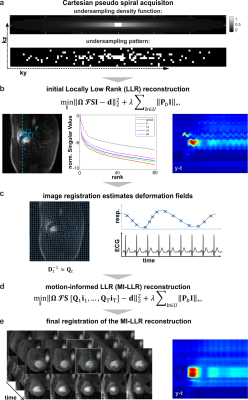
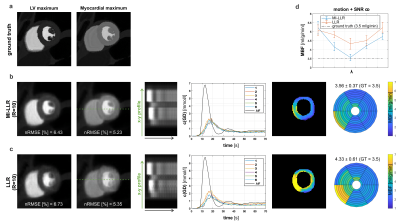
Figure 1: 3D data acquisition and reconstruction. a) Undersampling density function and 10-fold spiral-in – spiral-out pattern in the kz-/ky-domain for a single time frame with 120 samples. b) Initial local-low rank reconstruction (LLR) with indicated patches, comparison of local patch rankedness and motion profile. c) Registration of this data enables motion detection with resulting deformation field$$$\;\bf{D}_{\it{t}}$$$. Motion-informed LLR (MI-LLR) d). Final registration step results in 3D image time series and motion profile e).

Figure 2: Simulation results for synthetic stress data. Ground truth a), the motion-informed locally low-rank reconstruction (MI-LLR) b) and LLR c). For a midventricular slice, the panel shows reconstruction results and error (nRMSE) at left-ventricular (LV) and myocardial contrast maximum, x-y profile upon motion correction, concentration time curves, myocardial blood flow (MBF) maps and regional means respective MBF±STD. d) reflects the mean regional mean MBF of both algorithms for eight λ. Note that λ values are scaled and shifted to achieve minimum at the same location.

Figure 3: In-vivo results during rest condition. Motion-informed locally low-rank (MI-LLR) reconstruction magnitude image time series a), temporal profile at a midventricular slice b), mean concentration time curves over myocardial sectors with the 2D arterial input function (AIF) c), resulting myocardial blood flow (MBF) map d) and regional means e), with respective MBF±STD, are shown. For LLR reconstruction, results are depicted in (a*)-(e*), ditto.

Figure 4: In-vivo results during rest and stress condition. Stress imaging results are shown as magnitude image time series over all slices (a), temporal profile at a midventricular slice (b), mean concentration time curves over myocardial sectors with the 2D arterial input function (AIF) (c), resulting myocardial blood flow (MBF) map (d) and regional means (e) are shown, with respective MBF±STD. At rest, results are depicted in (f)-(j), ditto.

Fgure 5: Regional mean blood flows for all three volunteers at rest and stress (if applicable) and derived from the proposed motion-informed locally low-rank reconstruction (MI-LLR) and the standard LLR, respectively.

Proc. Intl. Soc. Mag. Reson. Med. 29 (2021)

0049