Introduction

MR elastography (MRE) is a non-invasive method to estimate the mechanical properties of soft tissues¹. Recording multiple phases and directions of wave propagation are always desired. However, multiphase, multi-direction MRE usually comes with an extended scan time. Several EPI or spiral based MRE sequences have been developed for acceleration^2,3, along with reconstruction methods for fast MRE imaging⁴. Recently, Strasser et al. (2019) used DENSE based encoding for multiphase MRE and showed advantages in low frequency MRE with improved acquisition efficiency⁵. In this study, we proposed a multiphase, radially sampled, DENSE based MRE sequence (MRD-MRE) for fast MRE. A reconstruction algorithm using the feature of harmonic motion and compressed sensing (CS) was also proposed.

Methods

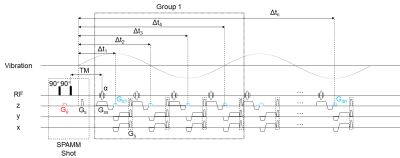
For the MRD-MRE sequence (Figure 1), the initial position of the tissue was encoded in the longitudinal magnetization with a spatial modulation of magnetization (SPAMM). Continuous vibration was triggered after the motion encoding gradient (MEG) G_e. For fast and accurate motion encoding, the initial position was encoded only once. The following motion was decoded by a decoding gradient (MDG) G_dn. Therefore, the initial phase offset could be controlled by adjusting the time interval between the trigger signal and the first MDG G_d1. Arbitrary sampling intervals for the wave propagation recording could be set by TR and the position of G_dn. The radial spokes were continuously acquired with a golden angle apart based on a gradient-echo sequence. Every 4 radial spokes within one vibration period were considered as a group. Hence, the number of groups after one SPAMM modulation determined the undersampling rate, while the amount of SPAMM shots determined the acceleration factor of the sequence.

Inspired by the iGRASP algorithm⁶, we utilized the sparsity of harmonic motion. The acquired MRE data was rearranged and concatenated through the time axis to form a pseudo continuous wave (Figure 2). Images were reconstructed by solving
$$\rm{arg}\min_x\|\bf{F}_\mit{u} \bf{Sx-y}\|\rm{_2^2} +\mit{λ}_\rm{1}\|\bf{F}^\mit{t} \rm{(}\bf{x - η\rm{)}}\|_\rm{1}+ λ_2\|\bf{TV}_\mit{hm} \rm{(}\bf{x-η}\rm{)}\|_\rm{1}$$
where $$$\bf{x}$$$ is a set of chronologically arranged images to be reconstructed, $$$\bf{y}$$$ is the acquired multi-coil k-space data, $$$\bf{F}_\mit{u}$$$ is the under-sampling scheme with a radial sampling pattern, $$$\mit{λ}_\rm{1}$$$ and $$$\mit{λ}_\rm{2}$$$ are the weighting ratios, $$$\bf{S}$$$ and $$$\bf{η}$$$ are the sensitivity maps and background noise, respectively. $$$\bf{F}^\mit{t}$$$ represents the temporal FFT, $$$\bf{TV}_\mit{hm}$$$ is a modified temporal TV transform especially for harmonic motion data, which can be described as:
$$\bf{TV}_\mit{hm} \bf{(x)} = \begin{cases}\sum\limits_{\mit{i}}\bf{x}_\mit{i}-\overline{\bf{x}_\mit{i-t}}, & \mit{i-t} > \rm{0}\\\sum\limits_{\mit{i}}\bf{x}_\mit{i}-\overline{\bf{x}_\mit{i+T-t}}, & otherwise\end{cases}$$
where $$$\mit{T}$$$ is the total number of phase images, and $$$\mit{t}$$$ denotes the sampling point interval representing one-half period.

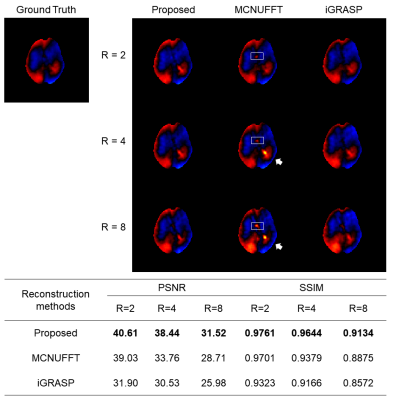
MRE images were acquired from gel phantoms and healthy volunteers. Results were compared with that from GRE and EPI based MRE using a 3T MRI scanner (uMR 790, United Imaging Healthcare, Shanghai, China). Stiffness was estimated using a local frequency estimation (LFE) algorithm^7,8. The proposed reconstruction results were compared with those from MCNUFFT and iGRASP.

Results and Discussion

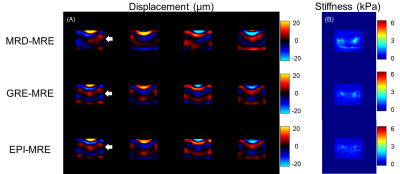
For the gel phantom with two inclusions, the recorded wavelength in the stiffer inclusion was longer (Figure 3). The MRD-MRE sequence performed better in the encoding accuracy, especially for low frequency actuation. For brain imaging, similar wave images were acquired from MRD-MRE. In addition, an acceleration factor of 4 could be achieved (25s vs. 104s).

A comparison of the reconstruction results showed the proposed reconstruction algorithm had better performance than MCNUFFT and iGRASP, with fewer artifacts of the reconstructed waveforms (Figure 5). The peak signal-to-noise ratio (PSNR) and structure similarity index (SSIM) showed the proposed method had the best performance with different acceleration factors (R = 2, 4, 8). The acceleration up to 4 folds showed satisfactory PSNR and SSIM values.

Conclusion

In this study, we proposed an MRD-MRE sequence with a harmonic motion based compressed sensing for accelerated MRE. With the modified TV transform and temporal FFT, reconstruction utilizing the sparsity of harmonic motion and compressed sensing showed the potential of further acceleration. Both the phantom and brain imaging showed the efficiency and accuracy of the proposed method.

Acknowledgements

Funding support from grant 31870941 from National Natural Science Foundation of China (NSFC) and grant 1944190700 from Shanghai Science and Technology Committee (STCSM) are acknowledged.