Introduction

Magnetic Resonance Elastography (MRE) is a novel tool to study in-vivo biomechanics for disease characterization and therapy. The diagnostic value of elasticity (dynamic modulus) has been demonstrated for the staging of liver fibrosis¹. Recently also the diagnostic value of viscosity (loss modulus) has been explored, in particular for inflammation² and tumor aggressiveness. The physical origin of viscosity is either intrinsic - constitutive thus leading to a temperature increase - or apparent - due to scattering with no concomitant increase in temperature. While viscosity at frequencies around 100Hz is significant in tissues, its physical origin - constitutive or apparent – is yet unknown. Understanding its origin will allow the correct interpretation of the observed viscosity changes and relate those to either cellular alterations (constitutive) or vascular changes (apparent), which would in turn permit therapy stratification. Loss effects lead automatically to dispersion which - in tissue - typically follows a frequency power-law. This work has two objectives: the first is to understand the origin of the loss modulus and the second is to investigate the impact of scattering on dispersion and to propose an extended theoretical model to explain the observations.

Methods

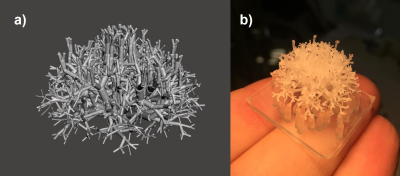
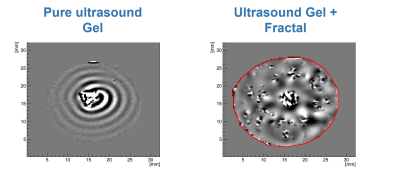
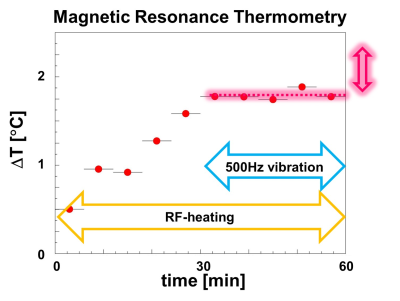
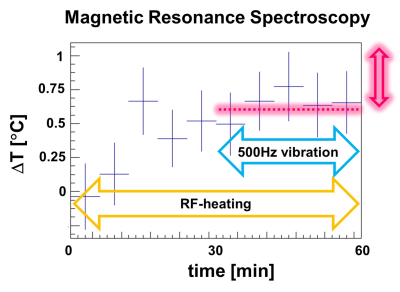
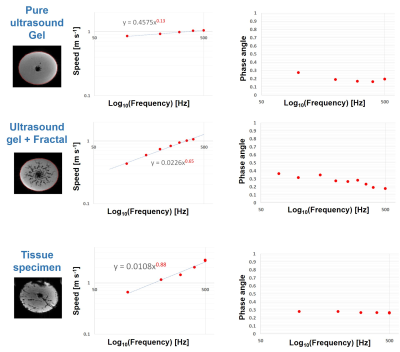
To answer the first question, an ex-vivo bovine tissue sample was exposed for 30 min to 500Hz shear vibrations with 13μm amplitude. MR-Thermometry and MR-Spectroscopy (MRT and MRS) were used to quantify tissue temperature changes over 60mins, with vibration starting after 30mins and lasting until the end of the experiment. 3D MRE @ 500Hz was also performed, measuring a loss modulus of 4kPa. Given the specific heat capacity of tissue (C=3600 J Kg^-1 K^-1), if the quantified loss modulus were entirely constitutive, a temperature increase of ~0.5°C would be expected after 30mins of vibration.
In order to investigate the impact of scattering, multi-frequency MRE (100-500 Hz) was used to study an ultrasound gel sample with/without an embedded scattering structure (Figures 1,2), as well as an ex-vivo bovine tissue sample. The structure exhibits a fractal dimension of d_f~2.3 at length scales which match the wavelength within the probed frequency bandwidth given the background stiffness of the gel (~1kPa).

Results and discussion

Figures 3 and 4 show the measured temperature increase in the bovine tissue specimen as quantified via MRT and MRS, respectively. As expected, RF-induced heating initially leads to a temperature increase of ~0.5-1°C over the first 30mins, until thermal equilibrium. Subsequently, after turning on the mechanical vibrations, no further temperature increase on the order of 0.5°C was detected! Consequently, the majority of the measured viscosity is apparent in nature, originating from scattering rather than from an intrinsic loss that would lead to a thermodynamic response. This represents a very fundamental finding which alters the way viscosity data should be interpreted. Figure 5 shows the dispersion curves and the corresponding frequency evolution of the phase angle for the pure ultrasound gel with/without fractal structure, and a bovine tissue specimen. As expected for the pure gel, the dispersion slope (0.13) and the phase angle (0.25-0.3) agree approximately (2*0.13 vs 0.25-0.3; the 2 comes from the square that converts speed to stiffness). Hence, the intrinsic dispersion of the gel can be explained via the classical springpot model that uses a fractional order time derivative to continuously interpolate between a spring (slope of stiffness equal to zero) and a dashpot (slope of stiffness equal to one).
The addition of the scattering structure dramatically changes the observations. Firstly, the measured slope of 0.65 matches what we expect from scattering theory ^3-4 with the slope approximately equal to D-d_f=3-2.3=0.7! Secondly, a slope for the speed > 0.5 entails a slope for stiffness >1, which is not explainable via the springpot model. Thirdly, while we measure a phase angle that is relatively constant in frequency, its value no longer agrees with the springpot model. Intriguingly, the results obtained for the tissue specimen are quite similar to those of the gel-embedded scattering fractal, suggesting, as observed in previous in-vitro and in-vivo results, a vasculature-generated scattering component in tissue. The observed behavior could be described by introducing a fractional order Laplacian operator in addition to the fractional order time operator of the springpot model ⁵. First, this explains slopes greater than one for the stiffness, and second, this decouples the slope from the phase angle, allowing to distinguish cellular changes (impacting intrinsic loss) from vascular alterations (changing scattering properties).

Conclusions

This work aims to uncover the origin of viscosity in tissue as quantified by MRE in the frequency range near 100Hz. We have first showed that the majority of shear viscosity is apparent, and hence originates mainly from scattering rather than from intrinsic losses. Second, we observed that the classical springpot model fails to describe the dispersion of complex media containing intrinsic scattering structures. This simplified model is incompatible with the observed dispersion of the stiffness, characterized by frequency slopes larger than one and related to the phase angle value in a more intricated manner. An extension of the springpot model using a nonlocal viscoelastic model overcomes this limitation, unveiling the ability to ultimately disentangle intrinsic/constitutive loss effects from apparent/scattering-induced ones.

Acknowledgements

This project has received funding from the National Institutes of Health (NIH) Grant Number: 1R01EB028664-01.