Multi-Coil B0 Shimming with Irregular Coil Arrays
1High-Field Magnetic Resonance, Max Planck Institute of Biological Cybernetics, Tuebingen, Germany
Synopsis
Ultra-high field (UHF) magnetic resonance imaging (MRI) enables functional brain images with sub-millimeter spatial resolution. However, susceptibility induced magnetic field (B0) variations within tissue are the source of various artifacts. Shim coils of different shape and size are applied to reduce these B0 inhomogeneity. However, most shim coils only have a regular shape and distribute current pattern on a cylinder surface or close-fit helmet. The difference in performance between current multi coil array and irregular shape multi coil array has not been explored. The optimization methods for multi-coil shim arrays are discussed, together with design and construction procedure.
Target Audience:
Ph.D. candidates and aboveIntroduction
Ultra-high magnetic field strength provides several advantages, including much improved T2* contrast and image signal-to-noise ratio (SNR). These advantages can be exploited by acquiring data with reduced voxel sizes to produce sub-millimeter spatial resolution. UHF MRI suffered from an inherent limitation: off-resonance scales with the magnetic field strength. Accordingly, susceptibility artifacts are worse in UHF MRI than at lower field strength.Shim coils are used to reduce B0 inhomogeneities by generating a compensating field to counteracts the off-resonance field. In practice, this can be done by whole-body spherical harmonic (SH) shimming, which generates a magnetic field with the spatial distribution described by spherical harmonic functions up to the second or the third order (Eq.1)(1). While being useful, SH shimming cannot effectively improve locally confined field inhomogeneity, where the required number of shim coils and the SH order are high (2, 3). Alternatively, multi-coil shim array using multiple small shim coils around the imaging object might be applied (3). The generated local fields can contribute effectively to counteract the existing B0 inhomogeneity. Such coils feature low inductance and small size which is advantageous to dynamic slice-wise shimming (4, 5), integration into the RF receive coil (6, 7), real-time correction of temporal B0 alteration (8), generating spatial encoding magnetic fields (9), and novel parallel imaging methods (10).
$$∆B_0 (x,y,z)=B_{0,offset}+\sum_{I=0}^∞\sum_{m=-I}^{+I}C_{I,m}F_{I,m}(x,y,z)\space\space{(I)}$$
Multi-coil shim arrays and integrated RF/B0 shim coil arrays (6, 7) typically have a simple shape, for instance, a circular loop distributed in a regular pattern on a cylinder surface or close-fitting helmet. Previous simulations demonstrate that increasing the number of coils goes along with improved shimming capability (7), since more shim coils provide higher degree of freedom in shim current design. In parallel, the increasing number of coils would require extra amplifiers and consume more space within the bore. Furthermore, difficulties in maintenance and troubleshooting are expected.
In the brain region, the major field inhomogeneities are found near air-tissue boundary, for instance, in prefrontal cortex and temporal lobe. Given the similarity of human anatomy structure and the pattern of B0 inhomogeneity in the human brain. Therefore, the shim array can be modified for better performance on an identified target pattern. Previous studies placed the active shim coils in the mouth (11) or over the nose (12, 13) to improve B0 uniformity in the frontal lobe. Another study use genetic algorithm to optimize a shim coil with irregular shape for 4 representative brain slices (14) and extended later for optimizing position and geometry of 16 channel multi-coil array for 2 brain slices (15).
Here we present two methods for the design of multi-coil shim arrays at ultra-high field. Shim arrays are optimized to targeting the whole-brain B0 inhomogeneity, while keeping the shim coil number in a reasonable range and feasible for in-house construction
1. Nonlinear constrained optimization for coil size and position (16)
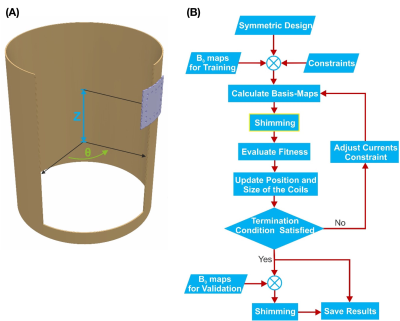
Started from a symmetric 32 channel multi-coil array on the cylinder surface. The coil element had an identical square shape with a side length of 60 mm and 25 turns. We optimize 3 DOFs of each coil (Figure 1A):1) The size, i.e. side length. Constrained between [20 100] mm
2) Axial coordinate (Z) of the coil’s center on the cylinder surface. Constrained between [-150 80] mm
3) Angular coordinate (θ), the angle between the reference axis on a chosen plane and a line from the origin to the projection of the coil center to that plane.
Unconstrained We use a nonlinear constrained optimization function, fmincon, in MATLAB (MathWork, Inc. Natick, MA, USA). The flowchart of the optimization process is depicted in Figure 1B. First, we use a group of 8 B0 maps for training. Within iteration, the position and size were estimated numerically by the gradient of a cost function (Eq. 2), which was defined as the sum of the residual magnetic field of 8 training data, using sequential quadratic programming (SQP):$$cost(τ)= \sum_{i=1}^{8}\sum_{j=1}^{32}(C_{ij}F_j(x,y,z)+B_i(x,y,z))\space\space(II)$$ ,where τ includes the size and position of the coils in the current iteration, Bi is the B0 map of the ith brain, CijFj is the magnetic field created by the shim coils for ith brain. The current of each coil was determined by a constrained least-squares optimization, with a variable boundary from 1.5A to 3A according to the coil size. The optimization will be terminated when the changes in the position and size of the coils are smaller than a defined threshold.
2. Stream function method(17)
The current density on a surface is obtained from a stream function by taking the curl:$$J(r_n )= ∇×[ψ(r_n)n(r_n)]\space\space(III)$$
The shim coil design begins by defining two components(18): (a) a conductor shim coil surface S where current flows, and (b) a region of interest (ROI) V, in this case a group of 84 (12 subjects * 7 positions) field maps. The local shim coil surface orientation is given by its normal vector at a given location . In general, the coil surface consists of various sub-surfaces and sub regions. Here we use cylinder geometry.
In order to obtain a physically and technically meaningful solution, the power dissipated by the shim coil was constrained using cgsvd and lsqi in the MATLAB.
The final wire pattern of shim coil array was obtained using singular values decomposition (SVD) method. After solving the stream function for all training field maps, a n*m matrix was formed. Where n indicates the total number of nodes on the mesh and m corresponds to the total number of field maps entering the basis generation algorithm. The resulting singular vectors were used to obtain the wire pattern of coil elements of a shim coil array.
Acknowledgements
The author would like thank Ali Aghaeifar, Feng Jia, Jason Stockmann and Bruno Pinho-Meneses for helpful documents. This work was supported by DFG SCHE658/13 and the Max Planck Society.
References
1.RA de Graaf,C Juchem. CHAPTER 4 B0 Shimming Technology. Magnetic Resonance Technology: Hardware and System Component Design: The Royal Society of Chemistry; 2016. p 166-207.
2.C Juchem, S Umesh Rudrapatna, TW Nixon,RA de Graaf. Dynamic multi-coil technique (DYNAMITE) shimming for echo-planar imaging of the human brain at 7 Tesla. Neuroimage 2015;105:462-72.
3.C Juchem, TW Nixon, S McIntyre, DL Rothman,RA de Graaf. Magnetic field modeling with a set of individual localized coils. J Magn Reson 2010;204(2):281-9.
4.C Juchem, TW Nixon, S McIntyre, VO Boer, DL Rothman,RA de Graaf. Dynamic multi-coil shimming of the human brain at 7 T. J Magn Reson 2011;212(2):280-8.
5.A Aghaeifar, C Mirkes, J Bause, T Steffen, N Avdievitch, A Henning,K Scheffler. Dynamic B0 shimming of the human brain at 9.4 T with a 16-channel multi-coil shim setup. Magn Reson Med 2018.
6.TK Truong, D Darnell,AW Song. Integrated RF/shim coil array for parallel reception and localized B0 shimming in the human brain. Neuroimage 2014;103:235-40.
7.JP Stockmann, T Witzel, B Keil, JR Polimeni, A Mareyam, C LaPierre, K Setsompop,LL Wald. A 32-channel combined RF and B0 shim array for 3T brain imaging. Magn Reson Med 2016;75(1):441-51.
8.Topfer R, Foias A, Stikov N, Cohen‐Adad J. Real‐time correction of respiration‐induced distortions in the human spinal cord using a 24‐channel shim array. Magn Reson Med. 2018;80:935–946.
9.Umesh Rudrapatna S, Fluerenbrock F, Nixon TW, de Graaf RA, Juchem C. Combined imaging and shimming with the dynamic multi‐coil technique. Magn Reson Med. 2019;81:1424–1433
10.Scheffler K, Bause J, Loktyushin A, Aghaeifar A, Steffen T, Schölkopf B. Spread‐spectrum magnetic resonance imaging. Magn Reson Med. 2019;82:877–885.
11.JJ Hsu,GH Glover. Mitigation of susceptibility-induced signal loss in neuroimaging using localized shim coils. Magn Reson Med 2005;53(2):243-8.
12.C Juchem, TW Nixon, S McIntyre, DL Rothman,RA de Graaf. Magnetic field homogenization of the human prefrontal cortex with a set of localized electrical coils. Magn Reson Med 2010;63(1):171-80.
13.J Zhou, JP Stockmann, N Arango, T Witzel, K Scheffler, LL Wald,FH Lin. An orthogonal shim coil for 3T brain imaging. Magn Reson Med 2020;83(4):1499-1511.
14.Zivkovic I, Mirkes C, Scheffler K. B0 shimming at 9.4T using a multi‐coil approach—coil design with genetic algorithm. In 24th Annual Meeting and Exhibition of the ISMRM, Singapore, 2016. p. 1152.
15.Zivkovic I, Tolstikhin I, Schölkopf B, Scheffler K. B0 matrix shim array design‐optimization of the position, geometry and the number of segments of individual coil elements. In 33rd Annual Scientific Meeting of the European Society for Magnetic Resonance. Medicine and Biology. Vienna, Austria, 2016:36.
16.A Aghaeifar, J Zhou, R Heule, B Tabibian, B Schölkopf, F Jia, M Zaitsev,K Scheffler. A 32‐channel multi‐coil setup optimized for human brain shimming at 9.4T. Magnetic Resonance in Medicine 2019;83(2):749-764.
17.F Jia, H Elshatlawy, A Aghaeifar, YH Chu, YC Hsu, S Littin, S Kroboth, H Yu, P Amrein, X Gao, W Yang, P LeVan, K Scheffler,M Zaitsev. Design of a shim coil array matched to the human brain anatomy. Magn Reson Med 2020;83(4):1442-1457.
18.Peeren GN. Stream function approach for determining optimal surface currents. J Comput Phys. 2003;191:305–321
Figures