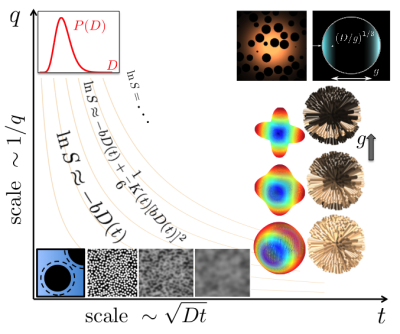
This talk begins as an excursion in the landscape of diffusion weighted signal in the plane formed by the wave vector $$$q$$$ and diffusion time $$$t$$$ [1,2], Fig.1. Limiting the consideration to this plane is a large simplification, only exact in the limit of narrow gradient pulses in which the signal is the Fourier-transformed sample-average diffusion propagator [3]. In the spirit of this relation, a researcher measuring diffusion with a given $$$q$$$ anticipates the sensitivity to the spatial scale $$$1/q$$$, which can be called the default approach. The probed scale will be discussed in more detail below in the context of different measurement techniques. For measurements with long gradient pulses, the sensitivity to the tissue microstructure is specified by the complete time course of a diffusion-weighting gradient $$${\vec g}(t)$$$ with $$$\vec q(t)$$$ being its antiderivative. Both $$$q$$$ and $$$t$$$ in the image should be understood as order-of-magnitude representatives of the detailed function $$$\vec g(t)$$$.

The excursion begins in the corner of small $$$q$$$ and short times. From that point, we see a downslope labelled with the contour lines of the so-called b-value (or b-factor) [4]. These lines show the uncertainty in $$$t$$$ and $$$q$$$, which is essential for measurements in structured media.

We start descending from the highest point in the direction of increasing time keeping the diffusion-weighing gradient small. In this limit, the signal is only sensitive to the diffusion tensor. For short diffusion times, the decrease in $$$D(t)$$$ reveals the total surface of impermeable interfaces in a unit volume of the medium [5]. The question about the scale is answered in the negative form: The measurement is insensitive to the curvature of impermeable interfaces up to small corrections [6]. This technique has been applied to evaluation of the size of prostate lumens [7].

Moving further along the time axis, we note that for a given diffusion time, the typical displacement of molecules is of the order of $$$\sqrt{Dt}$$$. This makes the medium structure increasingly blurred as seen by diffusing molecules, the process called the coarse-graining in physics, which is illustrated with a series of images of a granular two-dimensional medium in Fig.1. It manifests itself in a power-law approach of the diffusion coefficient to its long-time asymptote with the exponent reflecting the effective dimensionality of diffusion and the statistics of long-distance correlations of restrictions on the scale $$$\sqrt{Dt}$$$ [8]. This process has been observed in the normal human brain white matter revealing effectively one-dimensional diffusion [9].

The diffusion length $$$\sqrt{Dt}$$$ is the ``native" scale of a measurement, which means that the signal is sensitive to this scale without any additional suppression. For an NMR measurement, we need values of $$$q$$$ inversely proportional to the coarse-graining length, $$$\sqrt{Dt}$$$. From the practical point of view, this requirement implies a noticeable, but not too strong signal attenuation when $$$bD \sim Dtq^2 \sim 1$$$.

Turning up to go along the $$$q$$$ axis leads further downhill, according to the signal reduction for stronger gradients. By descending from the origin along the $$$q$$$ axis, we come to the domain of short times and strong gradients. In this regime, the signal is simply $$$\langle \exp(-bD) \rangle$$$ where the averaging is performed over the distribution of $$$D$$$ in the sample [10]. The signal does not refer to a definite spatial scale, but one has to realize that $$$D$$$ in the above expression is already averaged on all scales below $$$\sqrt{Dt}$$$ and this length should be much smaller than any other characteristic length in the medium.

Moving parallel to the $$$q$$$ axis for long diffusion times brings us in the park of currently popular models of brain white matter as multiple Gaussian compartments [11,2]. The biological compartments are nearly Gaussian when $$$\sqrt{Dt} \gg \ell_c$$$, where $$$\ell_c$$$ is the correlation length of diffusion heterogeneity in the medium (e.g. the cell size). The models are illustrated with the glyphs showing the increase in the angular resolution of crossing fibers with increasing $$$q$$$, which are largely used for fiber tracking. As it follows from the cumulant expansion, the terms up to the order $$$q^n$$$ contain contributions of spherical harmonics up to the order $$$\ell = n$$$ [12,13,2]. Another set of images illustrates the model of white matter fibers as straight homogeneous cylinders, which are shown with a common origin to focus on their orientation distribution. With the increasing $$$q$$$, less axons contribute to the powder-averaged signal (light color), which results in the observed signal decrease in proportion to $$$1/\sqrt{b}$$$ [14,15,16,17]. For both examples, the probed orientation distribution does not refer to a specific length. However, diffusion length enters the result implicitly by defining the length of axons over which they should be effectively straight. The axon diameter falls out being too small for typical measurements requiring much larger gradients for its detection [8,16], but can be marginally detected by its contribution in the deviation from the $$$1/\sqrt{b}$$$ signal attenuation [17].

The upper right corner of the map contains a swiss-cheese-like image illustrating a possibility to access the correlation function of a porous medium [5]. Such a medium is shaped by excluded volume of a complex geometry, typically NMR-invisible (e.g. porous rock) filled with an NMR-visible fluid (e.g. water) forming a single connected compartment with complex geometry. The key idea is that the diffusion propagator has the form of a nearly Gaussian envelope with a fine structure imprinted by the excluded volume. The signal acquired in this regime is a convolution of a Gaussian propagator, $$$\exp(-Dtq^2$$$) with the medium correlation function. In this way, we access the scale of the medium correlation length, $$$\ell_c \ll \sqrt{Dt}$$$. The price for that is the suppression of the informative part of the signal by the factor $$$(\ell_c/\sqrt{Dt})^d$$$ in $$$d$$$ spatial dimensions.

The plane shown in Fig.1 cannot encompass all possible measurements. Consider the Stejskal -- Tanner pulse sequence with a finite gradient pulses duration $$$\delta$$$ and the interpulse interval $$$\Delta\geq \delta$$$. The diffusion time is not well defined, but can be estimated as $$$t\sim \Delta$$$. In the following two examples, long $$$\delta\sim t$$$ is crucial for the measurement outcome. Consider an NMR-visible fluid with the diffusivity $$$D_0$$$ confined in a closed compartment with the size $$$a$$$, The true diffusion coefficient defined via the mean squared displacement of molecules is $$$D(t)\sim a^2/t$$$ for long diffusion times, $$$\sqrt{D_0 t}\gg a$$$, independent of $$$D_0$$$. The signal attenuation measured with short gradient pulses is $$$\ln S\sim -q^2a^2$$$, from which the value of $$$D(t)$$$ can be obtained correctly. This changes for long, constantly applied gradient for which the signal attenuation is $$$\ln S \sim -g^2a^4 t/D_0$$$ [18,19]. This is the factor $$$a^2/(D_0 t) \ll 1$$$ smaller than for the narrow gradient pulses if we estimate $$$q\sim gt$$$. The same factor compromises an attempt to find $$$D(t)$$$ via the division by the b-value, $$$b\sim q^2t$$$.

Another example is symbolized in the upper right corner in Fig.1. It is the so-called localization regime [20,21,22]. In this regime, the major signal comes from layers adjacent to impermeable interfaces with the thickness about $$$(D/g)^{1/3} \ll \sqrt{Dt}$$$. In contrast to the previous example, application of long gradient pulses suppresses the signal exponentially as $$$\ln S \sim - (bD)^{1/3}$$$. This signal is much smaller than for the narrow gradient pulses for which $$$S\sim 1/q^2$$$ in three dimensions (the diffusion diffraction, [23]). Strictly speaking, this image does not belong the $$$(q,t)$$$ plane. it is rather a projection from the third direction of final $$$\delta$$$, which is not shown in Fig.1.

Nor can numerous methods of combining gradient pairs be shown in Fig.1. These methods can be loosely considered as successors of the double-diffusion encoding [24,25] (going to the continuum limit for the constantly rotated gradients [26,27,28]). The unifying idea of those methods can be called the ``geometry matching", that is suppressing some compartments to measure more specifically other ones using the difference in their shape. For example, the spherical encoding (or isotropic weighting) is used to suppress the signal from everything except for the small compact cells (the dot compartment) with the aim to evaluate their weight in the total signal [29,30]. Another example is the use of planar weighting to narrow the native orientation distribution of white matter axons and suppress the signal from other cells [31].

Note that exchange between tissue compartments is a serious confounding factor for the presently available microstructure modeling. In some cases, it is slow enough to enable the approximation of non-exchanging compartments, but not always. The next talk is focused on this issue.

Acknowledgements

I am grateful to Dmitry S. Novikov for stimulating discussions.

References

[1] Valerij G Kiselev. Fundamentals of diffusion MRI physics. NMR Biomed, 30(3):e3602, Mar 2017. [2] Dmitry S Novikov, Els Fieremans, Sune N Jespersen, and Valerij G Kiselev. Quantifying brain microstructure with diffusion MRI: Theory and parameter estimation. NMR Biomed, 32(4):e3998, Oct 2018. [3] Paul T Callaghan. Principles of nuclear magnetic resonance microscopy. Oxford University Press Inc., New York, 1991. [4] D Le Bihan, E Breton, D Lallemand, P Grenier, E Cabanis, and M LavalJeantet. Mr imaging of intravoxel incoherent motions: application to diffusion and perfusion in neurologic disorders. Radiology, 161(2):401–7, Nov 1986. [5] P. P. Mitra, P. N. Sen, L. M. Schwartz, and P. Le Doussal. Diffusion propagator as a probe of the structure of porous media. Physical Review Letters, 68(24):3555–3558, 1992. [6] P. P. Mitra, P. N. Sen, and L. M. Schwartz. Short-time behaviour of the diffusion coefficient as a geometrical probe of porous media. Phys. Rev. B, 47 (14):8565–8574, 1993. [7] Gregory Lemberskiy, Els Fieremans, Jelle Veraart, Fang-Ming Deng, Andrew B. Rosenkrantz, and Dmitry S. Novikov. Characterization of prostate microstructure using water diffusion and NMR relaxation. Frontiers in Physics, 6:91, 2018. [8] Dmitry S Novikov, Jens H Jensen, Joseph A Helpern, and Els Fieremans. Revealing mesoscopic structural universality with diffusion. Proc Natl Acad Sci U S A, 111(14):5088–93, Apr 2014. [9] Els Fieremans, Lauren M Burcaw, Hong-Hsi Lee, Gregory Lemberskiy, Jelle Veraart, and Dmitry S Novikov. In vivo observation and biophysical interpretation of time-dependent diffusion in human white matter. Neuroimage, 129:414–27, Apr 2016. [10] Dmitriy A. A. Yablonskiy, G. L. Bretthorst, and Joseph J H Ackerman. Statistical model for diffusion attenuated MR signal. Magn Reson Med., 50:664–669., 2003. [11] Dmitry S Novikov, Valerij G Kiselev, and Sune N Jespersen. On modeling. Magn Reson Med, 79(6):3172–3193, Jun 2018. [12] Valerij G. Kiselev. The cumulant expansion: An overarching mathematical framework for understanding diffusion NMR. In Derek K Jones, editor, Diffusion MRI: Theory, Methods and Applications, chapter 10, pages 152– 168. Oxford University Press, New York, 2010. [13] Dmitry S Novikov, Jelle Veraart, Ileana O Jelescu, and Els Fieremans. Rotationally-invariant mapping of scalar and orientational metrics of neuronal microstructure with diffusion MRI. Neuroimage, 174:518–538, Jul 2018. [14] Christopher D. Kroenke, Joseph J. H. Ackerman, and Dmitriy A. Yablonskiy. On the nature of the NAA diffusion attenuated MR signal in the central nervous system. Magn Reson Med, 52:1052–1059, 2004. [15] Emilie T McKinnon, Jens H Jensen, G Russell Glenn, and Joseph A Helpern. Dependence on b-value of the direction-averaged diffusionweighted imaging signal in brain. Magn Reson Imaging, 36:121–127, Feb 2017. [16] Jelle Veraart, Els Fieremans, and Dmitry S Novikov. On the scaling behavior of water diffusion in human brain white matter. NeuroImage, 185:379– 387, Jan 2019.[17] Jelle Veraart, Daniel Nunes, Umesh Rudrapatna, Els Fieremans, Derek K Jones, Dmitry S Novikov, and Noam Shemesh. Noninvasive quantification of axon radii using diffusion mri. eLife, 9:e49855, feb 2020. [18] C. H. Neuman. Spin echo of spins diffusing in a bounded medium. Journal of Chemical Physics, 60(11):4508–4511, June 1974. [19] P van Gelderen, M H de Vleeschouwer, D DesPres, J Pekar, P C van Zijl, and C T Moonen. Water diffusion and acute stroke. Magn Reson Med, 31(2):154–163, Feb 1994. [20] FD Stoller, W Happer, and FJ Dyson. Transverse spin relaxation in inhomogeneous magnetic fields. Phys Rev A, 44(11):7459–7477, Dec 1991. [21] M.D. Hurlimann, K.G. Helmer, T.M. Deswiet, and P.N. Sen. Spin echoes in a constant gradient and in the presence of simple restriction. Journal of Magnetic Resonance, Series A, 113(2):260 – 264, 1995. [22] Nicolas Moutal, Kerstin Demberg, Denis S Grebenkov, and Tristan Anselm Kuder. Localization regime in diffusion NMR: Theory and experiments. J Magn Reson, 305:162–174, Aug 2019. [23] P. T. Callaghan, A. Coy, D. Macgowan, K. J. Packer, and F. O. Zelaya. Diffraction-like effects in NMR diffusion studies of fluids in porous solids. Nature, 351(6326):467–469, 1991. [24] Partha P Mitra. Multiple wave-vector extensions of the NMR pulsed-fieldgradient spin-echo diffusion measurement. Phys Rev B Condens Matter, 51(21):15074–15078, Jun 1995. [25] Noam Shemesh, Sune N Jespersen, Daniel C Alexander, Yoram Cohen, Ivana Drobnjak, Tim B Dyrby, Jurgen Finsterbusch, Martin A Koch, Tristan Kuder, Fredrik Laun, Marco Lawrenz, Henrik Lundell, Partha P Mitra, Markus Nilsson, Evren O ̈zarslan, Daniel Topgaard, and Carl-Fredrik Westin. Conventions and nomenclature for double diffusion encoding NMR and MRI. Magn Reson Med, 75(1):82–7, Jan 2016. [26] Stefanie Eriksson, Samo Lasic, and Daniel Topgaard. Isotropic diffusion weighting in PGSE NMR by magic-angle spinning of the q-vector. Journal of Magnetic Resonance, 226:13 – 18, 2013. [27] Samo Lasiˇc, Filip Szczepankiewicz, Stefanie Eriksson, Markus Nilsson, and Daniel Topgaard. Microanisotropy imaging: quantification of microscopic diffusion anisotropy and orientational order parameter by diffusion MRI with magic-angle spinning of the q-vector. Frontiers in Physics, 2:11, 2014. [28] Filip Szczepankiewicz, Samo Lasiˇc, Danielle van Westen, Pia C Sundgren, Elisabet Englund, Carl-Fredrik Westin, Freddy St ̊ahlberg, Jimmy L ̈att, Daniel Topgaard, and Markus Nilsson. Quantification of microscopic diffusion anisotropy disentangles effects of orientation dispersion from microstructure: applications in healthy volunteers and in brain tumors. Neuroimage, 104:241–52, Jan 2015. [29] Bibek Dhital, Elias Kellner, Valerij G Kiselev, and Marco Reisert. The absence of restricted water pool in brain white matter. Neuroimage, 182:398– 406, Nov 2018. [30] Chantal M.W. Tax, Filip Szczepankiewicz, Markus Nilsson, and Derek K. Jones. The dot-compartment revealed? Diffusion MRI with ultra-strong gradients and spherical tensor encoding in the living human brain. Neuroimage, 210:116534, Apr 2020. [31] Bibek Dhital, Marco Reisert, Elias Kellner, and Valerij G Kiselev. Intraaxonal diffusivity in brain white matter. NeuroImage, 189:543–550, Jan 2019.